2025秋 2024秋 课程号：COMP6001P02
- 课程难度：困难
- 作业多少：中等
- 给分好坏：一般
- 收获大小：一般
| 选课类别：基础 | 教学类型：理论课 |
| 课程类别：研究生课程 | 开课单位：计算机科学与技术系 |
| 课程层次：硕士 | 学分：3.0 |
算法设计与分析是计算机科学与技术各专业硕士研究生必修的基础课。本课程主要介绍概率算法、近似算法和分布式算法基础，使学生掌握概率算法、近似算法和分布式算法设计及分析的基本方法。主要内容分为如下三个部分。
一. 概率算法，主要包括：
1．基本概念：主要介绍概率算法的特点、意义、分类、复杂性分析方法；2．数字概率算法：重点介绍π值计算、数值积分、概率计数以及其它数值算法的设计和分析；3．Sherwood算法：以选择和排序、随机预处理、有序表搜索等问题为例重点介绍Sherwood算法的概念和特点，以及算法设计和分析的方法；4．Las Vegas算法：以n－皇后、模p平方根、整数的因式分解等问题为例重点介绍Las Vegas算法的概念和特点，以及算法设计和分析的方法；5．Monte Carlo算法：重点介绍一致、有偏、精度分析等基本概念，以主元素、素性判定、矩阵相乘等问题为例，重点介绍Monte Carlo算法设计、分析和改进的方法。
二、近似算法，主要包括：
1．NP完全性理论：主要介绍图灵机等计算模型、问题变换及计算复杂性规约、P类问题、NP类问题、NP-hard和NPC问题、Cook定理等；2.基本概念：介绍优化问题的近似解分类、近似算法的绝对性能保证、相对性能保证（包括绝对性能比、渐近性能比、最佳可达性能比）、近似模式（多项式近似模式、完全多项式近似模式）、绝对近似算法之否定、相对近似算法之否定等；3.基本算法：图的顶点着色、图的边着色、多机调度、装箱、旅行商、顶点覆盖和最大独立集问题等问题的近似算法。
三、分布式算法基础，主要包括：
1．基本概念：介绍分布式系统、计算模型、复杂性度量标准等分布式计算的基本概念；2．分布式算法基础：主要介绍同步和异步网络模型，同步/异步环中的Leader选举、一般网络中的Leader选举、生成树构造、广播和敛播、广度/深度优先搜索、最短路径、最大独立集等分布式算法；介绍异步共享存储器和网络算法、重点介绍互斥和资源分配问题，介绍哲学家用餐算法、着色算法、有向无环图算法以及哲学家饮水算法等。
教学内容与水平
课程内容相对抽象，实用性有限。PPT内容多年未更新，部分错误和语病未修正，阅读困难。课程资料获取较容易，适合考前突击，但实际理解难度较大。
考试与难度
考试难度较高，题目变化明显，大题尤其困难。大部分题目与授课内容关系不大，有些考题描述不够清晰。考试有考学分离现象，造成复习时间长短影响不大。选择题相对正常，但大题设计被认为较偏。
作业负担
作业不多且较为简单，随便写写即可，课程不点名，平时压力相对较小。
给分与调分
总评给分慷慨，多数学生获得高分，这被认为是调分的结果。即使考试部分内容未答出，最终成绩仍然不错，事实上很多同学获得90分以上的总评。
总体来说，虽然考试和教学内容难度较高，但优良的给分制度导致最终成绩较高。这门课程适合那些对计算机科学有浓厚兴趣且想挑战自己的同学，也适合希望通过突击复习获得高分的学生。
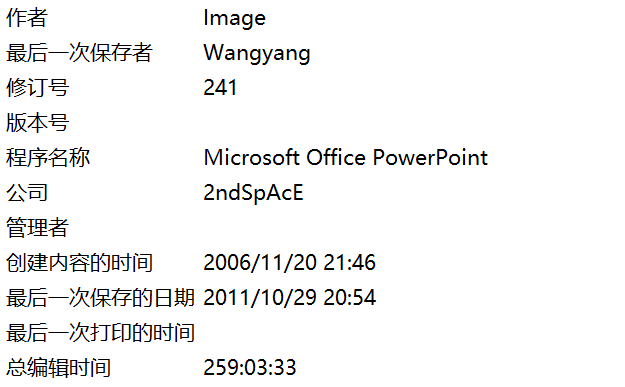
2006年创建的ppt，那一年，这门课的某些学生可能还没出生吧。2011年，最后一次修改，那一年大多数同学应该是上小学没多久。重读这份ppt，一想到我的导师，甚至可能我导师的导师也对着一模一样的东西抓耳挠腮，我不禁感受到一种历史的厚重感。
Apple II机器，真是让人深受触动。中科大真是注重传承，即使近50年后的今天还要带大家回望科大南迁合肥，乔布斯在车库创业的那段岁月。泪眼婆娑的我看向了我的桌面，天哪，我的充电线，你的算力怎么是我们算法课件上拿来跑n皇后的机器的50倍啊？
- 课程难度：困难
- 作业多少：中等
- 给分好坏：一般
- 收获大小：一般
- 难度：困难
- 作业：中等
- 给分：一般
- 收获：一般
黑色和黄色混在一起是什么呢？哦原来是PPT啊，我还以为是shi呢🤓
- 课程难度：困难
- 作业多少：中等
- 给分好坏：一般
- 收获大小：一般
- 难度：困难
- 作业：中等
- 给分：一般
- 收获：一般
考学分离，无敌了
据说是汪老师出题，结果连肖老师教了哪些内容都不知道就摁出题，有几道概率、近似算法题出现了超纲的概念，你看看这出的啥？
30分的算法设计，4问，除了最后一问，其余几问根部不涉及到本门课程所学内容。但是最后一题太难，估计很多同学做不到第4问，也就是说复习一周的同学大概率和复习2天的同学拿一样分，这30分的题目意义何在我请问呢？
不过课程确实是有收获的，我只能说考学分离属实恶心，三分吧
- 课程难度：中等
- 作业多少：中等
- 给分好坏：一般
- 收获大小：一般
- 难度：中等
- 作业：中等
- 给分：一般
- 收获：一般
一个字都看不懂，一个字都看不懂，一个字都看不懂，鲨了我吧，鲨了我吧，鲨了我吧
二编，抄作业呢，为什么研究生课都不愿意发习题课ppt呢，把它那答案当个宝
来祈祷喽
我的flooding呢 我的最小顶点覆盖呢 我的leadr的LV算法呢 痛苦
过了 但这一门考学分离的课，我实在是难评
- 课程难度：困难
- 作业多少：很少
- 给分好坏：一般
- 收获大小：没有
- 难度：困难
- 作业：很少
- 给分：一般
- 收获：没有
真的是好难好难好难好难，复习过程太煎熬了，ppt没有几个字能读懂。。。。。等一个助教和老师捞捞吧真的尽力了。。。。。😭😭😭😭😭
- 课程难度：中等
- 作业多少：中等
- 给分好坏：一般
- 收获大小：一般
- 难度：中等
- 作业：中等
- 给分：一般
- 收获：一般
还是理解不了jwc把一个十几年授课内容几乎不变的课程在2025年设置成为电子信息专硕的必修课的意义在哪。。。
- 课程难度：困难
- 作业多少：中等
- 给分好坏：超好
- 收获大小：一般
- 难度：困难
- 作业：中等
- 给分：超好
- 收获：一般
大学生涯中第一门考完了虽然感觉要挂但是如释重负的课。复习备考太痛苦了，PPT 简直不讲人话，看 PPT 犹如完形填空，仿佛回到了啃代数结构课本的那些日子，并且十几年过去了 PPT 里面一些错误和语病都没想着修正一下；对着往年卷子过拟合后拿到考卷发现30%重合度都没有，气笑了。
给分挺好，上调几分
- 课程难度：困难
- 作业多少：中等
- 给分好坏：一般
- 收获大小：没有
- 难度：困难
- 作业：中等
- 给分：一般
- 收获：没有
今年相较于往年题目变化巨大，原题不多，感觉很多地方都是疏忽的地方，对突击考试的同学不太友好（大佬除外），做了很多套往年的卷子，感觉都没派上用场，求求老师捞一捞了，不知道会不会调分。。。。。。
- 课程难度：困难
- 作业多少：中等
- 给分好坏：超好
- 收获大小：一般
- 难度：困难
- 作业：中等
- 给分：超好
- 收获：一般
如果不是必选不可能碰的课，非常抽象，ppt和十年前相比完全没变化，考试也非常离谱。等出分了再来评价一次。
出分了，89，被狠狠捞了一把，上调一颗星，不过依旧不推荐
- 课程难度：困难
- 作业多少：中等
- 给分好坏：超好
- 收获大小：一般
- 难度：困难
- 作业：中等
- 给分：超好
- 收获：一般
人都麻了，大题一个不会搁那瞎编（关键简答题ppt上也没有啊，算法题更是无敌不知道和这课有什么关系，只填了前两问），50分都悬
看助教在群里说平时分占比≈50%，等一个捞人，出分了再回来评
给分超好，这都能给我捞出来，牛的
- 课程难度：困难
- 作业多少：中等
- 给分好坏：超好
- 收获大小：一般
- 难度：困难
- 作业：中等
- 给分：超好
- 收获：一般
难度很高，学的内容实用性有限。不过作为一门古早课程，资料获取十分容易，适合平时水最后突击。给分暂不清楚，等更新。
新鲜出炉的个人回忆版试题：25秋试卷回忆版.txt
- 课程难度：中等
- 作业多少：中等
- 给分好坏：一般
- 收获大小：一般
- 难度：中等
- 作业：中等
- 给分：一般
- 收获：一般
一学期只去过第一节课，打瓦打到考前两天的清晨六点，课程ppt强如怪物，拼尽全力无法战胜🤪
看到大伙的评论，庆幸只预习了两天(
- 课程难度：困难
- 作业多少：很少
- 给分好坏：超好
- 收获大小：一般
- 难度：困难
- 作业：很少
- 给分：超好
- 收获：一般
考试跟往年题有较大变化，大题对分布式算法的考察较少（吐槽：不是汪老师出题嘛），而且有点偏，个别题目的描述有些令人困惑。
算法设计题是求一个概率，我是用数值MC算法写的。
简答题写的不是很好，给分还不错。
分布式算法的黑底黄字上古ppt略显阴间了，内容也很晦涩难懂。
- 课程难度：困难
- 作业多少：中等
- 给分好坏：超好
- 收获大小：一般
- 难度：困难
- 作业：中等
- 给分：超好
- 收获：一般
- 课程难度：困难
- 作业多少：中等
- 给分好坏：超好
- 收获大小：一般
- 难度：困难
- 作业：中等
- 给分：超好
- 收获：一般
期末大题挺难的，五个我只写了两个半，最后被海底捞上来了，what can i say
- 课程难度：困难
- 作业多少：中等
- 给分好坏：超好
- 收获大小：没有
- 难度：困难
- 作业：中等
- 给分：超好
- 收获：没有
三次作业随便写写就行，课程不点名，主要复习太痛苦了，对着不是人话的PPT看了一周头都大了，不过最后给分很好
- 课程难度：中等
- 作业多少：中等
- 给分好坏：一般
- 收获大小：没有
- 难度：中等
- 作业：中等
- 给分：一般
- 收获：没有
课程难度在近似算法之前还好。
考试考得比较tricky。选择题很正常，但大题一言难尽。尤其是最后一道大题出的那道30分的算法设计题，一眼看是十分典型的dp题（我没想到怎么用概率或者近似的做法去优化DP）
最后给分相当不错，考试后面大题基本都没复习到，最后一道题就糊了个DP上去，最后能有89的总评
- 课程难度：简单
- 作业多少：很少
- 给分好坏：超好
- 收获大小：没有
- 难度：简单
- 作业：很少
- 给分：超好
- 收获：没有
居然有88分，也是神人了。试卷一半的题不会做，调分也是神人了。
- 课程难度：困难
- 作业多少：中等
- 给分好坏：杀手
- 收获大小：没有
- 难度：困难
- 作业：中等
- 给分：杀手
- 收获：没有
7号考完的，今天还不出分，是自己也知道教考分离调不出分吗？
给分很好，上调几分
- 课程难度：中等
- 作业多少：中等
- 给分好坏：一般
- 收获大小：没有
- 难度：中等
- 作业：中等
- 给分：一般
- 收获：没有
考完组合数学来评价算法了😭😭😭算法还是比组合数学考的简单啊
算法给分好高啊，寝室大家都是90多，也算是平衡了组合数学70多的分
- 课程难度：中等
- 作业多少：中等
- 给分好坏：一般
- 收获大小：一般
- 难度：中等
- 作业：中等
- 给分：一般
- 收获：一般
今年依旧教考分离，说实话要是只看今年的卷子，PPT上大部分算法你都不用细看，那些看不懂的包不考的，点名概率算法，后面那些模p平方数、因数分解、二次剩余啥的这么多年的考试里没见考过，不如看看概念把前面的选择题正确率保证保证
回忆版题目：（plq另一位同学已经截出来了，可以参考那个评论）
选择10道，一道3分；简答两道，一个10分一个15分；算法设计45分（也是逆天，算法设计能整这么多）
选择题
1、概念题，有关概率算法期望执行时间什么的
——往年第1题都是这种类型的，看看概念就会
2、把概率算法的作业第1题改了改，把y改成了y = 0.5sin(πx)，返回值改成了2k/n，问你最终返回值是多少
3、考察Las Vegas算法的执行时间，期望时间为288，错误概率为0.2，成功时的s(x) = 8，问失败时的执行时间e(x)
——往年题
4、一个一致的、3/5正确的、有偏的MC算法，要求出错概率不超过ε，问至少调用多少次
——往年题
5、袋里球编号各不相同，第一次摸到编号为7的，后面再摸了12次又摸到编号为7的，问球有多少个
——也是往年题，但是这题的答案不太清楚，今年每个选项里的数字都和往年的不一样，不知何意味，我有印象的是12、60和120，还有一个不记得了，但是往年选项里是16、36、64、96
6、异步环的消息复杂度下界
——概念题
7、x是id里最小的，y是id里最大的，问同步环均匀算法的消息复杂度是多少
——往年题，但是偷偷把时间复杂度改成了消息复杂度，答案是不一样的（没想到吧）
8、问哪些环是没有空隙的
——往年题，甚至数都一个没改
9、考察Lamport时间戳，就是这张PPT上的内容
10、同步环的消息复杂度下界
——概念题
简答题
1、已知某个问题没有高效的O(n^2)复杂度的Motor Calor算法，那也不存在期望时间为O(n^2)的Las Vegas算法，判断这个说法是否正确，说明理由
2、构造16个节点的环，使其高度对称，写出所有序等价的片段
——往年题
算法设计题
1、题目很会包装，但本质就是写一个最小顶点覆盖的近似算法，近似算法PPT最后两页有，可以直接抄
2、用Las Vegas算法设计一个求哈密顿回路的算法，给出大致思路及分析，并说明时间复杂度
——往年题
3、在一个无向连通图里设计一个leader选举算法，说明其正确性并分析消息复杂度
能看到往年题占比非常大，你把往年题做会就拿到至少一半分了（算下来该叫这几题叫学长了，十几年的老题目），其次就还是之前说的，那些特别复杂看不懂的算法直接跳就完事了，包不考的
