2026春 2025春 2021春 2020春 课程号:01118601
- 课程难度:中等
- 作业多少:很少
- 给分好坏:一般
- 收获大小:很多
| 选课类别:计划内与自由选修 | 教学类型:理论课 |
| 课程类别:本科计划内课程 | 开课单位:计算机科学与技术系 |
| 课程层次:专业选修 | 学分:3.0 |
算法与理论是计算机科学的核心领域之一。随着大数据时代的来临,传统的算法理论已经不能很好地解决人工智能、物联网、工业制造等领域所遇到的实际问题。本门课程主要介绍基于大数据的新型算法技术,如随机采样、数据降维、数据压缩、分布式计算、流数据计算、聚类、分类、随机优化等,以及相关的理论和数学技巧,如概率计算方法、vc维、通信复杂度、机器学习学习理论等。作为一门理论方向课程,帮助学生掌握解决大数据问题所需的理论和算法工具,为相关领域的工程实践打好基础。
教学水平与风格
丁虎老师本课程的教学风格偏向小班研讨,强调思考与推导。虽然没有教材,助教会整理上课笔记,但听课时做笔记仍然重要。大多数学生认为老师讲解认真,启发性强,授课清晰且有趣,但也有学生认为上课体验欠佳,讲义模糊,板书难以自学。
课程内容
课程内容聚焦于大数据算法,偏重理论与数学证明,涉及大量分析技巧和算法思想。学生普遍感受到课程内容难度较大,但收获丰富。课程中强调对算法的理解与知识的深入探讨。
作业
通常有三次作业,难度较高,需要扎实的数学背景和对算法的深入理解,部分题目被认为“不知从何下手”。在某些年份,这门课没有传统作业,只有小组答辩,要求实现并改进算法,关联性与课程整体内容不强。
考试与评分
考试难度普遍被认为较大,尤其是期中考试,在期末前几天才公布成绩,导致压力增加。期末难度相对降低,主要考察上课讲授内容和算法的记忆。部分学生表示期中期末考试后进行了调分,最终给分较为宽松,但过程不透明,优秀率高。
总体评价
课程具有挑战性,但老师授课效果好,收获丰富。适合已有较强数学和算法基础的学生选修,自学难度大,建议制作详细笔记和充分复习。由于课程内容与考试相关性较高,听课时认真理解有助于考试表现。
- 课程难度:中等
- 作业多少:中等
- 给分好坏:一般
- 收获大小:一般
- 难度:中等
- 作业:中等
- 给分:一般
- 收获:一般
2025春季期中试卷:
1.X~Binomial(n,p),分别使用马尔可夫不等式、切比雪夫不等式和切尔诺夫界求解P(X≥an)的上界,其中p<a<1,并给出p=½ ,a=¾ 时的界限。
2.假设有一个随机算法能够以½ +δ的概率正确判断真假,独立进行N次实验,按少数服从多数表决。若希望错误概率不超过ε,则实验次数N至少为?
3.给定d维点集P={p1~pn},希望找一个k维子空间E做PCA,即minΣ||pi-Π(pi)||^2,其中Π为投影,证明当k=0,1时,该k维子空间E包含点集P的重心。
4.简述k-means++的算法内容,给出时间复杂度和近似比,同时解答为什么此算法选择初始点不直接采用贪心算法而是依照概率。
5.分别以p,q为球心,r为半径画球,定义H=B(p,r)∪B(q,r),t=w(p,q),r=4t/δ,当球H内部的顶点个数占全部顶点的比例小于γ时,我们近似p和q相等,求此γ。
6.给定度量空间的n个点{xi-xn},设Δ=max d(xi,xj),对c>1,考虑Ai=[c^i,c^i+1),ni为落在Ai内的两点间距离个数。证明,存在j,logcΔ-logc2≤j≤logcΔ,使得nj≥(n-1)/logc2。(这几个都是以c为底的对数)
7.无向图G=(V,E),V={A,B,C,D,E,F},E={(A,B),(A,C),(A,E),(B,C),(D,E),(D,F),(E,F)}。回答两个问题:(1)画出图G;(2)在执行Karger算法的第一步时我们收缩边(E,F),画出收缩后的图G',并计算在执行完Karger算法的第三步后,原始图中最小割的存活概率。
8.在d维欧氏空间下,有哈希函h(u)=(<u,Vh>+th)/T下取整,其中Vh~N(0,1),th~[0,T],T为常数。试证明,空间中两个点u和v在哈希函数的映射下碰撞的概率上界与其距离||u-v||2成负相关。也即,距离越大,碰撞概率越小。
已更新期末试卷:
You never actually own a paper, you merely look after it for the next generation.
- 课程难度:困难
- 作业多少:中等
- 给分好坏:一般
- 收获大小:一般
- 难度:困难
- 作业:中等
- 给分:一般
- 收获:一般
老师讲的非常好,但是我学不进去是我的问题。
感觉这课有点太难了吧,是我太笨了吗?
这个课适合nb的人听,可惜我是菜鸡。
- 课程难度:简单
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:简单
- 作业:很少
- 给分:超好
- 收获:很多
这课真的很好,一点都不难,老师讲得好,本着好课一起分享的原则,我建议大家都来选这个课
- 课程难度:困难
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:很少
- 给分:超好
- 收获:很多
辅修人,提前交卷润了。受到某TCS群友影响选了这门课,内容可以查看主页(pksq有)。这门课难度还是比较大,很多地方充斥着一些分析技巧和trick,理解起来需要花一番功夫。但是考试比较简单,期中期末都是默写大赛,且有调分,期末更简单一些,类似于默写xx算法以及一些简单的作业题证明。熟悉讲义和作业就可以轻松做出来。但是辅修人两天三考实在是过于极限,只看了一上午,估计最后要2开头了。
由于叠课+早八的缘故,这学期还是翘了不少课(雾)不过丁老师上课还是非常有趣的,如果能跟上还是很清楚的。相比较而言讲义的更新速度就比较慢了,而且typo较多,前几次的讲义更是直接传承往届的一点不改,希望以后的助教能够一届一届的慢慢完善吧。
- 课程难度:困难
- 作业多少:很少
- 给分好坏:一般
- 收获大小:很多
- 难度:困难
- 作业:很少
- 给分:一般
- 收获:很多
本课程难度较大,但收获也确实很多,请慎选。
丁虎老师在美国做过几年短期助理教授,目前是中科大的特聘教授。
授课风格比较偏向于小班研讨。上课的时候会带着大家思考与推导,而不是机械性的灌输,跟着老师的思路走下来能学到不少。
老师上课是没有教材的,但是有助教整理出来的笔记,老师在课后也会发上课的板书。不过还是建议听课的时候做笔记,不然复习的时候会很痛苦。
去年的整理笔记:http://staff.ustc.edu.cn/~huding/data%20course.html
作业一共有三次,难度比较高,大部分题目都要求良好的数学基础以及对算法思想的理解。
期中考试的难度较大,有60分是上课或者习题课上直接讲过的内容,40分是算法的理解和运用;
期末难度降低了一些(可能是因为期中成绩比较惨烈),全部都是上课讲过的内容。
期中期末成绩分布:
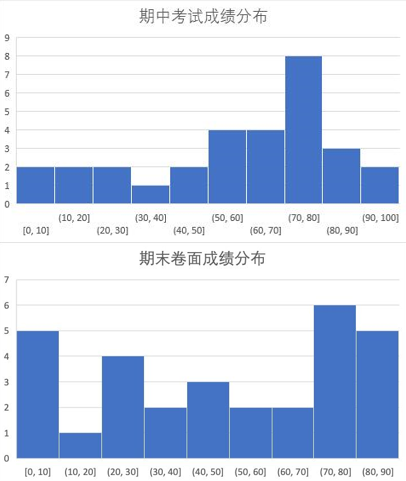
(不是我截漏了,是期末最高分只有90,可能是因为最后一题的fast-JL大家都没背)
黑点主要集中在两方面:
- 如你所见,我上面发的整理笔记是去年的,今年的上课内容和去年有所不同,而助教只整理了一部分笔记。老师的板书也十分意识流。加上没有教材,因此自学是行不通的,上课的时候一定要做笔记。
- 改卷、出分太慢。期中考完快一个月才出分,期末三星期左右出分,又过了两星期才出总评。
主观上,我个人的上课体验是很不错的,可以说是我大学期间一字一句认真听完的唯一一门课。
给分上还算不错,期中期末改卷都放了大洪水,最后总评也调了分。本人期中期末都只有八十几分,最后调到了九十几。
- 课程难度:简单
- 作业多少:很少
- 给分好坏:一般
- 收获大小:一般
- 难度:简单
- 作业:很少
- 给分:一般
- 收获:一般
.这个笔太不好用了.
- 课程难度:中等
- 作业多少:很少
- 给分好坏:一般
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:一般
- 收获:很多
大三所有课里最值得上课听的,可能有没有对应教材的原因,但是老师讲得也很好。讲的东西启发性蛮大的。课不怎么文科,和webInfo这种有点差别。考试内容基本都在老师笔记里有,复习基本把笔记都过一遍 不用看什么题。 比较烦的点:作业奇难无比,不是巩固作用的,以启发为主,虽然最后一般也没被启发;发课堂笔记和出分都很能拖。
- 课程难度:困难
- 作业多少:很少
- 给分好坏:一般
- 收获大小:没有
- 难度:困难
- 作业:很少
- 给分:一般
- 收获:没有
丁虎老师是从密歇根州立大学回来的老师,这门课也是2020年疫情期间第一次开设。
(注:17级计算机专业的专业选修课有调整,增加了大数据算法这门课以及张兰老师的数据隐私课程。即使这样,cs的专业选修课依然乏善可陈)
丁老师上课会用板书讲各种大数据算法,偏理论证明,牵扯到很多数学上的内容。这个时候数理基础不扎实的问题就暴露无遗,而且上课不认真的话,课下看板书也看不懂。课下的话助教会总结丁老师上课讲的内容,整理成notes的形式发给大家以供复习参考。这点体验是相当好的。
这门课(2020春)没有作业,只有最后的一个小组答辩(可以单人答辩,也可以双人答辩):从丁老师给的5个主题中挑1个进行深入研究,然后实现算法并改进,最后总结成标准的论文格式。从这一点上看,其实和课程整体内容的关联性并不强。
- 课程难度:困难
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:很少
- 给分:超好
- 收获:很多
一分扣在讲义有些地方讲得比较模糊,理解内容还是要靠录像学。
考试前的习题课一定要听,会强调一些“要掌握的”内容,包括平时提到某内容考试范围只占哪一部分,基本上也是会考。个人感觉期中考难一点,期末考简单一点,主要是期末考除了最后一题之外都强调过,最后一题基本上是作业题的简化,对这些内容要是熟悉的话基本上就是默写了。
- 课程难度:困难
- 作业多少:中等
- 给分好坏:一般
- 收获大小:很多
- 难度:困难
- 作业:中等
- 给分:一般
- 收获:很多
内容挺难的,不过丁老师是完全板书,讲得很认真,听课的话跟上还是没问题,而且挺有意思的。但是作业和考试、给分太一言难尽了,只有三次作业,每次几道题,难度不小,有一部分甚至是无从下手的那种,甚至还有老师随口一说的那种题,什么求矩形的VC-Dim(答案是7,反正我是做不出来……);考试成绩分布有同学贴上去了,期中考试的成绩直到期末前几天才出,最后肯定是调分了,但具体怎么折腾的我们都不大清楚,但是如果新同学估摸着自己考试大概在50%左右又重视成绩就还是别上了……
总结的话就是听课体验很好,丁老师讲得也很清楚,内容也很有意思,但是如果选课了就一定要好好学多复习,不然分数会很难看
- 课程难度:困难
- 作业多少:中等
- 给分好坏:一般
- 收获大小:一般
- 难度:困难
- 作业:中等
- 给分:一般
- 收获:一般
老师讲义和改卷速度奇慢,上课体验极差。个人感觉老师对教学不上心,也没有正规教材,自学都学得很痛苦。也不知道是助教鸽子还是老师鸽子。
开学时候本来有快100个人,期末只剩下30个人了。
有期中期末,本来各占40%,但是因为两次考试都有很多人不及格,也不知道最后怎么瞎调的。优秀率应该是给满了。但反正也就30个人…