2023.10.4 更新：

睡前刷知乎发现，上海交大的傅育熙老师牵头写了一本《计算复杂性理论》教材（出版社链接），不知道写得怎么样，感兴趣的同学可以关注一下。

附上海交大“计算复杂性理论”课程主页：https://basics.sjtu.edu.cn/~yuxi/teaching/complexity/

2023年春季学期我正式选修了这门课。今年是这门课开设的第3年，或许是因为前两次开课产生了一些好评，今年的选课人数由前两年的50人以内增加到86人（教学秘书安排的教室只有78个座位），一开始大家只能从隔壁教室搬座椅（但由于开设了线上直播，之后来上课的人也就变少了）。本学期的授课时间是1-10周，每周一下午连上4节 (6,7,8,9)，其中第9周五一放假，第10周习题课，因此实际只上了32个学时，勉强上完了时间复杂性，只简单提了一下空间复杂性。这学期上下来，能明显感受到黄老师上得更熟练了，而一如既往不变的是黄老师对于课程准备的用心程度：例如，前面几周每次上完课，都会在群里面发布匿名投票，认真倾听同学们的反馈；整个学期中及时在课程群里回答大家的问题（课程群开放匿名，且氛围异常好，同学们都很认真地交流和讨论问题）。

当然，个人认为也有一些美中不足的地方。正如我在下文中写的那样，由于黄老师当年是被硬拉来上的这门课，本身并不是做计算复杂性相关方向的，因此在课程中黄老师经常会用自己熟悉的领域来举例子，但有些时候我认为并不恰当（经常举完例子感觉更懵了）；另外，这门课留给计算复杂性部分的课时较少，这一部分可能会与大家的科研更为贴近。

这学期5月15日考完试，5月18日就出分了，效率很高。出分后，黄老师在课程群里进行了一些总结并对这门课后续可能的调整做了展望，经过黄老师同意分享到这里（因为黄老师不希望后面选课的同学误以为这是一门水课）：

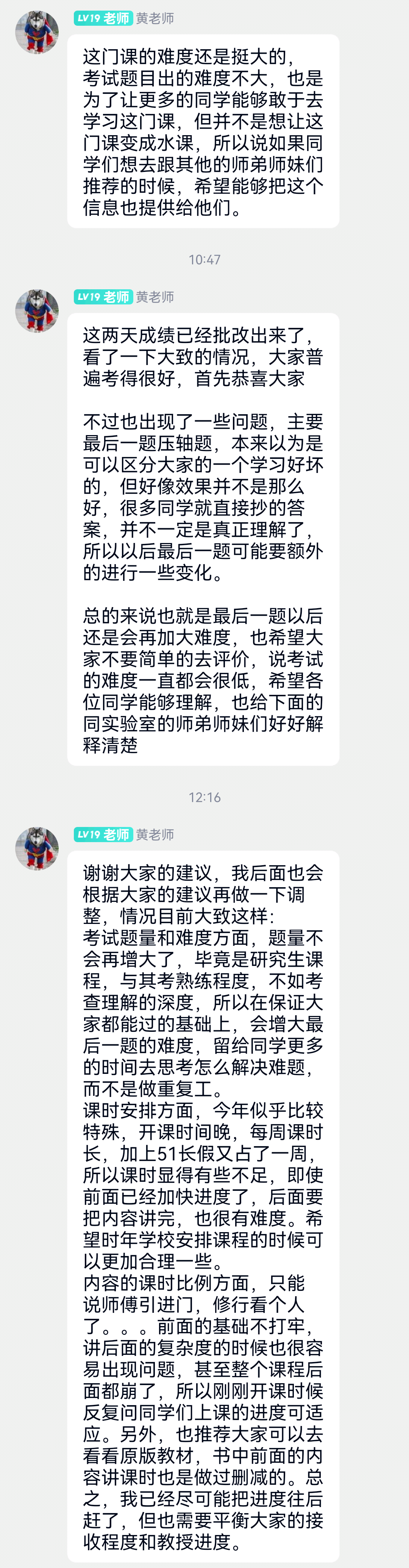
2023年春季学期期末考试题：

1. 下面的逻辑表达式是可满足的吗？为什么？

\((x\vee y)\wedge(\bar{x}\vee y)\wedge(x \vee \bar{y})\)

2. 下列语言中，哪些是可判定 (decidable) 的？哪些是不可判定 (undecidable) 但图灵可识别 (Turing-recognizable) 的？哪些不是图灵可识别的？只需给出结论。

\(A_{DFA}, EQ_{DFA}, E_{DFA}, ALL_{DFA}, A_{CFG}, EQ_{CFG}, E_{CFG}, A_{TM}, EQ_{TM}, E_{TM}\)

注：上述语言中，\(A_{TM}, EQ_{TM}\)不是补图灵可识别 (co-Turing-recognizable) 的，其他语言都是补图灵可识别的。

3. 画出识别下述语言的DFA状态图，字母表为\(\{a,b\}\)。

\(\{w \mid w是恰好不含2个a的任意串\}\)

4. 如图所示：

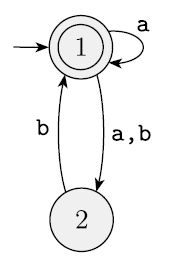
(1) 将上图的 NFA 转换为与其等价的 DFA；

(2) 将 (1) 中的 DFA 转为正则表达式。

5. 给出识别下述语言的下推自动机 (PDA) 的非形式化描述。

\(\{a^ib^jc^k\mid i\geq1, j,k\geq0且(i=j或i=k)\}\)

6. 试证明\(E_{TM}=\{\langle M\rangle\mid M是一个图灵机,且L(M)=\varnothing\}\)是不可判定 (undecidable) 的。

(以下内容写于2021年春季学期结束后)

说明：我没有选修这门课，但前前后后旁听了一半多的课时，所以下面的评价主要针对课程本身，关于考试和给分的具体情况请其他同学补充。

这门课是2020研究生新版培养方案中新开设的，计算机软件与理论专业的基础课，40课时，2学分。这学期的上课时间是15-18周，每周两次课，每次上一个上午，实际授课28课时。

（补充说明一下，为什么到期末才开课呢？据黄老师说，由于是第一次开课，且课程难度较大，学院大部分老师不愿意上，上学期期末教学秘书才找到黄老师，最后黄老师不得已接下了这门课，所以这学期前面一大半时间都在准备。）

这门课使用的教材是Sipser 的 Introduction to the Theory of Computation, Third Edition，在课程主页上有电子版（链接）。对应的中译本是《计算理论导引》（原书第3版）。

课程内容主要包括三个部分：自动机理论（计算的模型）、可计算性理论（哪些问题可计算？哪些问题不可计算？）、计算复杂性理论（哪些问题是难的？哪些问题是容易的？）。

• 第1章 绪论 (对应教材第0章)
• 第2章 Automata and Languages
  • 2.1 Regular Languages (对应教材第1章)
  • 2.2 Context-free Languages (对应教材第2章)
• 第3章 Computability Theory
  • 3.1 The Church-Turing Thesis (对应教材第3章)
  • 3.2 Decidability (对应教材第4章)
  • 3.3 Reducibility (对应教材第5章)
• 第4章 Complexity Theory
  • 4.1 Time Complexity (对应教材第7章)
  • 4.2 Space Complexity (对应教材第8章，2023年春季学期只用20分钟时间把主线过了一遍，没有时间展开讲)

实际上课程中的很多内容大家在其他课程中多少接触过一些，但这门课是对这些知识的一个系统的讲解，每一个定理都会经过严格地证明。

黄老师在第一次课就说，这是一门数学课，难度是比较大的，经常提醒大家要及时预习和复习，保证充足睡眠。虽然是第一次开课，但看得出来，黄老师是在很用心地对待这门课，课件制作得很精良（可以称得上是赏心悦目），并且每讲完一处比较难的地方会停下来问大家听懂了没有，大部分同学都听懂了才会继续讲，否则会停下来和大家讨论，或再讲一遍。这也是我给10分的原因。

课程的考核方式是半开卷（可带一张手写A4纸）。据黄老师第一节课所说，80%的题目与作业相关，剩下的20%是压轴题，会考课程中所讲到的一个证明。

由于是第一次开课，难免有一些不足。首先就是上课时间，这门课期末才开课，大部分同学都在考试，所以压力是比较大的（不过从明年开始就会和其他课程一样从学期开始就上课）。另外，可以看得出黄老师在尽力把内容讲明白，但因为是第一次上课，很多地方显得不太熟练，偶尔也会有一些小错误。但我相信后面会上得越来越好！

最后还想多说几句，我们为什么要学习计算理论？这里引用南京大学尹一通老师在豆瓣上给《计算理论导引》所写的书评（链接）中的一段话，与大家共勉：

然而，尽管我对这本书和这门学问都很推崇，我对于学习计算理论的必要性却并不坚定。我自己喜欢这些，可我该如何向别人解释学习它是必要的？

Sipser在前言中也试图说明这个问题:"After all, isn't theory arcane, boring, and worst of all, irrelevant?"
他很认真的试图从几个方面说服学生，计算理论是“有用”的，但我总觉得这些说服很徒劳：书中的三个部分，对于搞研究的人来说，前两个领域已经或走到头了或不再是主流研究趣味了，只有复杂度尚活跃，但也只是个理论方向之一；而对于那些有志于业界工作的学生，后两个部分几乎永远不会在工作中用到，而只有第一部分的自动机，可能会用到一点点正则表达式。

看来，从“有用”这个方向去为计算理论辩护，难免会遭遇尴尬和勉强。

我能想到的理由就只剩两个：
（一）这些是计算机科学的根本，没有它们计算机科学不能算作是个正经学问，因此，一个自称计算机科学专业的人，应当知道这些。
（二）这些是美好的，值得在短暂的人生中去经历去见识。

我觉得这已是足够的理由了。

感谢黄文超老师，让我在科大计算机学院听到这样一门优质的课程。推荐大家明年来选！

我没上黄老师的这门课，但我还是想点评（瞎说）一下。

我觉得黄老师的PPT写得很好，把书上的重点写出来了，为同学们省下了大量的时间。

如果课上听不懂或者实在没办法翘了课，也可以听听Sisper老爷子的网课，他讲的非常好（毕竟书也是他写的～）。

另外，我感觉这种课挺难、挺硬的，不是那种可以突击的课。所以选课时要慎重，比如可以想想自己是否有时间或者是否对算法/形式化方法/计算理论感兴趣。

(暴论一句：相比什么大物实验、量子物理、数理方程，这才是属于CS学生的数理基础！）

我的笔记：形式语言与计算复杂性笔记.pdf

计算理论基础不是难课：

据我所知这门课在 FDU、ZJU 和 NJU 都是本科必修课程。

相比本科的离散数学（数理逻辑），计算机系学生能在计算理论课程中找到更多熟悉的讨论对象：

• 自动机理论和编译原理（虽然你未必要写 parser，写 parser 也未必会使用 CFL，处理 CFL 也未必需要 parser generator）；
• 图灵机和 λ calculus：都是某种对计算的抽象，都有明确的操作语义；
• 复杂度理论：嘛，毕竟本科数据结构和算法课就已经接触过无数的例子了。

而且计算理论中更多的证明都是「proof by construction」，很多都可以直接被翻译成对应的程序。因此相比妮可本科灌输的几门数学课，计算理论确实是更让人有亲切感，也更配被称为「计算机科学」的「理论」的一门课。我想这就足够成为学习的理由了（姑且不谈邱奇-图灵论题的哲学内涵这种神棍话题）。

讲课：

美中不足的地方。老师上课会有些不严谨的地方。直观理解是没什么问题，但如果当成数学课还是应当更追求准确性（这门课教材基本上是严谨的）。

因此在课程中黄老师经常会用自己熟悉的领域来举例子，但有些时候我认为并不恰当（经常举完例子感觉更懵了）

以 2025 年 The Church-Turing Thesis 一章授课为例。有些例子我很喜欢，提供了很形象的直观，比如图灵机/configuration和程序/进程的类比。然而这章在讲 multitape Turing machine 时就有两处很明显的问题：

• multitape Turing machine \iff Turing machind。声称为每个纸带初始提供足够长的间距即可是错误的。这个足够长实践上无法达到，因为纸带使用的长度可能和输入长度呈多项式/…等函数关系。而且这里的正确解答实际相当简单，只需要在到达边界时整体移动后面纸带一格即可（见教材）；
• 声称 writing a tape symbol with a dot above 是每个位置存打包的结构体。这个例子不准确，这里是对 Symbol 的扩充，当然也可以看成结构体，但是关键在于它作为 record (product) type 新增的 field (bool) 是有限的，这样新的类型的元素个数仍然有限。

补充：可能期末考试太简单导致老师说以后最后一题要加大难度。可能由于平时作业错了一些导致最后期末总评88，不过也够用了

===================================================================================================

老师：认真负责，有水平，PPT美观高信息密度，讲课内容丰富

助教：存在感不强，本职工作完成得很好

作业：不多，难度中等偏上，由于是外国教科书上的所以实在不会做也不担心找不到答案

考试：半开卷，难度比作业低

考试+A4

扫描文稿(1).pdf

没有上这门课，对计算理论感兴趣，看了黄老师的PPT感觉很好。

希望这门课下放到本科

平时上课难度和考试难度gap太大，所以一开始发现自己听不懂也别急着退课（笑

形式语言A4.pdf

课程属于数学类，需要点想象力，逻辑能力

作业是不难的，考试比作业还简单

课程内容：不多

课程体验：放在周一下午6789节很容易😪

课程难度：中规中矩，有一定前序课程的基础不难上手

作业：都是课后题，答案见Github： https://github.com/Alpha-Girl/sipser-computation-3rd-solutions

考试：最无语的就是只能

手写

A4纸，浪费时间

给分：很好，4.3飘过

总体不用花很多时间，还可以学到东西，推荐

老师很负责，讲的东西很细，每节课都会根据反馈调整讲课速度；课件做的很精细很有调理。

作业布置的略多，但是都不算难，跟课程相关性很高，很适合拿来复习；

考试难度不高，可以无压力去认真学习课程内容；

老师说了好多次的类似于“选课的人这么多，是我更认真备课的理由”，加上知识点确实对于计科来说是很有价值的，综合讲是很值得选的一门课

没办法，这门课是理论方向的基础课。

老师：上课很负责，每节课课后都询问上课情况，同学能否跟上进度，不点名。（真的很负责一个老师！）

考试：半开卷，一张A4纸，卷子比作业简单，作业做了就会写。（才一个小时就有人交卷，大家也知道简单了）

上课就八周，需要点想象力，不然后期上课不知道在讲神恶魔

复习两天还是浪费时间了，课一次没去最后98，但是多少分和60都没有任何区别。至少有一天花在这课上是浪费了，还有7次作业有点多，抄抄都要半小时。

回忆卷：1.PCP原题 2.TM状态怎么变 3.泵引理 4.写个DFA 5.NFA转DFA 6.SAT转3SAT和是否可满足 7.两种方法证A_CFG可判定

73分飘过，不过能及格就ok

优点：不用写代码，不用pre,仅7次作业，仅考试，考试很多作业原题，允许带一张a4纸。

缺点：有签到，课程确实有些抽象，7次作业也有点多。

这门课程是2023级计算机学院计算机软件与理论方向学硕培养方案里专业选修课四选二的课程之一，但是2023学年只开设了形式语言、高级软件工程、高级操作系统三门课（也有可能我记错了），这意味对于软件与理论方向的学硕只有三选二的可能，那似乎看起来形式语言是最友好的一门课，几个因素：不点名（实际今年点名占了10%的总评），给分友好（今年给分有一半人以上优秀，且只有零星几个不及格），使其是个人认为的软件与理论方向的必选课（不会有人同时选了必点名的高软和给分屎的高操吧）。

PPT的内容是计算理论导引这本书前几章的一个子集，因为我不太看的明白PPT，看书的中文版会有更好的效果。这门课是计算机学科中比较数学的一门课程，相对来说难度比较大。上课一共四次点名，占10%。

作业是课后习题，有祖传答案，一共七次作业，每次写都需要看一天，工作量在研究生课程中算比较大的。

考试难度尚可，主要考作业内容和课本的证明，如果理解不能就比较考验A4纸的缩印能力，当然如果能当人肉SSD也能拿到不错的成绩。

给分友好，非常适合计算机学院下学期学分不够或是计算机软件与理论方向的同学修读。

我个人认为这是科大计算机学院开设的最有价值的课（之一），不适合完全想划水的，课程有难度，但其实老师讲课难度相比原教材难度已经降低很多了

虽说是手写一页纸开卷，但我感觉这张纸其实并用不上，写这张纸本身就是一次很好的复习机会

考试题目绝大多数都是作业题类似的，甚至还有原题。个别题作业没有过，需要现场想想，不过难度也不是很大。

anyway，会签到，占比好像有10%，会影响分数（亲身体验）

黄老师应该是我来科大以后，遇到的对课程最认真负责的老师了。

我觉得黄老师讲课讲得很好。我上课的时候注意力不集中，容易跟不上，但下来看了课程的视频回放之后，其实发现黄老师讲得很清晰，很多概念和证明一下就理解了。

算是合格的研究生课程，7次小作业但是都有答案，压力不会很大，上课是没有听过的，期末学两天把A4纸疯狂抄作业题，4.3拿下

期末跟作业题很像，搞懂了问题就不大，最后一个证明题记得是A_CFG可判定的证明吧，要求写出两种，其他的作业题往年题都覆盖到了