2021春 课程号:00718601
- 课程难度:困难
- 作业多少:很少
- 给分好坏:杀手
- 收获大小:一般
| 选课类别:计划内与自由选修 | 教学类型:理论课 |
| 课程类别:本科计划内课程 | 开课单位:地球和空间科学学院 |
| 课程层次:专业核心 | 学分:3.0 |
教学水平
刘睿老师有较强的科研能力,但在表达上有不足,导致部分同学上课听不太懂。课程内容偏重数学结构背后的物理本质,采用D.D. Schnack的教材,每一堂课是一个独立的话题。部分同学反映,老师上课时语气变化不大,板书主要是公式推导,缺乏变量的解释和结论的引出,容易让人云里雾里。
课程内容
课程内容涵盖了磁流体力学的多个方面,包括矢量、张量分析,基本方程与基本性质,平衡态及其稳定性,波动和激波,不稳定性、磁场重联以及其他非理想MHD的重要话题。刘老师采用了Schnack的讲座式风格,每次课一个话题,逻辑衔接,但可能对学生来说不太习惯。
作业
作业布置较少且与期末考试关联不大,多靠学生自觉。部分同学建议课程作业需要更有针对性和引发思考,以更好地帮助理解和复习。
考试
考试为两个半小时,共七道选择和三道大题,总分50分,开卷。考试题目与作业关系不大,需要长期积累和理解。考试难度较高,期末考试及格的同学较少,平均分偏低。
给分
总成绩由平时分(作业分,占50%)和期末考试分(占50%)构成。给分严格,没有调分,优秀率和挂科率较低,比较公平但严格,部分同学对优秀率较低表示震惊。
总结
刘睿老师的《磁流体力学》课程内容丰富且深入,但由于课程讲解方式及准备时间较短,使得部分同学难以适应和听懂。平时分与期末分各占一半,期末考试难度较大,给分严格。该课程适合对磁流体力学有较强兴趣且在自学能力上有较高要求的同学。
- 课程难度:中等
- 作业多少:很少
- 给分好坏:一般
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:一般
- 收获:很多
今年2月初临时接到任务教这门课一学期,备课很仓促;也是第一次给本科生上课,确实没有经验。课程讲了一小半才选定D.D. Schnack的“Lectures in Magnetohydrodynamics”,推荐给大家重点参考,这是Springer出版社的书,校内可以直接下载pdf,但似乎没有几个同学有闲情读这本书。上课的时候也只有坐在前面的几个同学听讲和记笔记;大部分人挤在后排,无数次板书后回头看见他们谈笑生风。期末考试只有四个人及格(30分以上,总分50),算是意料之中吧。总评成绩分布是难看了点,但”也许,这就是人生吧“,一分耕耘一分收获。
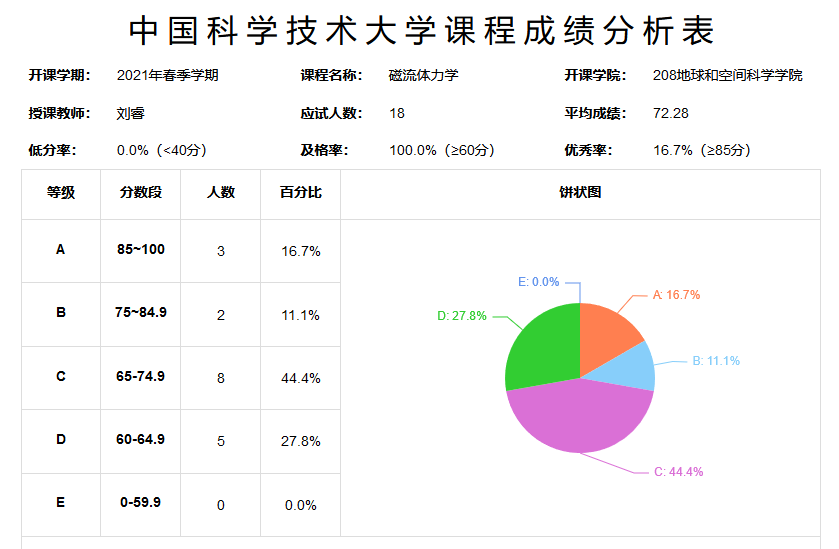
- 课程难度:中等
- 作业多少:很少
- 给分好坏:杀手
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:杀手
- 收获:很多
前言(临时)
这篇评课主要完成于去年结课后,但由于内容没有校订一直拖到了现在(咕咕咕)。一转眼19级也要开始学MHD了,于是赶紧赶工把这篇评课发了出来。21春的 MHD 由于汪老师有事出差所以是刘老师临时代上的。22春应该是变回汪老师上。本人由于曾在20春旁听过汪老师的 MHD,所以也对汪老师的课程稍有了解。本文主要按刘老师的思路介绍 MHD,19级的学弟学妹可以当做看待 MHD 的另一个视角,作为汪老师课程的补充。
风格概述
MHD 是一套简洁而优美的理论,这门课也是空物本科期间最后一门物理味十足的课了。
两位老师都注重公式推导,但在这之外两位老师的侧重点有所不同。汪老师更倾向于介绍各种模型的求解和应用场景;刘老师更偏好解释这个理论中数学结构背后的物理本质。汪老师的课主要按照 Eric Priest 的 MHD of the Sun 的前几章(MHD基础)来进行的(Priest 的书本身就是介绍各种 MHD 的模型在解释太阳现象的应用)。而刘老师则采用了 D.D. Schnack 的 Lectures in Magnetohydrodynamics 的思路。(Schnack可以看作是 Freidberg 的 Ideal MHD 的精要,主要介绍 MHD 的物理原理)。此外,汪老师的课与 Priest 的书一样是传统的章节型进行的;而刘老师的课则是采用了 Schnack 的讲座式,每一次课是一个话题(话题之间的顺序仍是按物理的逻辑衔接的)。由于科大此前的课程很少有按讲座的顺序组织的,所以可能对同学们来说不太习惯。
课程内容概述
如前所述,这门课由一系列话题构成,这里将这些话题依顺序合并为几个主题。试着加入了一些评论帮助大家理解,希望排版没事(
【数学基础】
1. 矢量、张量分析,曲线坐标系,格林公式(高斯/斯托克斯公式)
【基本方程与基本性质】
我们需要从基本的物理原理出发,在特定的适用条件下得到 MHD 描述体系演化的方程组(2)。和流体力学一样,我们自然也会考虑其相似律(3)。而 MHD 描述的对象中,至关重要的一个便是磁场如何演化(4)。进一步的,磁场演化规律的背后是 MHD深刻的拓扑结构(5)。至此,我们在一般的情形下初窥了 MHD 的基本特点。
2. MHD 的适用尺度与基本假设,基本方程的导出与守恒形式,以及广义 Ohm 定律各项的解释
3. 无量纲化MHD 方程组,Reynolds 数,Lundquist 数
4. 磁力线,磁扩散(磁湮灭),理想 MHD 的磁冻结
5. 理想 MHD 磁螺度的拓扑不变性(以及相对磁螺度的规范不变性);非理想 MHD 电阻对磁螺度的耗散
【静力学(平衡态)】
接下来,我们在具体的情形下进一步了解 MHD 的行为。从最简单的情形——所有演化项统统为 0 的平衡态开始。我们想知道,什么样的磁场能够处于平衡态。对于平衡态,位力定理自然是我们的老朋友了(6)。而具体到 MHD 中,需要考虑好如何平衡 Lorentz 力。它可以与热压平衡(7),也即热等离子体所关心的箍缩;它也可以直接为零(8),这样的磁场称为无力场。接着,因为平衡态的体系能量处于极小值,我们自然会想从能量的角度考察磁场(9)。平衡态不仅处理起来友好,而且适用也广泛,许多演化缓慢(静态)的结构可以用准平衡态来分析。
6. 位力定理;无外加电流时无法实现平衡态
7. 柱坐标下的各种箍缩;普适的Grad-Shafranov 方程
8. 无力场(势场,线性无力场,非线性无力场)
9. 磁能的最低态——线性无力场与势场;磁扩散对磁自由能的耗散
【平衡态的稳定性】
由于平衡态很多时候不能严格成立,我们自然地还想关心对平衡态的微小偏离意味着什么,也即考虑平衡的稳定性(10-13)。这里进行了一些偏formalism的讨论,使用到的方法会贯穿后面的内容。总的来说,MHD 方程中的各项有的使系统倾向于稳定,有的则不稳定。在它们的总影响下所得到的角频率的虚实,将决定系统面对扰动是发展出不断增强的不稳定性(23-27),还是得到稳定解的波动(16-20)。
10. 微扰矢量(函数)与力算符(泛函);动力学方程本征值问题的 Dirac 符号表述
11. 理想 MHD 力算符的自伴性及其证明
12. 分析理想 MHD 平衡态稳定性的方法:本征值问题
13. 分析理想 MHD 平衡态稳定性的方法:能量原理
【补充(杂谈)】
注:这部分是课程中间插入的一部分内容,作为对早期内容的补充。
14. MHD 磁通量管与流体力学的涡管的类比
15. 从最小作用量原理推导 MHD 的动力学方程
【波动】
回到主线,开始分析一些动态的演化。首先考虑偏离平衡态后的稳定解:波动。对于波动,最核心的问题是得到它的色散关系(这将描述它如何传播)。或者说,与其求解复杂的偏微分方程组,不如在小尺度波的条件下将其线性化并 Fourier 分解,成为方便求解的代数方程组。只有所允许存在的波动解能使这个代数方程组成立(与由 MHD 导出的原 PDE 相容)。而使这个方程组有非平凡解的条件正是色散关系,对应的解则为允许存在的波模(16)。对于 MHD,这样的色散关系有三个,对应三支波的模式(17)。而这样的波自然也携带了能量和动量(18)。事实上,我们也可以对 MHD 进行拓展。先前导出 MHD 时我们忽略了一些具有物理意义的项,现在我们将其中的一些重新引入,那么原本简并的波模就会分裂并耦合出新的解,得到哨声波等等离子体波(19)。最后,回到一般的 MHD 波,作为色散介质中传播的波动,我们自然也关心它们的相速度和群速度(20)。
16. 无穷边界的 MHD 方程组;色散关系;MHD波的模式
17. Alfven 波、快/慢磁声波的性质与物理分析
18. 波的能量与动量;再谈色散关系
19. 广义 Ohm 定律对 MHD 波模的修正(Hall 项和惯性项的修正);有限空间中 MHD 波的修正(无法线性化,回到本征值问题)
20. 从第一性原理(最小作用量原理)考察能量的传播速度,能量子的连续性方程
【激波】
在允许介导波动的介质中,如果存在对应的扰动,则可以引发相应的波动。而其中有一类极端的情况:扰动源移动的速度大于波动传播的速度。这种情况下将出现间断面,两侧的一些物理量发生突变。
注:可控核聚变不怎么涉及激波,因此 Schnack 的书并不讨论激波。但空间物理中激波却是十分重要的(例如,地球相对于高速太阳风而言就是一个高速移动的扰动源,速度超过太阳风中传播的 MHD 波),所以在 Schnack 之外补充了这部分内容。
21. 守恒形式的间断表述;质量通量的方程与解的模式:间断面与激波
22. 激波模式的物理分析;共面定理
【不稳定性】
对于角频率为虚的系统,即使是一个小扰动也将不断增强最终颠覆整个系统(23)。例如,上重下轻的流体的平衡是不稳定的,任意的一个微小的上下交换就会触发正反馈(24)。又如,存在切向速度间断的流场也是不稳定的(25)。我们将考虑这些流体力学中经典的不稳定性在磁场的存在下有何表现(24-25)。此外,前面平衡态讨论的各种箍缩中同样存在不稳定性,有的箍缩总是稳定的,但有的箍缩只在一些条件下稳定,此时只能允许存在特定的波模(26)。最后,我们将考虑磁场如何影响旋转的天体(27)。
23. 本征值问题和能量原理对不稳定性的一般分析
24. 重力交换不稳定性(Rayleigh-Taylor 不稳定性);边界层理论
25. K-H 不稳定性与力算符自伴性的破坏
26. 用能量原理分析各种箍缩中的不稳定性模式
27. 旋转天体的不稳定性
【磁场重联】
理想 MHD 确实赏心悦目,但是有代价的——舍弃了一些项的同时,我们也将无法解释一些关键的物理过程。我们现在尝试恢复其中一个重要的项:广义 Ohm 定律的电阻项。这一耗散项的引入改变了磁场的演化本质(现在允许磁场的连接发生改变),这一项也改变了方程的本质结构,使原先的方法失效,问题变得困难起来。由于实际问题中的耗散往往在一些局部才比较强烈,我们试图将这一耗散过程局限在一个小区域而保留其他空间仍为理想 MHD,以在一个简单的模型下了解有电阻 MHD 的行为(28)。Sweet 和 Parker 最先给出了一个稳定的模型(29),但可惜这样的重联重联率太低,无法解释实际观测到的剧烈而快速的过程。人们转而考虑由不断增强的不稳定性引发的重联(30),但很不幸,它的重联率仍不够。时至今日,磁重联的研究仍在继续。
28. 磁耗散改变拓扑结构;力算符失去自伴性;局部电流片的模型
29. Sweet-Parker 重联(一对相向的定常流挤压磁场发生重联)
30. 撕裂模不稳定性(耗散把磁场“撕”开了)
31. 重联速率的评估
【其他非理想 MHD 重要话题】
我们之前考虑了 MHD 的磁场的种种演化。演化的模式与所处的状态有关,随着演化的进行,其遵循的模式也在变化。那么一个问题是,时间变得足够长后会发生什么?总的来说,耗散导致磁场朝着磁能和螺度降低的方向演化(比如线性无力场、势场)。有趣的是,不管初态如何,演化的终态都惊人地相似。这是耗散MHD 的另一个重要的话题:弛豫(自组织)(32)。
32. 弛豫过程:耗散的终态;能量的耗散 vs 螺度的耗散
大尺度的天体(如恒星、星系)如何形成它的磁场?虽然 MHD 有望给出解释,但Cowling 等人曾指出在诸多情形下磁流体发电机将不可能维持。好在此定理并未否决磁流体发电机的所有可能,湍流的引入给情况带来了转机(33)。
33. 磁流体发电机:Cowling's Anti-dynamo Theorem;湍流与 Parker's Turbulent Dynamo
有趣的话题还有很多,但课程差不多到此结束了,其余的话题感兴趣的学弟学妹们可以自行从 Schnack、Freidberg 等书中阅读。
除了静力学(平衡态)到动力学(波动、不稳定性、磁重联等)的顺序外,本课程还有一条贯穿始终的暗线,即理想 MHD 所具有的良好性质与非理想 MHD 对其的破坏。
理想 MHD 对于磁场而言意味着磁力线的拓扑不改变(一个物理上直观的体现是磁冻结),而另一方面在问题的求解上使力算符具有自伴性。自伴性使得理想 MHD 本征值问题的解空间完备,从而任意的微扰可以用本征矢展开,这赋予了用本征值方法来研究理想 MHD 波动/不稳定性的合法性。而由于微扰引起的效应可以用这组本征矢完备地描述,问题就归结于研究体系具有怎样的本征态矢。只需找到一个不稳定的本征态,就能判定系统是不稳定的,这使得我们能利用能量原理去试探从而更方便地分析其不稳定性。然而,自伴性这一宝贵的品质很容易被破坏,在引入非理想 MHD 的额外的项时,甚至在理想 MHD 中存在无法消去的背景速度场时,都会破坏自伴性从而使本征值方法和能量原理失效,给求解带来困难。而回到物理上,非理想的 MHD 后果是,电阻的磁扩散破坏了磁冻结,磁力线被允许滑动,磁力线的连接发生改变。磁重联、弛豫、磁流体发电机等话题也因此而起。
附一张期末复习课上老师总结的框架,感觉比我写的清楚易懂得多(捂脸):
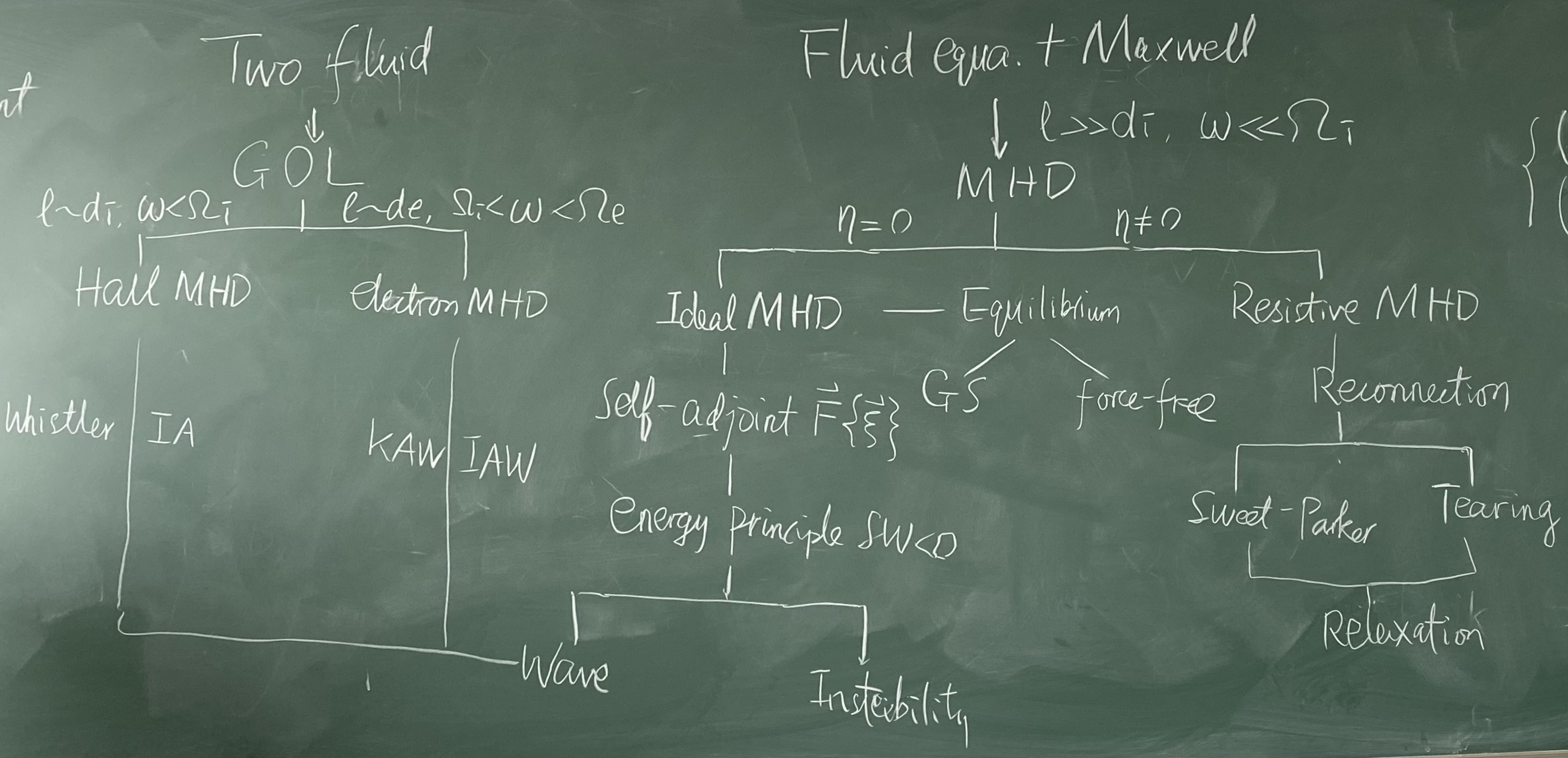
先发到这吧,凭印象校订太麻烦了(当时的笔记落在学校了),等返校后再看看前面有没有要修改的。对课程的评价也下次一并更新。
- 课程难度:困难
- 作业多少:很少
- 给分好坏:杀手
- 收获大小:一般
- 难度:困难
- 作业:很少
- 给分:杀手
- 收获:一般
第一次评课给了刘睿老师。
关于讲课:刘老师很厉害,科研很强,智商也很高,可能高智商人群都不屑于表达低级的东西,导致上课基本听不懂,看老师尬讲,老师沉浸在自己的世界中,所以我感觉老师表达能力不太行,反正我无法领会老师讲述MHD的真谛。这门课老师没有给定教材,但给了很多参考书和以前教授这门课老师的讲义,都是全英文,老师一直板书,但板书只有公式推导,没有变量的含义,导致一直云里雾里。
关于考试:两个半小时,七道选择,三道大题,卷面分五十分,开卷(开卷也找不到,老师原话),一直在找,一直在写,和布置的作业的关系不大。
以上的优缺点都可以接受。
重点:
关于给分:应该是一分没调,五十分平时分(作业分,没有到课率)加上卷面分,目测19个人1~2个优秀,有没有人挂科尚未发现,差不多是这个比例,尽管调不调分都是老师的主观意愿,但是5~10%的优秀率还是让我十分震惊。
以上。
- 课程难度:困难
- 作业多少:中等
- 给分好坏:杀手
- 收获大小:一般
- 难度:困难
- 作业:中等
- 给分:杀手
- 收获:一般
时隔一年,在这一年里我听到了不同老师关于 MHD 的讲解和应用,当我想起一年前刘老师的课程,我会发现其实刘老师讲得更加深入,当然了详细内容确实大部分是记不住的,需要自己把框架和物理图像搞明白(可惜当时我忽略了对本课程的深入理解啊,因此也不难理解考试结果不如人意——当然其实老师布置的作业也不是特别的引发同学们思考,感觉还是靠自觉多一点)。
对于上课,确实承认刘老师的课堂氛围不是那么好(相比以前的一些理论课),也能理解老师是第一次带本科生课程。
也许,这就是人生吧。