2026春 2025春 2024春 2023春 2022春 课程号:MATH5008P01
- 课程难度:中等
- 作业多少:中等
- 给分好坏:一般
- 收获大小:很多
| 选课类别:基础 | 教学类型:理论课 |
| 课程类别:研究生课程 | 开课单位:数学科学学院 |
| 课程层次:本研贯通 | 学分:4.0 |
教学水平
张土生老师的《随机过程》课程整体上受到学生的好评,特别是在教学质量和内容安排上。课程进度适中,教学语言与教材一致,推导过程详细且严谨。部分学生建议课程节奏稍快,并希望能涵盖更多内容如随机积分等。此外,老师被普遍评价为和蔼可亲,讲课风格慢条斯理,易于理解。
课程内容
课程内容全面,涵盖离散和连续鞅论、马氏链、Poisson过程、布朗运动以及一般马氏过程等。尽管对测度论有一定要求,但大多数学员反馈通过课程可以很好地理解这些概念。部分学生建议在具体应用和实例上增加更多的讲解,以加深对概念的理解。
作业与参考资料
作业频率适中,内容涵盖Durrett和Le Gall教材的习题。虽然网上有答案流传,但需要注意答案的准确性。此外,学生建议利用多种参考资料辅助学习,如Revuz & Yor的《Continuous Martingales and Brownian Motion》以及Liggett的《Continuous time Markov Process an Introduction》等。
考试与给分
考试普遍被认为较简单,题目多来源于课堂内容和作业题,更注重理解和掌握基本概念。然而,助教的判卷较为严格,要求学生在解题过程中写出详细步骤。给分按照平时、期中、期末成绩比例划分(2:4:4),对此部分学生觉得评分严格,并希望有更多的灵活性。
总结
总体而言,张土生老师的《随机过程》课程评价较高,是一门适合希望深入学习随机过程的同学的课程。课程内容涵盖核心概念,教学风格容易跟随。对于测度论有基础和对概率论感兴趣的学生,尤其推荐选修此课程,对于想继续学习随机分析的同学,也是一门很好的过渡课程。
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:很多
看了一下24年的期末试卷,可以说质量非常好,需要一定的理解深度,尤其是前三题。T1算是Girsanov测度变换(这个变换在research中非常重要!实际上hoeffding ineq证明里面也有提及)在Brownian motion里最经典栗子之一,在这里实际上按定义test function展开变量代换一下就能出来;T2用常规的分析标准手法+BM最基本的性质就能解决;T3可以接着T1通过Girsanov测度变换后再构造鞅(martingale)利用标准方法解决,也可以利用T4的结论(legall貌似也有(类似的)作业题)做。如果只是硬背结论没有仔细思考课堂内容的话做前三题还是比较棘手的。另外conditioned on yss出卷结合授课和给分来看的话比两年半前的高钙确实长进了很多。
这学期刚好去北大旁听学习xwj老师的随机过程论,结合这门课原有的大纲和授课内容想再提点建议:这门课各部分的理论框架整体来说很完善,也把细节讲得很清楚,但这门课把超过八成的时间和精力都放在此了,对鞅,马氏链,布朗运动等的例子和应用讲得过少。我认为今后授课在这方面上还可以再侧重一些。
- 关于鞅,实用随机过程里比较侧重投骰子/花样问题,比如某个有限序列出现时间的expectation讲了若干方法,讲到鞅的时候给了一个构造鞅的方法,当然还有其他例子等等。我认为这门课也可以在这里简单提及一下,至少给一些经典且深刻的例子来加深对鞅的理解是很有必要的。实际上research中最困难也是最origin的点在于如何在问题情境中巧妙构造鞅或者差不多是鞅剩下可以被一个校正子控制等等,实际上这也可以看成一种coupling的方式,运用鞅的结论给出证明是standard,可能会涉及一些技术细节但应该不是最本质困难的地方。
- 马氏链在random walk的应用也可以再深入讲解(比如参考durrett5.4,5.5节),另外如markov chain的generator可以看作discrete laplacian一些和离散PDE相关的结论(这是lattice model里最基本的常识),我认为也可以在课堂上补充(lawler的intersection of random walk这部分写得很全,可以参考),与之对应的连续情况下亦成立:Brownian motion的generator就是正常意义下的laplacian。
- Brownian motion和连续鞅讲完可以额外上一节课或者开一节习题课专门讲讲legall那些习题,和课堂内容有个比较好的衔接。这几道题难度总体很大但绝大部分都是最经典的例子,否则很容易因为考前背答案然后考完试完全扔掉了(比如我。。。下面提及的Peter Mörters, Yuval Peres的Brownian motion这本专著算是精炼的BM百科全书,感兴趣着可以学完直接慢慢啃。
另外强烈安利一下你科网络课堂课程:王冠扬学长讲授的“马尔科夫链里的耦合方法”。其中讲了耦合及其相关的证明方法,mixing time,以及一些模型的栗子及耦合在其他学科(如统计MLTCS等)中作为算法的应用。耦合的具体实现往往也通过构造某种“算法”/regime来完成,里面的idea私以为是很概率的,比较适合作为本课程的衍生内容。
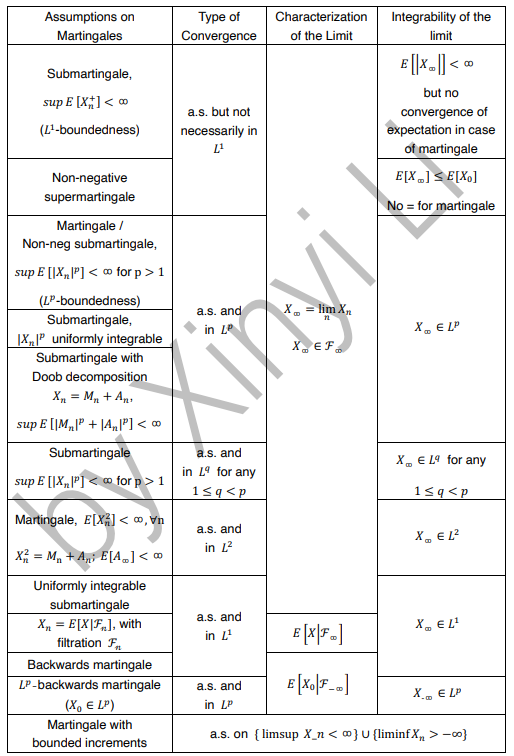
前段时间看到一个关于鞅收敛结论总结的outline,感觉比较完整了,在这里扔一个。事实上从分析角度看某种意义上similar with Hardy-littlewood极大函数的结论(包括一丢丢similar with插值定理的idea)
给概率壬推荐一些这门课衍生出的参考资料:
布朗运动是现代概率论中非常基本且重要的模型,里面涉及到的很多问题和idea对于今后研究纯概率领域都是非常有帮助的。这里非常推荐Peter Mörters, Yuval Peres的Brownian motion专著 Brownian Motion.pdf,甚至可以尝试完全啃下来。
durrett5.4节后半部分讲了在Z^d上更general的random walk探讨了不同d下常返性的条件,里面用的证明技术都是basic的概率和分析,值得一学。另外若深入了解随机过程和马氏链理论,尤其是离散概率这部分,入门的话先可以看一下p大陈大岳老师的自编教材《应用随机过程》随机过程_陈大岳.pdf(请注意,这门课在p大是具有相当历史的硬课,跟你科翟应随完全不是一个量级),里面也给了不少参考资料(对(modern/群上的)随机游走理论感兴趣者教材里都有推荐)。此外,想学习 mixing time相关的内容(尤其是直接尝试对标research的话)非常推荐Levin-Peres-Wilmer 的Markov Chains and Mixing Times Mixing Times of Markov Chains_ Techniques and Exa.pdf。可见大佬Yuval Peres不仅概率论research做得很顶流,而且writing也非常之好,值得钦佩。大佬主页上自己编写的各种专著都很推荐大家去看看。
此外,对随机分析感兴趣可以看看Martin Hairer的SPDE讲义 SPDEs_Course.pdf 写得非常好,涉猎了很多topic,非常值得一读。
张老师大善人!!!
授课内容基本与往年大纲一致,进度适中。这门课风格和本科应随完全不同,整个内容是在高概语言基础上建立而成,抽象程度和语言严格化上都比应随做了更高的要求。老师基本上把每个知识点中最核心的部分都讲得很清楚也举了实例,而不像应随一样沉迷于各种寄巧和小结论(像这里布朗运动讲了零一律以及通过反射原理得到sup_Mt/停时T_a的分布后就可以a.e秒杀应随里的一些小结论)
老师上课节奏很舒适,很流畅,板书也非常清晰,推导过程中遇到难点时也会反复解释。总体来说体验效果很不错,也算比较标准化的授课模式了。
可能是因为老师不久前从英国回来,第一次在国内正式授课而不太了解国内高校学生的授课情况(总体国外高校课堂活跃度越高于国内),所以考(gei)试(fen)十分水(lao)!期中大部分是原题而且原题难度也不高,特别送。期末没期中那么送,但也不难,只要把基本概念理解清楚,作业题和笔记好好看,考试把细节注意好就能拿到高分。
给分比例是平时:期中:期末=2:4:4。我期中有一道很简单的马氏链题目翻车了,94;期末100,最后总评98!感谢张爷爷让我拿到妮可首个数学课期末卷面满分和最高数学课总评!
总之大力推荐!
- 课程难度:中等
- 作业多少:很少
- 给分好坏:一般
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:一般
- 收获:很多
这学期去得最多的课,终于结课了。好像翘的课次数和本科某门必修课去的次数快一样多了。课还是很不错的,尤其是在同行衬托下。不给10分是因为觉得不够精彩,仅限于不错,能学到东西,而且有用,建议都选,早选。
传一个notes供参考,文件很大。goodnotes压缩也压不动。home.ustc.edu.cn/~matchbox/ASP_notes.pdf
这是一个总结性的大纲笔记,可以转成思维导图。https://www.mubucm.com/doc/7rUU6LCTrMB
关于课程学习,算是比较舒适,老师上课节奏把握得不错,让人有些听的欲望,摸一会鱼也能跟得上。
先简单聊聊课程内容。老师基本是完全照着书讲,但是听课会比自己看书舒适很多,课堂也会有一些不明确的内容,自己看书补上效果更好。有些内容我也理解得不够透彻,如有错误或不恰当的地方望指正。
期中前:
- 离散时间鞅和离散时间马氏链。这一部分算是一个入门,学到后面再看会很容易,因为后面连续的内容大多使用离散的逼近。难点在于不会高概(球球数院好好开高钙):测度论都不太会,比如什么直接用单调类定理不妨只证明,每次只能承认,或者花很久用一个牵强的理由把自己说服,也不算难吧。还有条件期望,和用带有Filtration、stopping time的语言来刻画鞅和马氏链等等。但归根到底只是一个“语言”上的难度,熟悉了以后就好很多。后半学期听说本科某课也在讲鞅,但没讲filtration??还是叫什么关于 \((X_1,\ldots,X_n,\ldots)\)的鞅?甚至stopping time只是提了一下,证明完全没有,没有让同学看到这一工具的强大性,不知道意义何在,大三的学生干嘛要学那一套鼓捣条件概率,有一份好讲义高中生都能算明白的东西?当然,很多同学学那门课算不清条件概率,数学系的同学确实不会喜欢那些繁琐无聊的东西,讲义也不行,被这门课内容吊打。
期中后:
- Poisson过程:这部分张老师只用了一节课,但我觉得讲的东西足够了。看见那门课的小o就烦,放过我吧……
- 布朗运动:作为连续时间鞅的代表,也能产生连续时间鞅,提供了很多例子,理论证明也相当漂亮。从定义到构造到\(\sigma\)代数\(\mathcal{F}_{0+}\)的01律再到作为应用的一系列轨道性质,最后介绍强马氏性,整套下来一气呵成,完全碾压那门必修课。
- 连续时间鞅:这部分就是把离散时间的结论通过逼近再走一遍,没有太多新的思想,但为了这门课的完整性也是必须要了解到东西。那段时间因为事多也翘了几次课,书上定理证明写得很清晰,可以看一遍。
- 一般马氏过程:课程最后最精彩的部分,一次迟到到教室看到一堆堆算子和“预解式”,Resolvent identity?\(R_\lambda-R\mu+(\lambda-\mu)R_\lambda R_\mu=0\)以为是错走进了泛函分析的教室。还好泛函没学好不怎么影响这部分的理解,我也无法解释泛函对于随机过程的作用究竟有多大,希望最后能学明白吧。这部分的顶峰大概是研究在一般的转移半群和Feller半群下不同的研究工具:(Feller)转移半群\(Q_t\)、预解式\(R_\lambda\)以及无穷小生成元\(L\)(对,就是某门必修课连续时间马氏链要算的那个G)。这里其实看起来蛮tricky的证明背后的观点都不难想到:\(Q_t\) 便代表转移概率,预解式\(R_\lambda\) 是转移概率作用到某个有界连续函数上的Laplace变换(其实这里直到复习本科那门必修课我才想明白背后的原理,所以那个课也不是一无是处),\(L\)是\(Q_t\)算子在0处对\(t\)的导数,对于位置坐标\(x\)来说大概是一个二阶微分算子,从布朗运动这个例子中得到的\(Lf(x)={1\over 2}f''(x)\)可以明显感觉出来(本科那门必修课似乎也提到了布朗运动的转移半群满足热方程,但证明方法只是简单的分别对\(t,x\)求导验证,我想大部分同学应该不会懂得其背后的含义,当成一个不知所云的课后练习题)。第一遍学的时候还会学到一个令人惊奇的性质:预解式作用在\(Lf\)上,大概等于\(f\)(相差一个带常数的项):\(R_\lambda (\lambda-L)f=f\)。我个人理解这其实就类似数学分析学的对于一个导数\(f'\)作Fourier变换,结果等于一个数乘以\(f\)的变换。这种积分求导与乘除法相互转换,正是Fourier变换与Laplace变换最精彩的性质之一,体现在这里便是\(R_\lambda Lf=\lambda R_\lambda f\)。然后课程用这些工具(线性算子)来刻画马氏性、强马氏性以及分析马氏过程的一些性质,比较精彩的是几个“鞅性”。整理下来收获颇多。课程的最后简单介绍了跳过程和Levy过程作为马氏过程的两个例子,跳过程本质是一个马氏链,核心是证明出来\(X_{T_1} \)和\(T_1\)独立,然后算一些具体的算子结论。Levy过程也是经典且一般的随机过程,平稳独立增量大概可以使它涵盖布朗运动、Poisson过程等。不过张老师对于Levy过程转移半群的Feller性质好像说的不太明确,至少没有明确把\(Q_t(x,A)\)的可测性证明出来,而书上将其作为强连续性的推论,也是个有趣的想法。到这里,那门屑必修课的内容除了最后的随机积分应该被完全涵盖了,而且是降维打击。
- 个人认为随机积分也是有点用的,这门课限于课时没有讲到,不过没有遗憾,反正有门必修课逼着我学。
值得一提的是期末考试变难了,不再像之前的评价和期中那样纯放水(一眼看过去所有题都会做不到一小时写完交卷)。但也不太难,鞅论复杂的定理证明都可以完全不会,会用就能考。最后一章一般马氏过程学起来蛮有趣的。期中期末拿高分都挺难,这学期助教似乎是依据步骤和关键词给分,这一点不太能理解,可能就是期中期末把所有题都做出来最后都不到90分,不过也无所谓了,差不了多少。
一学期的作业全都有答案,每次很快就能抄完,想看懂的话可能得多花点时间(完全不会自己写作业的)。这和其他课比起来也舒服得多,毕竟大三下没什么时间上课写作业。
总的来说,这门随机过程与本科某门类似名字的屑课相比,含金量大得多,尤其是鞅论的内容。马氏链的知识我觉得如果不做相关领域,只知道个马氏性和平稳分布也就差不多了。偏理论的learning的paper中也可以看到鞅论的应用(主要是停时,鞅收敛等的直接应用),我所知道的最著名的是关于线性bandit的2011年最经典的一篇paper: Contextual bandit with linear payoff functions. 这篇文章引用量近1000,然而它最伟大的贡献便是将鞅论引入到了bandit理论的研究之中,摒弃了之前抽样独立同分布的错误做法。从那以后所有关于这个话题的文章都在引它。引的就是一个用了停时证明鞅收敛的定理,由此得到某个形式的concentration bound。所以学起来感觉似曾相识,又会有很深入的理解。之前和做统计的老师交流,他说学好鞅论读统计的paper会顺利很多,我没读过什么统计文章不作太多评价,只知道有关鞅和鞅差序列的concentration inequalities也相当有用。这些都是那门课完全做不到的。
最后,不装了,我就是来黑应随的,祝它早日被高级替代,当然这需要后来者的努力。
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:很多
老师是刚从英国回来的概率学家,人非常可爱:)
虽然老爷爷讲课慢条斯理的,但本人觉得收获还蛮多的,建立在高概基础上的这套严格语言真的比本科生随机过程学起来舒适多了。
贴下老师给的课程简介里的信息:
教材:
Durrett - Probability: Theory and Examples, Version 5 (PTE5_011119.pdf)
Le Gall - Brownian Motion, Martingales, and Stochastic Calculus
授课计划:
第一周 - 第四周: Durrett, Chapter 4, Martingales
第五周 - 第七周: Durrett, Chapter 5, Markov Chains
第九周周二: Durrett, Section 3.7, Poisson Processes
第九周周四 - 第十一周: Le Gall, Chapter 2, Brownian Motion
第十二周 - 第十四周: Le Gall, Chapter 3, Filtrations and Martingales
第十五周 - 第十六周: Le Gall, Chapter 6, General Theory of Markov Processes
(本学期老师应该是完全按照这个计划完成了教学,让我想起上学期yss高钙学期初画的饼与现实的巨大差距,令人感叹,,,
- 课程难度:中等
- 作业多少:中等
- 给分好坏:一般
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:一般
- 收获:很多
教学水平
个人认为颇为一般,张老师上课完全就是在抄自己的讲义,比较无聊(部分原因可能是老师年纪大了?)。由于到每年内容基本相同,且本课程无点名,可以考虑自学教材或pksq的笔记。
课程内容
每年内容基本相同,前半学期主要讲Durrett的4-5章(去掉带*内容)和3.7节的一部分,后半学期主要讲Le Gall的2,3,6章。其中部分偏测度论的内容(比如Markov过程的构造)会简略讲讲或一笔带过。此外今年因为进度较快,老师最后紧急刹车(提前下课)也没刹住,所以多讲了一点点Levy过程的内容,不过考试并不考察。
作业
前半学期留Durrett上的习题,共5次,每次5-9题;后半学期留Le Gall上的习题,共3次,每次3-4题。这两本书在网上均有习题答案流传,可自行搜索(注意网络上的答案可能有误)。
作业难度总体不大,但考试可能会出原题或改编,需掌握的牢固些。
考试
期中和期末都较简单,基本都是作业和往年考试原题及其改编。但听说今年期末改卷较严格,因此答题时需要足够细心,把过程写严谨些(不要考完才意识到题看错了,寄)。
给分
总评=平时(20)+期中(40)+期末(40)。
今年是按照给分公式出总评,一分不调(好像会捞卡绩的?)。考虑到考试较简单,因此只要把基础知识掌握并考前复习了,就能取得一个不错的成绩。但如果想要拿到一个较高的成绩(比如95),容错率不大。
总结
由于课程内容固定,作业不多并且有答案,pksq上有同学记的笔记(伟大!),考试较为简单,这门课已经部分成为了一门水课。当然,如果想要学好(而不只是混个学分跑路),仍需花费不少时间和精力。
对于概统方向的同学而言,可以考虑大二秋学习刘率论,寒假预习一下实分析,即可学习本课程(当然也可以预习一下实分析和Durrett,去学隔壁的极限理论),bc。
- 课程难度:困难
- 作业多少:中等
- 给分好坏:杀手
- 收获大小:很多
- 难度:困难
- 作业:中等
- 给分:杀手
- 收获:很多
期末回忆卷:final.pdf
一门内容选择与教学都非常优秀的概率研究生课。
我们先来回顾这门课讲了什么:
- 离散鞅论:鞅的定义与基本定义、停时、离散随机积分、\(a.s., L^1, L^p\)-鞅收敛、在 \(L^1\)-鞅收敛中带出了一致可积鞅以及可选停时定理
- 极限理论课中,胡治水老师用逆鞅整了一些绝活。Durrett 上的 4.3、4.5、4.7 节值得一看,其中的例子很有意思。
- 离散时间离散状态马氏链:马氏链的定义、构造 (基于 Kolmogorov 相容性定理)、马氏性与强马氏性、状态分类 (常返态与暂态、其中夹杂了很多对首中时等的讨论)、平稳分布
- 总的来说离散的部分并不十分困难,没有什么细枝末节的讨论,也很符合直觉。但 Durrett 确实是完全不适合自学的一本教材 (过于简略跳跃的定理证明),所以我参考了一些笔记进行学习:一个是 24 春评课学长的笔记 https://icourse.club/course/24550/#review-84480、另一个是知乎大佬的笔记 https://huarui1998.com/Notes/math/prob_2024.pdf。
- 中场过度 (连续时间随机过程的典例):泊松过程 (最经典的独立增量计数过程,提到了基本定义、基于指数等待时间的构造也是另一种定义、合并与分离、计数点在条件下服从均匀分布的次序统计量)、布朗运动 (从准布朗运动入手并进行连续化修正的构造、离散逼近连续思想、一些轨道性质、Blumenthal 0-1 律、马氏性与强马氏性、反射原理)
- 泊松过程土老师花了一节课就讲完了,但其实也讲差不多了。更加系统细致的讨论或许可以参考本校应随以及北大陈大岳老师的应随讲义。
- Le Gall 书上提到的另一种构造布朗运动的方式——Winner 测度——值得一看,Le Gall 书的自学体验暴打 Durrett。
- 连续鞅论:定义与构造鞅的基本方法 (划重点指数鞅)、停时与滤流、连续化修正、右连续鞅的各种收敛以及可选停时定理
- 连续情况的停时与滤流和离散会有挺多区别的,主要体现在 annoying 的可忽略集、以及 \(t, t-, t+\) 的区别上,为此也一下引入了挺多概念,初见略显茫然。但最后给出了漂亮的结果:“在滤流是右连续且完备时,循序可测过程的任意 Borel 集的首中时都是停时”,而右连续过程便是循序可测过程的最经典特例。
- 对于停时 \(T\) 的前滤流 \(\mathcal{F}_T\),其实有诸多学问,需要直观与抽象并用去理解。胡治水老师在极限理论课中也有提及。
- 连续化修正后就和离散鞅无二致了,用离散逼近连续即可。
- 一般马氏链理论:转移半群、马氏链定义、Feller 半群、预解式、生成元、利用生成元构造的鞅、马氏性与强马氏性、典例 (跳过程、Feller 过程)
- 在预解式和生成元这一部分和离散马氏链画风有显著差别,我至今还未完全参透其内核。除了从 Laplace 变换的角度理解预解式,其是否还有别的解释,最好有直观的解释?生成元也同理?离散马氏链中是否有对应的概念或方法?利用生成元构造的鞅很漂亮,但动机与应用是什么,离散中是否也有?貌似应随中提到的离散马氏链的生成函数与其有些关系,我没上应随,不太懂😂
- 跳过程泛化了几乎所有的连续时间离散状态马氏链,指数闹钟模型从泊松过程下来一脉相承。更细致的讨论亦可参考本校应随以及北大陈大岳老师的应随讲义。
作业不多,期中之后更是过好久才要交一次。但挺初见杀的,应该是第一次系统接触随机过程,有些题目第一眼看过去没什么思路 (这一点在离散时更明显,到连续的时候已经有了离散的直觉)。抄答案的候注意一点,市面上流传的 Durrett 与 Le Gall 的答案都有一些错误,甚至有的题目完全就是错误的解答。不得不提的是一位助教在写作业解答的时候可以说是完全照搬错误答案,似乎没有自己的思考,高概时 TA 也是这么干的,令人费解。介于研究生可能不是自愿当的助教,我也不多说什么。
考试土老师都是一如既往的放水的,弄懂作业和上课内容 (基本定理的证明其实完全不需要掌握,只要会用),两次考试都是最低最低 80 分;随机看一点往年卷或许就可以攻破剩下的 20 分。这几年土老师的试卷难度应该是在一点点变难,但都控制在合适的范围。唯一的奇点是 24 春时杨赛赛老师代课出的卷子,几乎不送分,每一题都是中档题,整体难度较大。
科大概率课程的体验都是极好的啊,回想起来从大二下跟着刘党政老师学习概率后,陆陆续续学习了一些概率课程了:高概、随机过程、极限理论、算上统计还有数理统计和回归分析,每一门课都让我受益匪浅。虽不是数院管院的,但仍然不后悔自己跨院选修了这些课程。感谢所有让我领略概率美好的老师们!
一点小碎碎念,期末考的 T5,设鞅为 \(M_t = \exp(A) + \exp(B)\) 的话,直接用可选停时定理得出的式子是 \(2 \cosh(A) = 2 \cosh(B) \cdot \mathbb{E}[e^{-\lambda T}]\)。我两边少写一个 2,除此之外没问题,二十分题扣了十分。
这题是作业原题,理应完全掌握,只能说助教们判卷怎么扣都合理,但总是感觉比较不爽。在 244 给分几乎雷打不动的情况下,给分好坏确实完全取决于助教的判卷力度。
但我也不会因为这个去更改我对这门课的评价,毕竟评价一门课应该从传授知识的好坏与多少评判。
给分是中规中矩的 244。因为期中期末的严苛改卷让我越想越不开心,所以把给分下调为”杀手“来表达一下自己的小情绪~
- 课程难度:中等
- 作业多少:中等
- 给分好坏:一般
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:一般
- 收获:很多
隔壁极限理论gg了来这评下课。个人很喜欢老师的上课节奏(或许可以快那么一点点),期中考考的离散时间鞅和马氏链,作业题掌握就不大有问题。(但是过程要求挺高,鞅没验证可积都得扣一分)
期中后内容感觉明显变难了,期中考占百分之四十应该只是调分(捞人)的一种手段吧,等考完期末再来评。(研课期中考难度亦有差距,特别是有的课还用开卷来羞辱你)
期末出分评:期中后内容有同学已经评价得很完整了,不再赘述了。作为一个从头听到尾的人,我确实感觉上完课对这些知识点的理解还是很有用的,复习也轻松很多,体验很好。意外的是期末我有9天复习时间,本以为没啥问题了,结果上来有个鞅忘了怎么构造想了半天才搞定,后面提前交卷又发现有个地方没说好,心惊胆战了很久。(其实都是legall原题)这其实也说明概率相关的东西还是得把细节什么的都理解到位会更好一点。
查卷更新:助教改卷挺严的,T2有个小地方|B(0,1|/n^(α)趋于0 a.s我直接显然扣了6分。还有笔误扣了一分,以及最后一问写得不太好的问题。只能说概率这块想不被抓到小错误还是得多加小心。
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:很多
土老师大善人!
虽然本壬未曾想过走概统方向,但因为受到了ldz的推(gu)荐(huo),还是在大二下选修了这门课。整体感受十分舒畅,但可能是因为没有上过某应随,马氏过程那块直觉十分有限,许多结果理解起来还是有一点困难。提前选这门课的同学或许双开应随或者提前看一下初等的书会更好。至于高钙,并没有本质上用到多少,毕竟你可以直接承认许多大定理。
课程内容前人之述备矣,不过还是觉得土老师可以讲快一点然后把随机积分覆盖掉。
这门课作业还是有一定难度的(吐槽一下网上那份 le gall 的答案写的不太行),但考试十分白给,改卷对于过程的要求十分严格(严格到让人怀疑这是不是数学考试)。
今早查其他课成绩时发现这门课也出分了,期中98,期末100,总评100,感谢土老师给了我入科以来首个满分总评!(zlf欠了我一个,笑)
- 课程难度:中等
- 作业多少:中等
- 给分好坏:一般
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:一般
- 收获:很多
一门很优秀的概率本研课,具体授课内容别的评课已经写的很多了,在此不再重复了。
我一直觉得这门课是一种语言,主要是使用高等语言去描述了一些东西,对于具体解决实际问题并没有太多提及,所以还是比较推荐大家比较早选这门课的,大二下有实分析基础,定加上承认单调类定理,kolmogorov扩张理这些就可以去选这门课了,考试的时候涉及的测度论基本也都是实分析范围的。然后还比较推荐和应随双开,学习理解的时候以研随为主,应随作为例子补充(比如离散马氏链遍历理论和跳过程这些)。
今年一年都是土老师上课,总体体验较好,上课讲的比较缓慢(虽然我一开始鞅一致可积那块就开始晕,主要是实分析基础太差),后面从离散过渡到连续反而觉得比较自然了。马氏链那块转移半群预解式生成元由于没学过泛函直到现在也不是很清楚,只能说都知道是什么了。作业的话可以去综合各个版本的答案,两本书都能找到好几个版本的答案(当然错误都挺多的)。
考试的话,今年期中期末都非常简单,可能期末最后一问稍微需要思考一下,其他基本都是一眼就有思路的题,如果是土老师上课的话,应该基本就是这个难度。
当然今年助教确实挺神秘的,感觉作业改的极其松,考试改的极其严,幸好我属于过程写的比较细的,基本没怎么扣大分。
给分的话应该是244基本不调,而且好像作业也是严格给的?(不过作业批的非常松,对着抄基本都满分),本人期中98期末94总评97,学完这门课也让我产生了学随机积分和随机方程的兴趣,其实比较期待土老师多讲一点随机积分的内容的。
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:很多
迄今为止感觉最舒适的一门课
又到一年选课时节,发现选课人数比去年少好多,感觉需要澄清一些混乱的声音。首先随机过程现在课程程序渐趋固定,半学期Durrett和半学期Le Gall基本上不会改变,这两本教材都是非常好的,作业质量也很高,甚至于没有布置为作业的习题也十分值得一做,可以弥补一些课程例子不充足的缺点。这些作业,尤其是Durrett的部分,想要独立完成而没有错误相当困难。我在网上找到的所有答案都有极多或小或大的错误,远古评课社区一位学长留下的答案甚至可以一次作业每题都有错误,相比之下有一位助教给出的答案已经是非常完善的了。另一位助教手写作业答案,所以我没有仔细看过。由此也可以看出学习随机过程的特点:一个零测集不会改变结果,但是千变万化的零测集留出了巨大的伪证空间。对于所谓严苛的改卷和给分,如果做到了能发现每一处细微的谬误,那么断不可能在简单无比的期中期末考试当中丢失大量分数。事实上期末改卷的离谱标准确实有一处,就是已有同学提及的等式两边同时约去2会扣分。但是其它地方的标准合情合理,很多同学自以为显然的结果实则绝非显然,而我在查卷的时候就发现有两个同学在拿着错误的答案同助教据理力争。看到这样难度的期中期末还觉得需要调分只怕是习惯了微分方程等某些课程乱改卷再大调分的模式,但是改卷乱的前提在此其实并没有成立。只要认真学习,这一定会是一门轻松愉快而收获颇丰的课程。
- 课程难度:简单
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:简单
- 作业:很少
- 给分:超好
- 收获:很多
这是一门讲课很宜人而且考试比较轻松的课。老师十分可爱且温柔。待有闲工夫的时候填坑。
前人之述备矣,不想填了。笔记没准哪天会传到个人主页上。简略些的话,大概就是要说:“好!选!”
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:很多
张爷爷!爱了爱了!
这门课应该算比较硬核的课程了,但很多结论其实十分有趣,还有很多应用实例(不像另一门概统选修课,上着上着就迷茫地陷入一堆式子之中×)。
上课就是内容和书本完全一致,但老师每一步怎么推导都会很详细的解释,所以完全不用担心跟不上。人到大三下,这门课可以说本学期唯一一门能持续保持听课状态的课程了!
重要的是,考试炒鸡简单和基础,约等于课上知识点和作业题默写,完全不必担心考的不好。但要拿高分一些细节还是要留意。
课程内容与应随有重复,布朗运动和离散鞅论基本是真包含关系,对应随复习很有帮助。
我唯一感到困难的是前半学期durrent上的作业,经常一道题想一小时还想不出(呜呜喵),只能靠学长答案完成。。
所以,如果明年还是张爷爷,且考试难度不明显变化,强烈推荐选啊!(特别是与其他几门概统选修课对比)!(不过话说很多人今年没选这门课,是不是被上学期某门数院研究生课老师搞怕了的缘故,呃呃呃~~
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:很多
中规中矩的课,没有太多亮点也没有太多槽点,内容也都是随机过程入门的标准内容。等其他课考完试我可能会把自己整理的笔记传上来,供交流学习。
教材的话,durrett第四第五章应该是拿来学习离散鞅论和马氏链的标准内容。不过也有一些槽点,例如第四章压根没提停时对应的sigma域然而课后题里却出现,第五章很多符号压根没解释就拿来用,疑似是书再版增删内容所导致,读的时候注意一点就好。布朗运动,连续鞅,连续markov过程用的是GTM274。这书优点是特别好读,内容简练,废话不多。不过深度可能就欠缺一点,例如连续markov过程那里就很草率,可能要自己专门找书去看。
另外再推荐几本教材:
Continuous Martingales and Brownian Motion ,by Daniel Revuz & Marc Yor
应该说是GTM274的升级版,前三章涵盖了布朗运动,鞅,马氏过程的基础知识,但讲的内容更多一些。(实际上GTM274上好多课后题是从这里摘的)后面则是随机分析的内容,非常好的一本书。
Continuous time Markov Process an Introduction,by Liggett
讲离散状态空间上连续Markov过程,也就是应随里面那些内容,只不过严格化了。第二章讲从两个角度构造Markov过程(迭代法求解Kolmogorov向后方程&直观的概率方法),第三章则是Feller过程。比Chung,Freedman写的经典教材容易读很多。
Foundations of modern Probability,by Kallenberg
很有名的一本字典式专业书,内容多且艰深。不过这上面关于随机过程章节写的都很不错,感觉第6,7章(鞅,Markov过程),11章(Gaussian过程,布朗运动),13章(Levy过程),17章(Feller过程)都蛮值得一读,作为补充参考也很不错。
最后,这门课考试灰常灰常的水,期中期末我都一小时交卷走人了,虽然还是被扣了海量步骤分,但最后也摸了一个97,心满意足。(感觉张老师有点摸不着学生的底细,他上课时常会提问一些很容易的问题,然鹅底下无人应答,可能老师据此降低了考试的难度。然而事实上大家似乎只是不想说话。)
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:很多
其实老师还是小调了一下分的。这门课的期中期末都相当的送,理解了(背住)上课和作业题就能拿到相当可观的分数,新题基本上都是验证类的题目,完全没有需要技巧的题目。
不过判卷相当严格,期末第一题直接使用结论(假设在一个速率为 \(\lambda\) 的泊松过程中,每个事件以概率 \(p\) 被保留下来,并记 \(\widetilde{N}_t\) 为到时刻 \(t\) 为止被保留下来的事件总数。 则 \(\widetilde{N}_t\) 是一个速率为 \(\lambda p\) 的泊松过程)被扣了5分,所以大家能写全还是写全,不要偷懒。
老师似乎捞了一下卡绩的同学,其他的可能就是严格244了。不过这课听起来也没啥压力,考试也简单,选就完了。
- 课程难度:困难
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:中等
- 给分:超好
- 收获:很多
感觉是数院概率本研贯通课里面上的最好的一门课程了。
关于这门课程,个人认为内容和体验上都爆杀应随(除了少了一部分随机积分);之前有没有学习过高概并不是很重要,因为老师在前几节课会把要用到的内容讲一下,不过如果熟悉了高概的语言的话,对于条件期望这些内容的理解会顺很多。
个人认为前半学期课程的难度主要在鞅上,不过幸好期中考试真的非常白给,平时有好好的看作业题基本就能全部写完;后半学期无论是布朗运动还是连续马氏过程刚开始学习的时候都觉得很难,不过到最后熟悉了内容后回过头看就不是那么困难了。
Btw,因为数院ntjwc不能用随机过程高等替代应随,十分建议学习应随之前首先学习随机过程!尤其是应随变成三学分后,真的是什么都讲了,但是什么都没讲。并且随机过程上课体验、考试和给分都很友好。
总之,这门课1000%的推荐!
- 课程难度:简单
- 作业多少:很少
- 给分好坏:杀手
- 收获大小:很多
- 难度:简单
- 作业:很少
- 给分:杀手
- 收获:很多
土老师老师讲课不快,颇有一种养生之感;讲解内容浅显易懂、思路清晰、娓娓道来,证明慢条斯理、步骤严谨,板书干净整洁;为人和蔼可亲,坐在前面有时候还会聊上两句;考试多为原始定理命题证明(或作业)和类比,简单轻松。
这门课是开在春季学期的课程,上学期如果选修ldz的概率论的话他可能没事就给你推荐这个zts的随机过程(我就是这么来的)。虽然是研课,但是内容并不困难,感兴趣的同学完全可以放心选。不过该课程需要相当的测度论的基础,诸如0-1 law,Kolmogorov Extension等,完全不会的话会导致一些内容无法理解,因此建议大二下选课的同学最好提前学习一下测度论,理解定理即可(反正实分析也要学)。
上课当然是没有点名的,不过这个课听一听也蛮有意思,比之自学舒服很多(虽然讲得很慢吧)。今年的课程内容为:离散过程鞅+马氏链,Possion Process与Brownain Motion,连续过程鞅+马氏链,Levy Process(这部分不考)。期中考试后作业难度小幅增加,同时可能还撞上其他置课的考试,可能需要合理安排学习时间。
本来是毫无疑问的好课,不过这个阴间批卷确实好笑,在我证明没有遗漏和错误的情况下能给我扣这么多分,加上244一分不调刚好卡绩,但凡少扣一分都能绩点+0.3,虽然无伤大雅但确实很搞得人很难受了。在此给以后选课的各位同学一点建议:使用交换次序定理时要把用的定理名字写上去;使用马氏性以外的公式时把原始公式抄在一旁;使用无穷维向量时要在旁边指明;有时间的话对你使用的显然的结论加以证明;等等(恕我想象力有限,只能根据自身经验提出这些建议了)。
另一方面,某助教给出的作业答案貌似也有问题(不过我后面就没有看了),pksq传的那个elegantbook敲的讲义也有一些问题,大家理性使用。
不过选这课的目的本来就是来科普了,也着实学到了很多东西,感觉不管是不是概统方向的同学都可以来听 ( Ciallo~(∠・ω< )⌒★