2025秋 2024秋 课程号:PHYS5005P02
- 课程难度:困难
- 作业多少:中等
- 给分好坏:一般
- 收获大小:一般
| 选课类别:基础 | 教学类型:理论课 |
| 课程类别:研究生课程 | 开课单位:光学与光学工程系 |
| 课程层次:本研贯通 | 学分:4.0 |
- 课程难度:困难
- 作业多少:中等
- 给分好坏:超好
- 收获大小:没有
- 难度:困难
- 作业:中等
- 给分:超好
- 收获:没有
调整为2分。
这司马作业真是太阴间了,再补充一点,修读这门课请保证精通场论
别想着龚明能给你讲明白任何一点东西。
作业写破防了,以后有空来补充。
省流:非常非常不推荐,看似囊括很多内容但实际上没有讲清楚任何一个专题。
先叠个甲,我理解每位同学的知识储备、接受能力都是各不相同,想让一门课程做到所有人都满意也不太可能,不排除有同学在这门课上收获了很多,比如说对物理图像更清楚的认识。所以我只是作为一名在之前没有相关课程基础并且自学能力也不强的同学,说一下到目前为止的上课体验.
这门课所用教材是Sacdndev的quantumn phase Transitons,我可以说这是我体验感最差的一点,这本书非常非常不适合给高等统计物理这门课做教材. 只拿第二次作业涉及到的重整化群部分举例吧,我不相信任何一个新手能通过看这本书学懂重整化群,书里诸多的概念和公式都像从天上掉下来的一样,让人完全摸不着头绪,就像下面讲到RG的费曼图方法的时候:

这图就这么直楼画出来了(?),我清楚地记得老师大概用了半节课的时间讲这俩图怎么画出来的,而且忽路了其中的参数计算,非常唯象+半定性的给出来一个结果. 给我的另一个感觉就是,老师的讲课和这本书一样让人提模不透,而我选一门课的目的肯定不是为了猜谜. 为了赶这第二次作业我去找了很多量子统计物理的书,把里面讲重整化群的部分仔细读完才大概明白这样操作的意义是什么.
另外就是书里的小错误很多,比如作业4。2题的(3):证明的\(O(N)\)对称性系统的RG流方程的不动点在一阶情况下变换矩阵的本征值. 这恰好就是书里第四章讲的模型,但抽象的地方是,它让证明的\(\lambda\)和它正文里写的结果对不上,去问助教得到的回答是他也觉得很奇怪(乐),再比如下面这个精确到\(\epsilon\)一阶项的线性化方程:
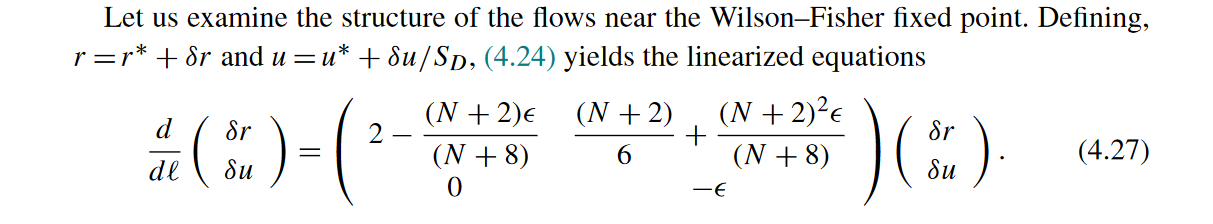
我算出来的右上角的矩阵元第二项系数少一个\(1/12\),不知道有没有人和我一样,总之书里这种让人疑惑不解的点实在太多了.
老师好像非常强调物理图像,在第一堂课乃至之后的课程上经常介绍这本书的一大特色之处是全书都是围绕 Ising model 和 Rotor model 来展开,非常新颖,但也不止一次提到这本书极为难懂,讲课大概就是尽量把里面难懂的东西解释一下(还没解释清楚),所以说,一定非要选这样的一本书来当教材吗?
而且老师似乎很喜欢这本书里这种“看”、“猜”结果的思路,直言自己当学生的时候总是关注细节,而那些厉害的人在做计算以前一眼就能看出来答案,不需要去算,而这就是物理内涵所在. 我认同物理图像的重要性,在计算以前应该把握全局,但是初次接触相关内容就缺少严谨性,只能说非常不合理,我想老师自己如果没有做学生时候对计算细节的深究,根本无从谈起什么把握宏观的框架,有也是空中楼图,没有根基的啊.
按照教务系统上对这门课的介绍:
推荐几本我这几天读过的,感觉不错的教材:
- 《量子统计物理学》杨展如 最近读得最多的一本,推导详细,物理图像解释得很清楚,但关于RG群的费曼图技术那里讲得也一般,有些东西没有交待好,并且有一些小错误看得时候要注意一下.
- 《统计力学》黄克孙 很有名的书了,而且上面那本主要参考的就是它,很多图和公式都一模一样,可以对照着看吧.
- 《量子统计物理》王先智 去年刚出的新书,内容非常丰富,而且包括了不少非平衡态统计物理和流体问题的介绍.
- 《统计力学》帕斯里亚 很古早的一本书,有些地方可能写法比较过时,比如作者非常擅长使用特殊函数这一工具,我之前有一个\(d\)维积分就是在这本书上找到的. 不同的是它还介绍了一些统计力学发展的历史和宇宙热力学这样比较少见的话题,可以参考.
上面这些书的共有特点是涵盖了高等统计物理课程介绍提到的全部内容,并且推导详细,物理概念描述得清楚,因为我太废物,思维稍微跳跃一点我就理解不来,所以内容好坏不多评价,可读性一定很强.
总之,随便找上面的哪一本书做讲义,老师上课推导推导,效果肯定都比现在用的这本强.
- 课程难度:困难
- 作业多少:很多
- 给分好坏:一般
- 收获大小:一般
- 难度:困难
- 作业:很多
- 给分:一般
- 收获:一般
教材几乎无法自学,作业题目虽然题数不多但非常迷惑,需要花很多时间
感觉被选课系统的简介骗了,和实际内容完全不一样,折磨
成绩出了后补充一下分数一共参考,期末大作业是在提供的一些论文中(或者自选与课程有联系的论文),复现其推导过程和数据;上课有概率点名。我本人参与了1次点名(经常翘课不知道一共多少次名)且作业都做了(不保对),最终分数为81分
- 课程难度:困难
- 作业多少:中等
- 给分好坏:一般
- 收获大小:一般
- 难度:困难
- 作业:中等
- 给分:一般
- 收获:一般
赞同楼上观点,有意思的是这本书的前言里直接指出本书适合完成了研究生基本课程的学生深造所用。这里补充个例子,到第四章好多内容本废物都看不明白,于是掏出知乎开始找东云正树的量子速读想要有个大致框架(起码搞清楚概念是什么),结合gpt补了几天之后发现实际上我在想办法速成场论。所以这门课像极了刚上大学你的数学老师跟你说高中老师都讲过了我就不讲了,到大学阶段我们要学会新的学习方法balabala。总而言之,老师还是很有水平的,学者风范十足,这门课适合学有余力的大佬选修。