2024秋 2023秋 课程号:22900101
- 课程难度:困难
- 作业多少:中等
- 给分好坏:一般
- 收获大小:很多
| 选课类别:计划内与自由选修 | 教学类型:理论课 |
| 课程类别:本科计划内课程 | 开课单位:人工智能与数据科学学院 |
| 课程层次:专业基础 | 学分:4.0 |
本课程讲述离散数学的基本概念和理论,主要内容包括:(1) 集合、关系、函数等基本概念和理论;(2) 图论的基本概念和方法; (3) 代数系统的基本概念、几个重要的代数系统:半群、群、环、域、格与布尔代数;(4) 组合数学,其中包括组合存在性、组合计数、组合设计与编码以及组合最优化。(5) 数理逻辑,其中包括命题逻辑、一阶谓词逻辑、Her-brand定理和直觉逻辑。
教学水平与授课风格
邵帅老师的《离散数学》课程以其高水平教学受到广泛好评。他以循循善诱的方式,用富有逻辑且层层递进的讲解风格,使学生容易跟上其思路。课程设计上,邵老师注重启发学生思维,常以问题驱动学习,强调数学知识发现的过程和内在联系。不过,课程没有完备的教材或PPT,学生需要认真听课并结合多种参考资料进行学习。
课程内容
课程涵盖了抽屉原理、数论、群论、组合计数以及图论。内容丰富但较为紧凑,因其涵盖面广,同学们反应有时感到“学的东西多而不精”。数论和代数结构在课程中占据大部分时间,对图论的讲解相对较少,导致少数同学感到重心失衡。部分学生建议增加实际应用和编程练习,如RSA算法、图论应用等。
作业与考试
课程设有7次作业,满分120分,计算时作业部分取满分100。作业和考试题目多为上课例题和作业题的变体,难度适中但需要深入理解课程内容。期末考试卷面180分,满分按最低150分计算。整体考试难度较为多样化,但老师给分相当慷慨,优秀率较高。
给分与压力
本课程的总评计算比例为作业:期末 = 3:8,附加有分数冗余,许多学生即使在课程内容感到困难的情况下,仍能获得较高的总评分数。这给予同学们一定的缓解学习压力的余地,但有学生反映课程内容过于离散,复习时无从下手,尤其在没有期中考试的情况下,期末复习感到较大压力。
总体评价
邵帅老师的离散数学以高水准的授课和合理的给分方式赢得了学生们的赞誉。不过,课程的内容设计和教材支持尚需优化,以帮助学生在学习与复习中更有效地获取知识。该课程适合希望挑战自己思维能力的学生,但需要在上课和自学中投入较多时间与精力。
- 课程难度:困难
- 作业多少:中等
- 给分好坏:超好
- 收获大小:一般
- 难度:困难
- 作业:中等
- 给分:超好
- 收获:一般
“人有两件宝,双手和大脑,双手能计算,大脑能思考。”我相信对于科大的学生来讲,学习一门课程,尤其是数学课,不单单只是为了记下一些定理公式和解题套路,更多的还是要学会思考。这也是我希望大家能够通过这门课程的学习,通过自己亲自动手计算,动脑思考,能尝试了解并且掌握这些数学知识发现的过程,并且建立起这些知识之间的内在联系。
最后,我希望大家在科大这几年的学习过程中,能够真正收获学习的快乐(因为真的很快乐),变得聪明,而不是只有被成绩所支配的恐惧。
邵老师在有限时间内,从数学的角度,把这门压缩版课程(代数结构 + 图论,略去了较为形式化的数理逻辑)讲的非常精彩,同时能够充分调动学生自己动手计算、动脑思考,无疑是十分优秀的。但是客观评价这门课,其实与我的预期还有些差距。
数论和代数结构对将来学习密码学 / 形式化方法的同学较为重要;图论几乎覆盖所有主流技术领域,应用广泛,在算法设计中尤为重要。本学期大部分时间都在学习前者,对于图论最后只是浅尝辄止,重心略有失衡。同时,这门课作为 DS 和 AI 的必修课,希望能在课程中加入更多实际算法的应用 / 编程练习,比如RSA 算法、稳定匹配算法、网络拓扑设计、纠错码设计等,这或许会对我们更有帮助。如此看来,丁虎 老师的离散数学课堂似乎更符合我的口味。感兴趣的同学也可以参考 Berkeley 的离散数学入门课程:Discrete Mathematics and Probability Theory。
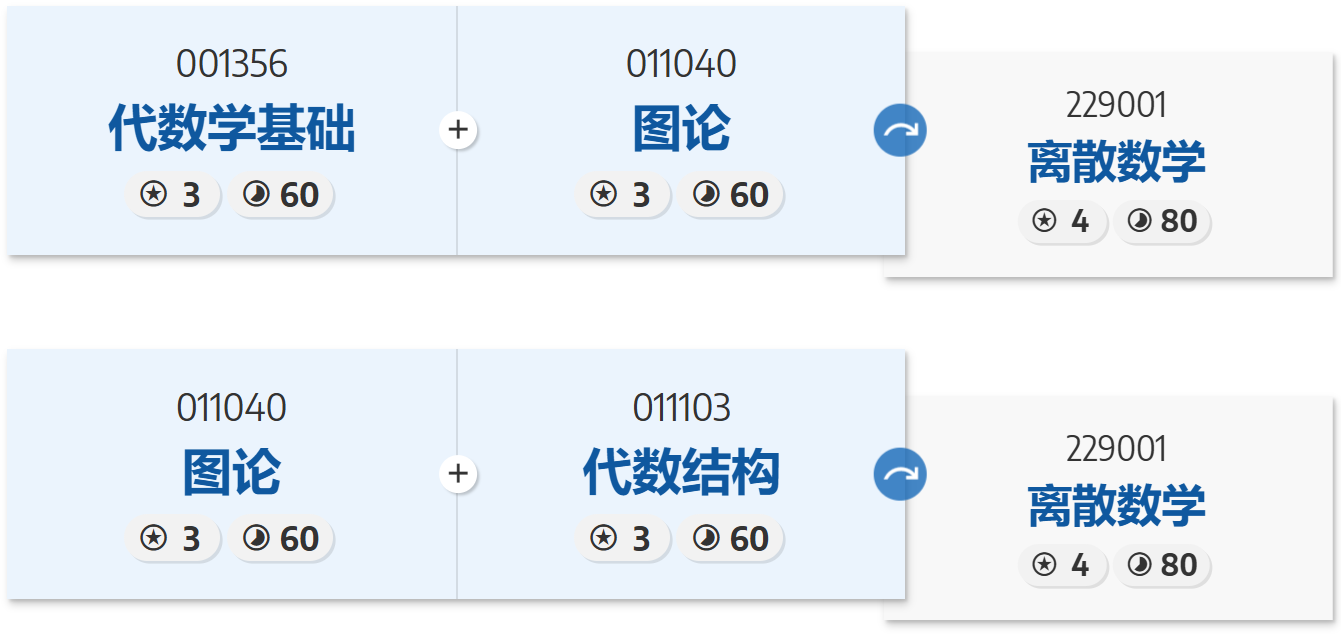
可能用到的替代关系如下图,计科的代数结构开在秋季,数院的代数学基础开在秋季,想深入了解数理逻辑的可以考虑选择计科的数理逻辑基础。(离散数学在秋季开设给 DS,春季开设给 AI,两位老师的课堂风格迥异,大家可以根据自己的喜好自行选择,然后提前一学期修读)
不点名,不小测,老师明确支持我们选择更适合自己的学习方式。一共 7 次作业,每次满分 120 分,总评计算是 作业 : 期末 = 3 : 8(作业超过 100 按 100 计算),期末总分 180,满分按照 \(\mathrm{min}\{卷面最高, 150\}\) 计算,最后继续上调给满优秀率,所以给分相当不错。
2024 秋作业+答案:
作业答案(可能从这些地方找到):
- 代数结构和图论的评课社区;
- 组合数学引论 和 组合数学引论部分习题答案;
- 计科三部曲教材 例题;
- 知乎;
- Ramsey 数下界;
- StackExchange;
- ……
老师的手写讲义(文件太大只能分开上传了):1~5;6~8;9~10。
助教的随堂笔记(文件太大只能分开上传了):1~10;11~18;19~22。
期末试卷(为了方便使用,我敲成了 PDF,顺便敲了一下别的评课里提供的试卷):
- 2024 秋离散数学期末试卷;
- 2023 秋离散数学期中试卷 [来源];
- 2023 秋离散数学期末试卷 [来源](缺失的题目用一道类似的作业题补上了);
本课程和邵老师的研究生课 组合数学 风格较为类似,所以
等也可以作为参考。最后想小声问问邵老师,您说的计算理论和复杂度理论什么时候端给我们本科生作为选修课品尝。猜你想看:少十七(邵老师的知乎)。
2025.1.6
2024 秋 离散数学 期末考试 考试时间:3 小时 总分:180 分
1. (15 分) 对任意整数 \(n\), 求 \(\mathrm{gcd}(24n+4,\ 18n+6)\) 的值并证明. (对 \(n\) 从 \(1\) 到 \(6\) 分别求解可得 5 分)
2. (20 分) 考虑同余方程组 \(x\equiv b_1\ \mathrm{mod}\ m_1\) \(x\equiv b_2\ \mathrm{mod}\ m_2\) \(x\equiv b_3\ \mathrm{mod}\ m_3\) 其中, 对任意 \(i \in \{1,\ 2,\ 3\}\), \(b_i\), \(m_i\in N^*\). 给出该同余方程组有解的充分必要条件并证明. (注意 \(m_1\), \(m_2\), \(m_3\) 两两互素只是有解的充分条件)
3. (20 分) (a) 若群 \(G\) 的阶 \(|G|\) 为素数, 证明 \(G\) 是循环群;
(b) 若群 \(G\) 的阶 \(|G|\) 为 \(pq\), 其中 \(p\) 和 \(q\) 均为素数且 \(p < q\), 证明 \(G\) 至多包含一个 \(q\) 阶子群.
4. (20 分) 设 \(S\) 为 \([m]=\{1,\ 2,\ ...\ ,m\}\) 上的一个置换群, \(F=\{f:[m]\rightarrow \{0,\ 1\}\}\) 为所有 \([m]\) 到 \(\{0,\ 1\}\) 的函数. 对于函数 \(f\), \(g\in F\), 如果存在 \(\sigma \in S\), 使得 \(g=f\circ \sigma\), 则称 \(f\) 与 \(g\) 在 \(S\) 下等价, 记为 \(f\simeq _S g\). 对于 \(f\in F\), 令 \(Z_f =\{\sigma\in S|f=f\circ \sigma\}\).
(a) (6 分) 假设 \(S\) 为 \([m]\) 上的对称群 (即 \(S\) 包含 \([m]\) 上的所有置换), \(f\) 将 \([m]\) 中 \(m_1\) 个元素映为 \(0\), 求此时的 \(|Z_f|\); (对特殊情况 \(m=10\), \(m_1=4\) 求解最多可得 3 分)
(b) (6 分) 令 \(F_o=\{f\in F|f\) 将 \([m]\) 中偶数个元素映为 \(0\}\), \(O_f=\{g\in F_o|g\simeq_Sf\}\). 对于 \(f\in F_o\), 证明 \(|O_f|\cdot |Z_f|=|S|\);
(c) (8 分) 令 \(F_1\) 为 \(F\) 任一非空子集, \(O_f^,=\{g\in F_1|g\simeq_S f\}\). 对于 \(f\in F_1\), \(|O_f^,|\cdot |Z_f|=|S|\) 是否成立? 请证明或给出反例.
5. (15 分) 从 \(3\), \(5\), … , \(299\), \(301\) 共 \(150\) 个奇数中任选 \(n\) 个数, 使得其中一定存在两个数互素, 问 \(n\) 最小可以是多少并证明. (找出最小的 \(n\) 并证明可获得满分, 若你能证明某个更大 \(n<150\) 使得题目要求成立, 可视情况获得部分分数)
6. (15 分) 已知: 对完全图 \(K_{14}\) 的所有边进行红蓝染色, 则一定存在一个红色 \(K_5\) 或者蓝色 \(K_3\).
证明: 对完全图 \(K_{19}\) 的所有边进行红蓝染色, 则一定存在一个红色 \(K_6\) 或者蓝色 \(K_3\).
7. (20 分) 考虑方程 \(x_1+x_2+\ ...\ +x_n=m\), 其中 \(m\), \(n\) 均为偶数且 \(m>n\).
(a) (6 分) 求该方程非负整数解的个数;
(b) (6 分) 求该方程满足 \(x_1=x_2\), \(x_3=x_4\), \(...\) , \(x_{n-1}=x_n\) 的非负整数解的个数;
(c) (8 分) 求该方程满足 \(x_1\), \(x_3\), \(...\) , \(x_{n-1}\) 为非负奇数, \(x_2\), \(x_4\), \(...\) , \(x_n\) 为非负偶数的解的个数.
(b, c 小问对特殊情况 \(n=6\), \(m=16\) 求解每问最多可得一半分)
8. (20 分) \(f\) 和 \(g\) 为定义在非负整数上的函数, 已知对任意 \(n\geq0\) 有 \(\displaystyle{f(n)=\sum_{i=0}^n\tbinom{n}{i}g(i) }\), 证明对任意 \(n\geq0\), \(g(n)\) 可唯一表示为 \(\displaystyle{g(n)=\sum_{i=0}^n(-1)^{n-i}\tbinom{n}{i}f(i) }\).
9. (20 分) 考虑连通有向图 \(D=(V,\ E)\).
(a) 证明若对于任意 \(x\in V\), 都有 \(|\mathrm{deg}_D^+(x)-\mathrm{deg}_D^-(x)|\leq1\), 且任何边 \(a\in E\) 均包含在奇数个有向 \(\mathrm{cycle}\) 中, 则 \(D\) 是 \(\mathrm{Euler}\) 图;
(b) 说明上述命题的逆命题不成立.
10. (15 分) 设图 \(G=(V,\ E)\) 是简单平面图且 \(|V|>2\), 证明 \(|E|\leq3|V|-6\).
2024.12.15
我们需要教材
We need textbooks
教材が必要です
우리는 교재가 필요하다
Nous avons besoin de matériel pédagogique
نحن بحاجة إلى التدريس
Wir brauchen material
Нам нужны учебные материалы
Kita memerlukan bahan pengajaran
Precisamos de materiais didáticos
เราต้องการหนังสือ
Öğretim materyallerine ihtiyacımız var
Necesitamos material didáctico
אנחנו צריכים חומרי לימוד
Χρειαζόμαστε διδακτικό υλικό
Abbiamo bisogno di materiale didattico
हमें पाठ्य-पुस्तकों की ज़रुरत है।
Kita butuh bahan ajar
Avem nevoie de materiale didactice
Имаме нужда от учебни материали
ما به مواد آموزشی نیاز داریم
Potrebni su nam nastavni materijali
Vi behöver läromedel
Tarvitsemme opetusmateriaalia- 课程难度:困难
- 作业多少:中等
- 给分好坏:一般
- 收获大小:没有
- 难度:困难
- 作业:中等
- 给分:一般
- 收获:没有
最大的感受是学的东西多而不精。 拿群论来说,有好多东西作业题里涉及到了但是貌似没讲。比如说有限子群的积还有直积、商群的一些深层次内容。 课程难度很大,而且对于我们这些专业的学生不知道有没有用。(就算有用学了很长时间不用也会忘掉) 这门课是存在问题的,希望教务处或者老师能优化一下这门课。
看完网上的莫比乌斯反演,再看老师讲的,感觉老师讲的比较随意。其实需要挺多前置知识才能学懂、学好、学以致用。 算了不说了,吐槽有什么用呢?
现在我觉得这门课最大的问题是:缺少合适完备的教材,建议搞一本合理的、配套的教材,要不然还是别为难下一届的学弟学妹们了。
话说评课社区就是学生发癫的地方吧…
- 课程难度:困难
- 作业多少:中等
- 给分好坏:一般
- 收获大小:一般
- 难度:困难
- 作业:中等
- 给分:一般
- 收获:一般
期中考试题:
1.对任意整数n,求gcd(21n+4,14n+3)的值并证明
2.若n为正整数,p为素数,证明p不整除n等价于Φ(np)=(p-1)Φ(n) Φ(n)为欧拉函数
3.设G为一个n阶群,证明:
(a)若对于任意d整除n,G中至多只有一个d阶子群,则G为循环群
(b)若G为循环群,则对于任意d整除n,G中恰有Φ(d)个元素的阶为d
4.证明:含幺交换有限环的素理想必为极大理想
5.从1-299的150个奇数中任选n个数,使得其中一定存在两个数满足其中一个整除另一个,求n的最小值并证明
6.考虑方程x1+x2+...+xn=m,其中m,n均为偶数并且m>n:
(a)求该方程非负整数解的个数
(b)满足x1=x2,x3=x4...xn-1=xn的非负整数解的个数
(c)满足x1,x3...xn-1为非负奇数,x2,x4...xn为非负偶数的解的个数
7.二项式系数的题,不好敲字,总之是Cni这种
8.蚂蚁爬,每次向上,向下,向右走1,经过m步走到点(k,k)
(a)证明m是偶数
(b)求一共有多少种走法
(c)上述走法中不跨越直线y=x的走法有多少种
仅供以后选此课程的同学参考
期末反正我应该是不会整理了,考完就结束了😋😋😋
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:很多
这门课没有像样的教材也没有ppt和老师的讲稿,自学起来似乎有一点点困难…
内容方面:主要讲了数论与群论的基础内容(大概与代数学基础相当,但是代基讲的更多一些),组合计数(个人觉得课程很精彩的一部分是组合计数和前面的群论联动的部分),以及图论(美中不足的是这学期老师事情比较多,这部分的内容讲的就比较少了)。
老师的板书有点杂乱,开个小差回来就不知道讲到哪了(悲。不过老师讲课思路非常有意思,当你全部听懂的时候会感觉讲的很好,但是如果没听懂就是另一个故事了。本学期的助教建了一个网站,可以在网站上查看助教的笔记自学,还是非常不错的
作业有点小困难,不过由于作业总分溢出所以混混平时分还是很轻松的。
希望老师下次能做个ppt或者给出latex讲义/ll
容错率很高的考试!按3:8比例计算总评的情况下4.3率可能能达到接近20%(而且似乎还要继续调),神!
- 课程难度:困难
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:很少
- 给分:超好
- 收获:很多
明天期中考试,先来占个坑
邵老师上课还是很nice的,比较循循善诱,对于一些定理会讲动机,让大家一起算。上课比较有参与感。离散数学的内容比较离散,所以邵老师说他力图用一些问题将内容串起来。比如计算欧拉函数,期中之前讲了数论的方法,期中之后又讲了组合的方法(容斥原理)。对于一些深刻的定理或思想,邵老师会避免陈述定理最一般的形式,而仅仅给出基本的例子。比如莫比乌斯反演,只讲了集合和数论的版本,又比如Polya计数原理,只讲了对n边形用m种颜色染色的例子,还用莫比乌斯反演给出了另一种解法。我认为这是好的,保证了课程深度的同时又不要求大家有很多数学基础,还在大家心中埋下了一颗科学的种子?邵老师的意思是离散数学是一门导论课,可以把大家导到近世代数,组合学和图论上去。总之这学期上课还是比较有收获的,但我建议邵老师把字练一下,把板书写好看一点,或者以后有时间可以整理一个latex讲义。
期末考完了。。。邵老师说期末会比期中简单,大概40%的同学会考85分以上。奈何本人水平太差,愧对老师教诲,只会做80分不到的题。下面是期末考试回忆版:
1.已知对K18染色或者存在红色K5,或者同时存在红色K4和蓝色K3.证明对K35染色一定存在红色K5或蓝色K4.
2.(a)图同构等价于关联矩阵置换相抵(b)关联矩阵置换相抵于分块对角等价于图不连通(c)证明关联矩阵的秩小于等于顶点数减去连通分支的个数
3.(a)简单连通图有一个圈等价于|V|=|E|.(b)若|V|-|E|=k,图中存在两个顶点之间有k+1条路径
4.证明连通简单平面图有一个顶点度数小于等于5.
5.(a)n对夫妻排成一行,求每对夫妻不相邻的排法(b)n对夫妻排成一行,求每对夫妻不相邻,且同性不相邻的排法。
6.对正方形用n中颜色染色。(a)用了至多三种颜色的染色数(b)排除旋转、对称下重复的染色方案求方案数(c)排除中心对称和绕对角线翻转下重复的方案,求方案数(d)在(c)的基础上求至多用了三种颜色的染色数。
7.S为n元集合,f,g是定义在S的子集上的整值函数。已知对于S的偶数元子集,有f(X)=\sum\limits_{Y\subseteqX, |Y| is even}g(Y), 对S的奇数元子集,有f(X)=\sum\limits_{Y\subseteqX, |Y| is even}-g(Y).问题:对于S的奇数元子集X,计算\sum\limits_{Y\subseteq X}f(Y).
几乎没有送分题,建议后来者把老师的讲义全部看懂,这样考试应该能做出大多数题。本人觉得menage问题太难应该不会考,结果就考了还有24分,o( ̄ヘ ̄o#)(主要是邵老师说期末会比较简单)。
PS:期末卷子里最有意思的一道题应该就是第二题的(c)问了。考场上有了思路没做出来,刚刚吃完饭想出来了。首先,前两问的铺垫告诉我们只要对连通图证明rank小于等于顶点数减1(此题的关联矩阵是对于有向图而言的,这里连通的意思是有向图生成的无向图是连通的)。如果图中包含cycle,将cycle上的边在关联矩阵中对应的列进行线性组合会得到0(规定一个定向,正向边加上该列,反向边减去该列),此时关联矩阵不满秩,rank小于等于行数减1等于顶点数减1.所以我们只要对连通的无圈图(也即树)证明结论即可。这是显然的,因为rank小于等于列数等于边数等于顶点数减1.
这题比较的代数,也比较图论。下学期数院开代数图论,感兴趣的同学也许可以选一下?
- 课程难度:困难
- 作业多少:很多
- 给分好坏:超好
- 收获大小:一般
- 难度:困难
- 作业:很多
- 给分:超好
- 收获:一般
btw,如果你是大一搜索离散数学看到了这个评论,那么说明你大概率在研究DS培养方案考虑转专业问题,鄙人在专业选择上有一段波折的经历,由此写了一些关于妮可新工科专业的信息分享,感兴趣可以在 https://github.com/yueyue0407/some-ideas-about-switching-majors-in-USTC 查看,希望能帮助到你QAQ
5.25 update 大二下都要结束了才来评论而且人已经不在DS了QAQ
回首在DS学习的一个学期,邵邵的课无疑是最令人愉快的课程之一。
先来说课程本身,Discrete Math 这课是完全的 discrete ,内容包括但不限于 集合逻辑、数论、组合计数、群论、图论… 任何一个部分都能单拎出来作为一个大课来上。然鹅DS天才地将所有的这些压缩到一门4学分的课程里面(隔壁CS好歹也是 代数结构加 图论 两门课好吧),导致这门课实际上造成了老师和同学的双重折磨,既考验老师的功底和讲课水平,又挑战学生的理解能力… 因此,这门课就像婺源的量子力学一样,不同的老师有迥异的风味。
邵邵也是意识到了这个问题,教学时略去了中学学过的集合逻辑部分,期中考试前讲授数论组合和部分群论内容,下半学期着重于图论并把群论补全。邵邵作为妮可首届华罗庚班班长加海归,功底非常深,上课跟着他的节奏学习会让你感觉如沐春风,然后回去自己做就一脸懵壁了😭。建议上课时一定要自己记笔记,邵邵虽然会发他的笔记,但是那个字迹实在是…而且还是上课的原版,有些随堂的灵感内容如果不结合课堂实况是很难找到逻辑的(因为他们往往会出现在笔记的犄角旮旯…)。作业的难度较大,需要长时间的思考和查询资料,而考试大多数题目则是例子和作业的变体,较为友好。给分很大方。助教也很负责,每次习题课都能把作业讲清楚,感觉他们在这个课上花的时间比我这个学生多得多 ε=ε=ε=┏(゜ロ゜;)┛
邵邵作为过来人,也会分享一些他的感悟和经历,他疫情下出国的故事实在是给了我很大的触动。
最后,感谢邵邵,也祝愿邵邵的家人早日康复!
想复习无从下手,红了😭😭
- 课程难度:困难
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:中等
- 给分:超好
- 收获:很多
本身计算总评只有2.0一打开成绩单3.0不多说了邵老师再生父母
从今以后我不允许任何人忤逆邵老师
感谢的话说完了,现在来认真的评价一下这门课吧。
- 感觉比较难受的是没有一本系统性的教材或者讲义,导致每次上课都有一种开盲盒的感觉。虽然课程主页有大纲但还是上的比较茫然和吃力。
- 老师讲课的水平毋庸置疑,非常善于启发学生的思考,逻辑清晰,有深度有广度,讲的内容都非常有水平,一节课的高度集中注意力结束后会有很通畅通透舒适的感觉,总之就课堂体验来说绝对是可以称之为艺术品的课堂。
- 奈何本人对于抽象数学的天赋实在有限,150分的卷子只写了70分。以及作为aids的班,班上真的很卷,出来一些少院大佬,希望后来的学弟学妹们不要相信一些佬们所说的期末考试内容不算难,认真听课写作业就能得高分诸如此类的话!
- 作业是有难度的,至少我没有几道题是能够靠自己的思考完全写出来的,期末考更是破防加破防,在临近考试时复习真的非常崩溃。没有办法把握住系统性的重点,也没有熟悉到能够举一反三解决同类问题。总会给人一种见一题不会一题的感觉🤣,所以那些觉得不难或者认真学就能学好的别轻易相信。至少我知道我是付出了150%的努力了(或许确实没什么天分)但这门课就是很有难度不是能让人通过认真学习认真上课就能得到优秀的(没有打击后来者的意思,纯纯个人看法)老师非常有胸怀和视野,在课程结束后甚至给每位同学都发了邮件写下了老师对于这门课的想法和对于学生的祝福,非常的温暖,在科大为数不多的感受到老师对于学生的人文关怀。
- 同时我的想法是不需要因为自己缺乏这一方面的天分就觉得压力山大,因为每个人的天赋点不同,东边不亮西边亮。(这是本人这学期结束后的深刻体验)
- 来了大数据后就不要有什么心怀侥幸了,身边的同学大概是除了少院最卷的一批了,所以或许有时候真的得学会和自己比,因为和别人比永远有比不过的时候。在科大无论再难的题都有人觉得简单。离散数学这门课能认识邵老师让我觉得很幸运,只是过于离散数学和我并不投缘,但希望后来者可以窥探到学习之美,正如邵老师所说!
- 课程难度:中等
- 作业多少:中等
- 给分好坏:一般
- 收获大小:一般
- 难度:中等
- 作业:中等
- 给分:一般
- 收获:一般
课程定位似乎有些问题,计科有离散三部曲,而aids居然用一门课就涵盖了这三门课。
老师水平确实很高,没有照着课本的思路,而是先从抽屉原理引入,显然是对如何上好这门课有着自己的思考。但是只上了一节课,所以暂时不多评价。
除了上课内容本身之外,这门课的其他地方也让我眼前一亮。
1.老师不要求到课,说“只要同学们觉得自学比上课好,那就可以不来上课。”
2.有课程主页,给出了作业/参考书/教学安排等重要信息
3.给分标准改革。作业/考试会有120分,只需要得到100分就会拿满该项;平时:期中:期末=3:4:4,留出了一定的冗余。
“经常有同学说总评100分难拿,你上我的课,肯定很容易拿100”
第一节课老师上课迟到,扣1分。但由于总分11,留出了1分冗余,所以总评为10分。
(吐槽一下,那个教室真的热
- 课程难度:困难
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:很少
- 给分:超好
- 收获:很多
这个离散越复习越发现啥也不会啊,我怎么去考试啊,
怎么办怎么办,电磁甚至一点没学,后面的考试都没学,能活吗
what can i say man
现在是深夜一点,距离离散考试还有七个小时
会活吗
邵老师,邵老师,我明年还会来的!
- 课程难度:简单
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:简单
- 作业:很少
- 给分:超好
- 收获:很多
要期末了感觉啥也不会,最近还有较频繁的作业,好焦虑啊˃ʍ˂
演都不演了😭出题要有挑战性是吧,我不活了😭
- 课程难度:中等
- 作业多少:中等
- 给分好坏:一般
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:一般
- 收获:很多
邵老师开的离散数学课程与科大别的离散数学课程在内容上会有很大的不同,也因此没有一本教材可以囊括本课程所有的内容,需要大家上课认真听/多找一些资料参考。
由于邵老师同时教研究生课程《组合数学》,所以这门课和组合数学有相当一部分是重叠的。首先提醒大家,邵老师所讲的所有与组合、计数相关的内容均可以在《组合数学引论》中找到相关的例题和习题。
课程开篇讲述抽屉原理,然后用抽屉原理推出中国剩余定理解的存在性,进而过渡到数论模块。
数论模块介绍了裴蜀定理、同余、欧拉函数等内容,在讲到唯一分解定理的时候引入了环的概念,介绍了素元和不可约元,为后续讲代数结构做铺垫。数论的最后介绍了 RSA 加密算法(似乎邵老师在 23 春的算法基础课程里也讲了这个)。
代数结构部分的重心是群和环,域基本没怎么讲。群的部分的重点是陪集分解的一套理论以及群同构,还介绍了循环群、置换群的部分内容;环的部分的重点是素理想、极大理想、素元、不可约元之间的互相推导及依赖条件,这是课程的一个小高潮部分。
随后开始的内容是组合计数,这在大多离散数学的课程里是不会花大篇幅去介绍的。这一部分以给项链染色的问题引出了莫比乌斯反演和 Polya 定理两种思路,然后从组合计数最基础的定理、不定方程解的个数等问题出发讲了若干组合恒等式的内容。在不定方程解问题的最后引出了容斥原理(请重点关注错排问题和 ménage 问题),进而介绍了子集反演(邵老师直接称之为莫比乌斯反演)、数论的莫比乌斯反演等内容。这中间又完整介绍了群论里没细讲的群作用与轨道公式,用莫比乌斯反演和 Polya 定理两种方式解决了最初的项链染色问题。
最后一部分是图论。本学期由于时间关系,图论的内容讲的很少。开篇是欧拉回路问题,进而介绍了图的基本概念以及连通性相关问题。然后单独讲了一个 Ramsey 问题(这个是必考的内容,请后来者注意),这是抽屉原理与图论的结合。最后又讲了树的概念和平面图的概念,证明了平面图的欧拉定理。
如果时间充足的话,应该还会讲解图论中与矩阵相关的知识、割问题这些非常经典的内容。
而完整的离散数学还应当包括数理逻辑的内容,只是邵老师将其略去了。数理逻辑的内容非常深刻,比大家在中学时代所接触的命题等内容要深刻得多。计科以前用了 3 学分才能讲完完整的包括 Gödel 不完备定理在内的数理逻辑知识,所以这门课讲不了那么多也可以理解(真要讲的话可能大家连语法和语义的区别都还没弄清楚就结课了)。
本学期因为种种因素没有期中考试,期末考试的题目别的评课已经回忆了。今年的期末卷子难度不大,把基础分都拿到基本就稳稳 4.3 了,因为算分公式比较暴力(平时:期末=3:8,期末按 100 * 总分 / min(150,最高分) 算)甚至总评 100 分也不算难。
总的来说,这是一门很硬的课程,即使是在如此暴力的算分公式下,如果不调分优秀率也才 30%。希望后来者能在这门课上多花一些心思。这门课的助教都很厉害,提供了很丰富的学习资料,给了大家很大的帮助。希望后来者能喜欢这门课。
出分了,跟预料中一样的三位数总评,感恩😊
- 课程难度:困难
- 作业多少:中等
- 给分好坏:一般
- 收获大小:很多
- 难度:困难
- 作业:中等
- 给分:一般
- 收获:很多
2.3
终于出分了,给分大概还是参考3:4:4,算出来也和预期的差不多,这学期唯一的4.3,我认为还是很不错的
1.17
预估分应该不会这么快出了,先来评价一下,这门课平时,期中,期末占比是3 4 4,加起来是11,同时期中期末最高是120分,考到多少分按多少分算,所以你算总评最高可以达到126分
整门课程的内容大概分为
抽屉原理->数论->群论->组合->图论
组合大抵可以分为组合计数,容斥原理和Mobinus反演
图论内容可以参考徐俊明的《图论及其应用》第四版
再贴一个我自己写的期中之前的内容(有些内容不一定完全正确,可以当提纲参考)
不过我感觉这门课确实存在问题,很多的内容塞在这个四学分里面,导致正常上的话是上不完的,所以这学期的课程都比较具有跳跃性,再分一门课出去应该会比较好
再谈一下选课,ds人必修逃不掉,不过从计科转来ds的可以尝试修图论来替代掉这门课,别的院的建议就不要选了,这门课真心不轻松
先占个坑,不知道期中考试会有多难
11.26
诶,复习的有点破防,虽然是离散数学,但为免有点过于“离散”了
11.29
期中考完,客观评价一下,本张试卷容错率还是蛮大的,120的满分,再加上一半的计算具体值的分数,比我预想的要好很多,试卷上的题目大多也是平常作业或者上课讲的题的变式,除了第四道(?)和最后一道,其他的难度都不算大。
- 课程难度:困难
- 作业多少:中等
- 给分好坏:一般
- 收获大小:一般
- 难度:困难
- 作业:中等
- 给分:一般
- 收获:一般
老师简直是大学以来听过思路逻辑包括讲课技巧什么的最顶的老师了!唯一一门能从头听到尾的课(虽然真的是对我太难太难太难了,应该是我太辣鸡了)虽然没学明白,作业考试都不太会,但老师讲的确实很好啊。
课程对没基础的我来说真的顶天难了😭😭😭
等待捞分,其他待出分再说
啥也不说了上图

- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:很多
显然,注意到,结论平凡
易得,答案略,留作习题
同理,不妨设,由上可知
证毕,QED,自证不难
- 课程难度:困难
- 作业多少:中等
- 给分好坏:一般
- 收获大小:很多
- 难度:困难
- 作业:中等
- 给分:一般
- 收获:很多
离散要把我g爆了 给分未知 等一手吧 2.3出分 不多说了。感谢ss
- 课程难度:困难
- 作业多少:中等
- 给分好坏:一般
- 收获大小:很多
- 难度:困难
- 作业:中等
- 给分:一般
- 收获:很多
老师讲课很好,但是感觉现在期末无从下手,知识点太多了……
周围同学都认为很简单,而我觉得要爆炸了,希望助教改卷大放水
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:很多
ss老师谁不爱呢?
十分
wt can I say?
(注:这是我到科大之后第一次认真听课 没办法,老师讲的实在是太好了,让我恍惚间找回了曾经热爱数学的自己……)
老师真的太好了😭😭😭
180分卷子 还有3比8的算分方式 躺下等捞就好了😍
- 课程难度:困难
- 作业多少:中等
- 给分好坏:一般
- 收获大小:很多
- 难度:困难
- 作业:中等
- 给分:一般
- 收获:很多
今天考完了,考场上突然发现区区十题题目难写起来还真难写呢,什么都不会写的题目比如代数结构的好歹也写了一点吧。这门课没有基础的话应该是比较难,比较难是应该的。我个人上课基本上听一半就关机了,跟同学聊天讨论这些问题虽然不知道费尽心思证明是为了什么,但是我知道我真的是费尽了心思。
- 课程难度:困难
- 作业多少:很多
- 给分好坏:一般
- 收获大小:很多
- 难度:困难
- 作业:很多
- 给分:一般
- 收获:很多
后天期末考试,今天来写点评价。
这门课难度很大。包含了很多内容但是受限于一门课的体量没有办法深入介绍,这一点其它评论也有提到。
授课方面相当出色。邵帅老师会把证明过程以非常有逻辑且合理的方式一环扣一环地呈现给同学,手把手教同学如何处理问题。在听完之后不会有任何形如“为什么要这么做”的问题,而是会觉得“这个问题从直觉上来说就应该这么做”。之后再去看参考书上的证明就会觉得与课上的证明有明显差距,只是把某件事情证明出来而并不告诉你其中的道理(这种感觉很像读一些国内教材与国外教材的差距)。
接近学期末的时候邵老师跟我们说到成绩的问题,他觉得成绩并没有那么重要(也是老生常谈了),并且说了一些个人经历作为佐证。这一点我非常认同。所以18周周末的加课,虽然处于考试周并且上课内容不在考试范围内,我还是去听了。
最后一节课(也就是那节加课)结束的时候,邵老师对在场的大约10位同学说“希望今天来了的同学都能拿4.3”。考虑到不太好看的期中成绩(上半学期由于诸多事务,课程没太跟上)和并不出色的作业成绩,这句话对我来说绝无可能。但是我确实认同老师所说的,学到一些数学思想,并且在今后的人生中能够产生一点影响,比成绩重要的多。所以就算最后只拿到2.0甚至更低的绩点也无所谓了。
1.11更新
上午考完了期末,可以说尽力了。组合部分考了Menage问题,有些难度,第一问大概率没算对,第二问只写了n=3的情况。图论部分的证明有些也没做出来。
2.4更新
出分了,确实很差(笑)
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:很多
这门课在期中前主要学习数论 群论 抽屉 组合 容斥,知识点很离散。不过考试题基本是作业原题,稍微有点变化,难度并不大。作业也比较少,还是可以快乐的水完这门课的 马上要期末了 考完试来评价一下0
期末好难 下一届学弟学妹一定要学好组合学 出分了 4.3 也算在意料之中吧 总评应该是按344给的
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:很多
邵帅老师超级可爱!而且现在两周一次作业平摊下来作业量也不大,主要是邵老师上课会讲非常多的思路,上课比较轻松,很有意思!
成绩上344给分,期中期末满分都是120,总评满分126,有不小的冗余空间,对于冲100的同学很有优势。
核院老狗并没有学过相关的数学知识,但是只看老师的讲义也做出了大部分的考试题,私以为考试难度其实并不是很大。
虽然这学期的体验不错,但是课程内容上的设计不是很赞成。邵老师似乎是想把离散数学按照导论的形式讲,通过浅或者娱乐的形式介绍其中的各种内容,但是这样对于大二或者大三的学生而言是很少有机会去深入学习其延申知识的。同时由于时间安排问题,相当重要的数理逻辑部分被一笔带过,这是非常可惜的一点。私以为可以像丁虎老师一样加入一些计算机数学的内容,同时舍弃部分过于数学的内容和一些深度,让课程更加贴近计算机和大数据,在开在大二的现在当作导论讲解并不是很合理的。
- 课程难度:中等
- 作业多少:中等
- 给分好坏:一般
- 收获大小:一般
- 难度:中等
- 作业:中等
- 给分:一般
- 收获:一般
为什么期末不给查分😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡
- 课程难度:困难
- 作业多少:中等
- 给分好坏:杀手
- 收获大小:一般
- 难度:困难
- 作业:中等
- 给分:杀手
- 收获:一般
能跑就跑,没学过数竟的ds人最好大一春就提前修,来这里纯粹是精神折磨+被摁在地上摩擦+收获低绩点,别信评课社区蹦的大佬
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:很多
本人是听课党,学之前几乎零基础,除了听邵老师讲课外没看其他资料/网课,也没做作业以外的其他题目,出分后按照给分公式算出来总评甚至超过了100(?
建议没有修过相关课程或者没有数竞基础的同学认真听课(强烈建议不要翘课,因为本课程知识的连贯性挺强的,少一次课可能会导致后面的课听不懂),上课的时候尽量跟上老师思路(跟不上也没关系,我听课的时候也经常慢半拍,但一定要动脑子思考),老师提出来的一些问题可以积极回答(不过我回答了几次都是错的hhhh),边想边把老师上课写下的板书记下来(因为本课程没有教材,没有讲义(虽然助教会写一份以及课程最后老师会把之前的讲义发出来,但自己写下来能加深印象),记下来的笔记可以方便复习(做作业的时候不会可以翻一翻,作业很多题老师上课都有提及,有些提示啥的))。考试挺轻松的,至少比作业题简单,基本都是基础题,有几道题甚至考前的习题课刚讲过类似的。
考试实在不会做可以试试枚举,反证,数归……把能推出来的结论都写上去,会给不少分的。
总结:老师上课有意思,认真听课收获很大,给分很好,强烈推荐!
- 课程难度:困难
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:中等
- 给分:超好
- 收获:很多
教课水平超神,学不会是我的问题。但是没有教材真的太伤了,加上期中因为老师有事没考,期末真的无从下手o(╥﹏╥)o 靠老师和助教发力了