2020春 课程号:00166501
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
| 选课类别:计划内与自由选修 | 教学类型:理论课 |
| 课程类别:本科计划内课程 | 开课单位:数学科学学院 |
| 课程层次:专业基础 | 学分:4.0 |
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:很多
开吹了,开吹了,非风洞工作人员请离开!
殷老师和陈老师一如既往尽职地讲了一学期好课.
在开学前讲了两节课内容的多变量微分学,罗列定义定理与一些基本方法点,主要是为了电磁学A课程的学习稍事铺垫,学期最后又用了两节课讲完了多变量积分学,讲了一些微分形式和雅不堪的Stokes公式.
从一般拓扑学(或者叫点集拓扑学)开始讲,把妮可对应的拓扑学(H)的点拓部分基本讲完了,而且有诸如Ascoli-Arzela定理,Stone-Weierstraβ定理等有点泛函味道的定理;这部分同时穿插了赋范向量空间.(大二开始终于体现了中法班课程设置的宏观性和总体性,线性空间知识在代数I就讲完了所以分析II就可以直接使用,分析II一开头就讲了点拓,代数II后期研究诸如特殊线性群,特殊正交群,辛群的时候拓扑的概念也可以直接拿来用.)在这一部分讲完之后就是函数项级数与幂级数,里面已经讲到了一些复分析的小结论了,比如Cauchy积分公式,平均值性质,最大值性质,唯一性定理等,这一部分成功地把所谓一致收敛/内闭一致收敛讲得非常透彻.这一部分的一个自然承接就是ODE理论,构造一列函数去一致逼近初值问题的解,还有比如利用Wronsky行列式找别的解等等.法文课本MPSI最后一部分就是广义积分,当然这就是一个积分+一个极限,处理的时候想着这是个极限就行了.后面补充了Riemann积分的一些理论,数学分析A1学的内容,然后是含参积分的一大套理论,包括比较复杂的含参广义积分和各种交换次序问题.最后一周讲了两个大习题,一个是Pólya定理,一个是关于判定无理数的小东西.这里放一下第一个定理的内容
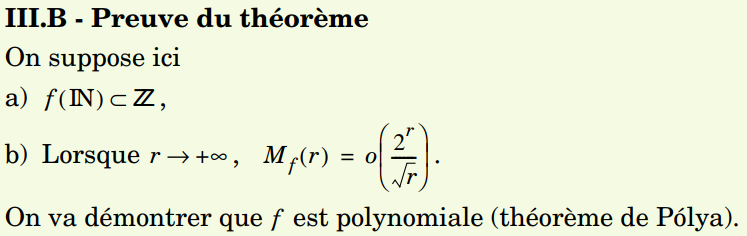
(这个世界杀死了我这种不会法语的人.docx)
正课主要是这些内容,习题课也很雅.首先整体上是跟着正课的进程去找习题和讲习题的,第一节课因为正课还什么都没讲的时候给我们科普了一下他工作的领域一些工作和我们都能理解的小结论,并且用最优传输证了下等周不等式.最后的时候也是介绍了不少很新很有趣的结果,比如十几年前的有限域上的Kakeya猜想的非常初等的证明,还有一些方程和凸分析的小东西,非常有趣.这学期由于疫情的影响,只进行了一次口试,是我最后一次见到陈老师(雾)
学生助教是吴天学长,工作尽职尽责,也会开习题课讲作业,热心向同学们讲解.
给分也是好不堪,当然,你选了这个课一般都是置课,而且也没法换,就不多说了.
总之是受益匪浅,yyds!!!