2025秋 2024秋 2023秋 课程号:MATH200302
-
少年班学院
- 少年班学院培养方案(数学与应用数学)
- 少年班学院培养方案(信息与计算科学)
- 少年班学院培养方案(物理学)
- 少年班学院培养方案(高分子材料与工程)
- 少年班学院培养方案(化学)
- 少年班学院培养方案(地球物理学)
- 少年班学院培养方案(大气科学)
- 少年班学院培养方案(机械设计制造及其自动化)
- 少年班学院培养方案(通信工程)
- 少年班学院培养方案(网络与新媒体)
- 少年班学院培养方案(数据科学与大数据技术)
- 少年班学院培养方案(环境科学与工程)
- 少年班学院培养方案(生物技术)
- 少年班学院培养方案(量子信息科学)
- 少年班学院培养方案(应用物理学)
- 少年班学院培养方案(天文学)
- 少年班学院培养方案(安全工程)
- 少年班学院培养方案(电子信息工程)
- 少年班学院培养方案(电子科学与技术)
- 少年班学院培养方案(信息安全)
- 少年班学院培养方案(光电信息科学与工程)
- 少年班学院培养方案(理论与应用力学)
- 少年班学院培养方案(能源与动力工程)
- 少年班学院培养方案(自动化)
- 少年班学院培养方案(核工程与核技术)
- 少年班学院培养方案(应用物理学-核)
- 少年班学院培养方案(计算机科学与技术)
- 少年班学院培养方案(地球化学)
- 少年班学院培养方案(人工智能)
- 少年班学院培养方案(工程物理)
- 少年班学院培养方案(空间科学与技术)
- 少年班学院培养方案(测控技术与仪器)
- 少年班学院培养方案(生物科学)
- 少年班学院培养方案(工商管理)
- 少年班学院培养方案(管理科学)
- 少年班学院培养方案(统计学)
- 少年班学院培养方案(金融学)
- 少年班学院培养方案(材料物理)
- 少年班学院培养方案(材料化学)
- 少年班学院培养方案(网络空间安全)
- 少年班学院培养方案(行星科学)
- 少年班学院培养方案(集成电路与集成系统)
- 少年班学院培养方案(大数据管理与应用)
- 少年班学院培养方案(机器人工程)
- 数学科学学院
- 人工智能与数据科学学院
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
| 选课类别:计划内与自由选修 | 教学类型:理论课 |
| 课程类别:本科计划内课程 | 开课单位:数学科学学院 |
| 课程层次:专业基础 | 学分:2.0 |
教学水平与课程内容
申屠钧超老师被普遍评价为一位优秀的教师,其课堂风趣幽默,善于引导学生思考复杂的几何概念。课程内容涵盖广泛,从古典几何的历史入手,逐步深入到现代几何及其背后的代数工具。课堂上不仅仅局限于教材,还会拓展许多内容,丰富学生的视野。不过,因为课程内容可能涉及较多的线性代数知识,部分同学建议最好有一定的线代基础后再选这门课程。
考试与作业
课程的考试包括期中和期末,整体难度适中,不过部分题目可能需要扎实的线代功底。作业量相对较轻,两周交一次,习题课提供了有价值的补充材料,助教认真负责。针对作业的反馈为“即使难度不高,但需要严谨地书写过程”。
给分与课程政策
给分普遍被认为是“奶”,许多同学提到最终成绩得到了申屠老师的“关照”,即使考试分数不高也能拿到较高绩点。不过此前曾有关于期中、期末考试分数差距较大时存在的“进步奖”的政策引发争议,目前该政策已取消。据反馈,申屠老师在查卷和最终评分时显示出了很大的宽容和帮助性。
学生反馈
普遍反馈显示申屠老师受学生欢迎,多数同学认为值得毫不犹豫选择这门课。老师的教学方法和课程设计被不少同学称赞为激发了对几何和数学的兴趣,并为后续课程的学习打下了基础。也有意见认为课程的设置应该在完成线性代数的学习后进行,以便学生更好地理解其中涉及的代数内容。
总结
《几何学基础》课程在申屠老师的授课下显得生动且富有深度,虽然有些内容需要线性代数的铺垫,但整体来说是一门值得推荐的课程。通过课堂学习,不仅获取了几何学的基础知识,还培养了深入思考的能力,是一次充实且富有挑战性的学术旅程。各类反馈几乎一致推荐选择申屠老师的课程,并强调了他对学生的支持和帮助。
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:很多
老师讲课很好,表达很清楚,风格风趣幽默,确实可以学到不少东西😋给分比较不错,两次考试都是联考,整体难度不算大,压轴个人感觉具有一定难度,最后87+93爆了4.0(大概率是卡绩了。。) 卡绩显然是自己的问题,怨不得别人。 但是扣的这一分(实在是非常抱歉,如果日后进一步了解可能会补上)主要是因为今年一个很奇怪的政策,期中期末进步二十分以上会有额外加分,而这个加分力度之大可以说令人发指,以至于可以达到期中多漏一道题反而能上4.3的逆天程度,实在是无法理解。 还是非常推荐申屠老师,可以无脑选
——————
二编 刚刚得知本身总评分数高低居然有用🤣
但由于zjgg疏忽期中查卷分数没有加上 老师竟然以没有改变任何人绩点为由拒绝修改总评 导致本人折算总评94→92,感觉是令人汗颜😅遂修改至6分
2.1再次更新
最新消息显示st已取消幽默鬼晦进步奖😆及时改正值得赞扬 遂上调此一分)
分割线
最新奇观之神秘助教莫名其妙辟谣本条绝对真实消息并动用权力大搞一言堂,下面附有完全真实连贯聊天记录,间断是因为达到截屏高度上限,如果有半条裁切我也可以直接从二号楼顶楼跳下去(反正这是完全不可能的)


感觉其对pksq的评论也神秘至极,还留待各位评价吧,算见识到无形大手的威力了)
不过鉴于其神秘行为和老师毫无关系,降低评分显然毫无道理,还是把分数保持不变为好)
- 课程难度:中等
- 作业多少:很多
- 给分好坏:一般
- 收获大小:一般
- 难度:中等
- 作业:很多
- 给分:一般
- 收获:一般
2025 秋助教。
这门课的领导权实际在🚀老师手中,因此其任务量极大(私以为对应 2 学分的课程是完全不合适的)。课程的作业量较大(本人改的两周作业共 25 小题,120 个人就是 3000 小题,其中甚至包括大量几何证明,当时差不多改吐血了,改了三周才改完),而且有两次计入总评的小测(占比 10%)。虽然小测🚀会提前透题(小测就改个数字),这对于本就很忙的大一同学应该造成了不小的压力。期末考试本人因为恰好有两门连着的考试既没监考又没改卷,但考完看了看感觉难度实在太大了,只能说我做这卷子未必能上 90。课程最后给分应该是由🚀老师决定,不过罗助教已经把大家的平时分捞到极致了。
期末分布
| 平均 | 63.14 | |
| 中位 | 66 | |
| < 60 | 45 | 36.89% |
| >= 60 | 77 | 63.11% |
| >= 70 | 44 | 36.07% |
| >= 80 | 13 | 10.66% |
| >= 90 | 5 | 4.10% |
| 总人数 | 122 |
这种分布直接导致了无论怎么调分 4.0 以上的占比都无法超过 15 %(助教已经尝试过各种调分方法了)
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:很多
24助教占坑,评论应该会跟随课程进度更新。
几何学基础这门课是大家在大学接触的第一门“几何”课。不同于其它学校所开设的第一门几何课程,几何学基础这门课绝不拘泥于“解析几何”这一范围,而是从历史的角度出发,逐步介绍古典几何学中的经典内容。其中,我们将初窥“线性代数”的影子,其是在处理这些几何问题中的第一类重要工具,利用之我们可以证明几个漂亮的分类定理。有了这学期课程的铺垫,大家后续理解线性代数中的一些概念会更加自然。(所以我之前把这门课戏称为“线性代数A0”)
申屠老师是非常好的老师,上课风趣,介绍的内容很广泛也很有深度,在其课上只要认真听讲了,基本可以在愉快的氛围中学习到许多知识。作为助教,我会在习题课上补充介绍一点老师上课提及的拓展内容,或者补充一点必要的线性代数知识,或许还会夹带一些私货。
这门课看似是大家在大一上最轻松的一门课,不过想拿好成绩还是需要下功夫的。现行的讲义有许多课后习题,作为初学者建议有时间的话把习题都做一做。后续学习几何学的经验告诉我,学几何一定不能怕“算”,几何学基础里面也涉及了一些基础的计算,这不仅是学习中的重点,也是考试拿分的关键。
课程群号:314428468,祝愿我们度过愉快而充实的一个学期!
- 课程难度:简单
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:简单
- 作业:很少
- 给分:超好
- 收获:很多
绝对值得选!!!
再加上申屠老师好帅,加一分,总共给11分。
据说申屠老师是pksq好评榜排名第八的老师,绝对实至名归!
今日(12.24)结课了,遂来水点评。
首先呈上两张课堂精彩瞬间:

前四节课讲数学史,从古希腊数学的起源一直讲到了20世纪的现代几何学,给人一种“you can't help but awe”的感觉,大气恢弘弄而又极其深刻。按照老师的原话说,这四节课的目的是为了“震碎我们的三观”。

第五节课才开始进入正题,介绍内积、范数、度量等概念,但他一直避免提及“n维欧式空间 R^n”,而是尝试让我们在线性空间(V)的意义下理解这些概念。直到第八节课,老师讲到外积了,才不得不“从空中降下来,回到地球(也就是三维欧式空间R^3)上”(申屠老师原话,当时我差点笑了出来)。
在这段时间,申屠老师上课非常喜欢拓展内容(吹水),感觉平均下来前几节课有¼在拓展内容(吹水)。要是没有《几何学基础》的教材限制,他可以给你拓展三本《几何学基础》的内容。在课堂上拓展了完了不算,还要课下在群里发文件继续给我们拓展。以下是发到群里的若干文件中的其中三个,供大家参考参考:
数学分析原理【英文版】-[美]Walter.Rudin.pdf
The scarcity of cross products on Euclidean spaces.pdf
申屠老师应该是刚入学的同学们能见到最热衷于与同学们讨论数学的老师了。至于为什么上了他的课就知道了。
大概是第九节课(10月中旬),进入本学期重点内容 “几何变换” 以后,他就基本不吹水了。
这节内容老师讲了快两个月,讲得真的得非常慢(个人觉得有些慢过头了),不过对大一学生极其友好。
感觉 “几何变换” 这一节申屠老师讲得有些缺乏逻辑。有那么几节课,老师都是在从不同的角度讲几何变换与矩阵的关系,但是主线不够明确,给人以混乱的感觉。
推荐学有余力的同学们课下自行购买李尚志老师的《线性代数》(也就是妮科下学期 线性代数A 的教材),阅读行列式(第三章)、矩阵的代数运算(第四章)和实对称方阵的正交相似(9.4)几节内容,想读的还可以读一读线性空间(第二章)。申屠老师囿于课程所限只能涉及二阶、三阶的行列式和方阵,对不少性质的解释都只能浅尝辄止(比如说矩阵乘法的结合律、\(det AB = det A det B\)、三个向\(R^3\)中的向量线性相关当且仅当它们组成的行列式 \(det = 0\))。如果你能提前了解上述内容,你听这部分内容就能有一种居高临下的轻松感。
居然还有同学在期中评教中说申屠老师作业多?去看看隔壁班zc老师的作业量吧,你们知足吧。
讲到射影几何(12月初),申屠只有6节课了。
第一节课,他首先告诉了我们射影几何在几何证明中的射影定理,从第二节课开始,他才引入射影几何的严谨定义。讲得真的很自然,很流畅!
隔壁班zc老师就直接从抽象定义开始讲起,据说搞晕了不少同学。相比之下,申屠老师讲射影几何就好太多了。
确实,射影几何相当容易学晕(毕竟射影空间的定义就很奇怪),不过如果把前面的线性变换真正能搞懂就还好。
最后一章 拓扑学简介 不考,老师只会在最后一节课做一个吹水式的介绍(感觉介绍得有点少)。
最后附上一点有用的东西
2024秋季学期期中考试和期末考试分数分布直方图,试卷在https://www.zhangjy9610.me/USTCdata.html
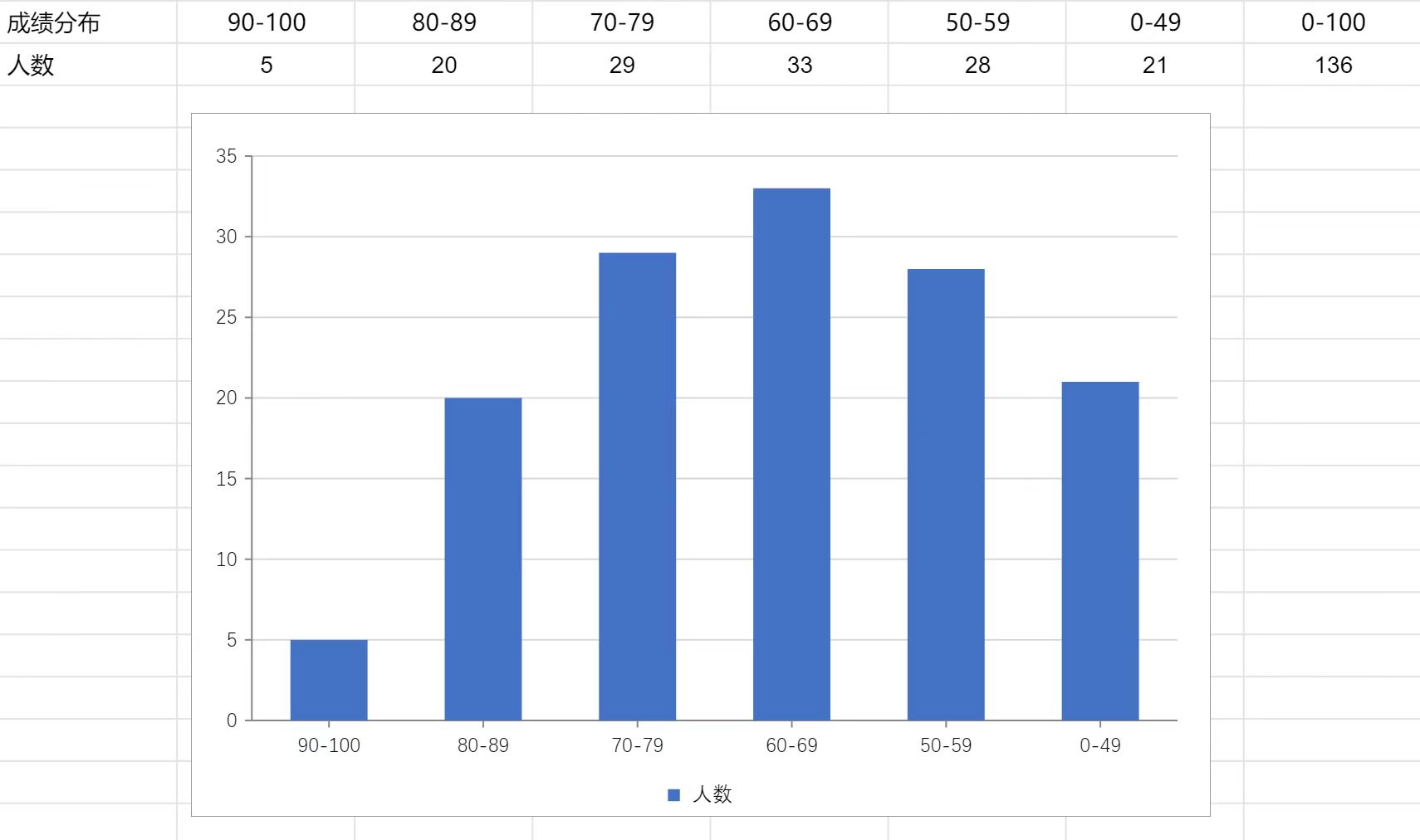
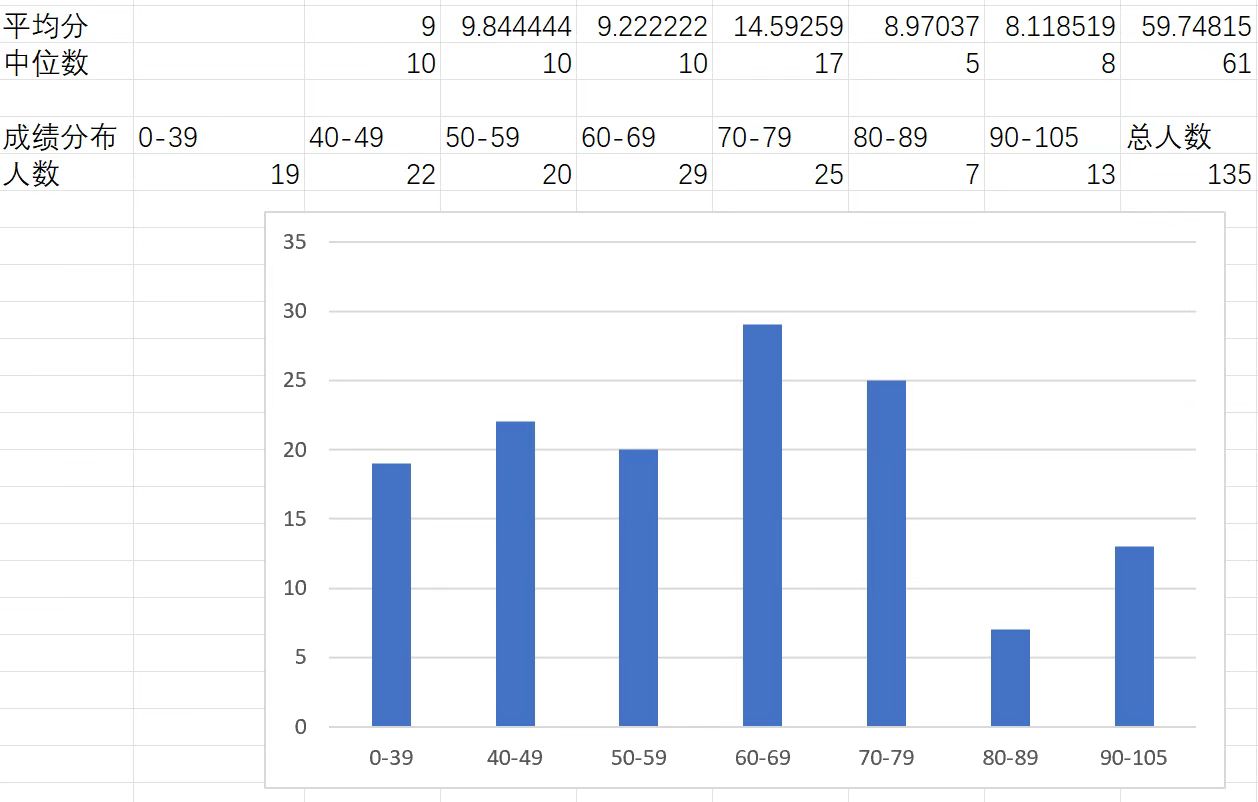
Last but not least, 两位助教 jky, yyc 真的超级好!
每次作业都是认真批改的,每节习题课都是认真准备的,每次讲课都是富有热情的。
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:很多
都给我选申屠!作业两周一交,提前两周结束作业任务,想交就交,这样的老师去哪找?上课从来不点名,讲着讲着跟你讲个黑洞出来,并且还是哥哥的真爱粉——“然后我唱跳rap了一下”。都给我选!
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:很多
看到ywy助教在王老师下征集一些意见看法,突然想起来这样一门很钟意的课程当时忘记评价,同时由于未来也想申请本课的助教,就此对相关话题发表一些本人的看法。
本人修读的是申屠老师的班(当时是赵晨老师,申屠老师两班),修读之前没有接触过任何线性代数理论和其他大学数学知识,修读过程中线性代数知识也仅仅靠几基和代基两门课补充。本人能力自认为不算最强的一批,在后续课程中难题经常做不出来,但在此课程期中89期末95最终总评96。以下内容全凭一年前的印象写的,可能有些许疏漏错误望理解。
之前3学分的课我认为很好,我并没有听到说“很多学生抗议”。可能是我接触有限,但也有可能是,小部分反对群体发声,大部分支持现状群体不发声的现象。这种情况在今年的PDEODE排课中发生过离谱的情况。当然改成2学分感觉上也没啥问题,核心的内容似乎都保留了,减负也可以理解。
我不清楚王老师的课是怎样的。但从风评来说两位老师在本门课上的水平应该是接近的都很高。就申屠老师的课而言,我觉得这是一门安排合理且对我有引路意义的课程。
从知识层面来看,最重要的事,这门课带着我从之前熟悉的几何走向更严格的描述,或者换句话说,从几何中一步步发现线性代数以及埃尔朗根纲领中几何中的群。(而不是先给代数理论再解释),印象最深的就是当时讲三维旋转的时候过渡到了三维矩阵特征值。用申屠老师的话说,“我希望以后你们在学线代的时候,能偶尔想起这门课”。我觉得是很好的实现了的。利用代数方法才能将线代研究推向深入,这不假,但是对于初学者,几何意义可能更能明白他的初始动机。同时呢,也教会了必要的空间解析几何知识,射影几何理论等等。如果开一个两学分三学分的解析几何课程,必然沦为大量技巧和计算的堆砌,这样大概0.5个学分解析几何占比个人以为刚刚好。
更重要的是从思维层面。申屠老师讲解的时候采取的是牺牲一些严谨性,而采用启发式引导式的讲解。比如从什么是直线引导球面几何上不同的性质,从梅涅劳斯定理证明中只需要少量的一些线性性质推广到只要满足这些性质的都有梅定理。类似问题一步步带我养成了从定义出发、抽象化这样的思维方式,从高中那种技巧堆砌逐步走向大学数学的思维模式。这种教学方式对于后续专业课程可能显的慢了,但对于大一学生,个人觉得起到了一个至关重要的引路作用。
要说课程有什么小问题那总不能是完美的。比如老师介绍历史介绍了两周半的量我觉得似乎有点过多,在2学分的课程中应该有所改进。但综合来看我觉得这是我大一甚至可以说目前对我思维提升最大的课程。不提前学线代完全可以跟上,考试题似乎也没有对线代那么强依赖(至少我那年是)。如果在课程教学的进度上能跟着自己看看线代那当然效果最好,但这个不一定就要学校老师教,也不一定非把线代压倒大一上,6+2+2+5对一般大一小登有点超模了。
当然个人在本门课上的学习也并不完美,考试这东西考多了就知道实力固然重要但运气成分不小。未来希望申屠老师or王老师能收我当助教,能够共同学习进步也让这门课变得更好。
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:一般
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:一般
辟谣stjc有进步奖,本人现身说法,期中五十多+期末接近满分=总评86,最后拿了3.7
(叠甲:本人无意参与楼上对此的讨论,只是陈述事实,我认为这样的得分应当是非常正常的给分,期中确实考太差了)
申屠老师讲课非常好,两位助教其实都很耐心负责,总体而言本人课程体验非常不错,课程内容实际上对我有相当大的吸引力
火箭的几基讲义今年终于出版了。突然回忆起两年前上几基时,很多人都在喷这门课。虽然这门课目前已经缩减了,但内容应该还是往年的真子集,这里稍微说一下我对这门课的看法。
其实抛开挤占线代A的时间不谈,私以为这门课还是有一定存在价值的。第一章讲几何公理化,有助于扭转高中一定程度上存在的“轻视概念定理证明而唯独重视计算”的观念,正确认识现代数学的研究方法。虽然这部分作业对初学者或许有些繁杂,但学完大概还是有收获的。
至于第二章到第五章,的确是老生常谈的线代A0。如果在大一上没有修读线代B1,之前也没学过线代,个人强烈建议学有余力的同学找本 李尚志 或 其他任意一本线性代数/高等代数的主流教材 自学,并不需要学得多扎实,能粗略掌握线代B1的基本内容就差不多够了。掌握基本的线代知识能有效提高对这门课的理解,应付作业和考试也更加游刃有余。
第六章拓扑学就是图一乐,想学的建议找本正经的拓扑学教材看。火箭的拓扑学讲义是极好的中文学习材料,同时做到通俗易懂且内容丰富。孙学长的主页也有往年火箭拓扑的课堂录像。
最后提一下,申屠老师的授课水平自然是非常高的,满分不用解释。
- 课程难度:简单
- 作业多少:很少
- 给分好坏:一般
- 收获大小:一般
- 难度:简单
- 作业:很少
- 给分:一般
- 收获:一般
跟舍友聊起几基GPA,又破防了,期末90分绩点3.0。进步奖什么的信不得一点。期中65期末90,总评一看79,是我期末太高了所以没调分吗?甚至加权之后总评变低了。这个老师课上讲得很好风趣幽默所以给6分。
- 课程难度:困难
- 作业多少:中等
- 给分好坏:杀手
- 收获大小:很多
- 难度:困难
- 作业:中等
- 给分:杀手
- 收获:很多
重修选手
萌新慎选,建议自学线性代数。助教gg习题讲义很用心,认真学会有不少收获,但是对于不想学数学的同学就没太大必要了,毕竟难度不小。老师也很好。
出分了再说
逆天,半期期末都在平均分,给分2.3,说是平时分不行,说明老师还是会捞你,只要你写了作业
老师还不错,但是不建议不学数学的人选
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:很多
刚刚考完期末,大抵事爆炸了罢,趁出分前还算冷静,来写个点评。
对这门课的初印象不算太好,毕竟一开始是hilbert公理化以及配套的难评作业,对这门课真的提不起什么兴趣。后来,学的东西又回到了相对符合几何直观的一些内容,但是作业里依旧有一些让人不适的题目(毕竟只会大致想象却无法严谨证明是一件令人难受的事),让人讨厌的点真的挺多hhh
不过,尽管这门课有这些那些让我不喜欢的点,我依然认为这是一门有意义的好课。
引用任广斌老师的一句话:“你只能代表你自己”,以下则是我对这门课的一些粗浅理解:
首先,公理化是一件很有价值的事情(尽管hilbert的作业真的很ex)。这就像在土壤里埋下了一颗种子,这颗种子的一些性质,可以传递给未来长出的大树上——书上对于\(\mathbb{RP}^2\)上的对偶原理的证明就是很好的体现,当然还有申屠老师上课说的现在机器证明啥的
其次,这门课有很多值得思考的细节,确实让我学到了不少东西。比如,在学习内积的时候,可以发现很多熟知的结果并不是依赖某种特定的内积结构,而是由内积的定义决定的,又比如,对着射影对合想了十几分钟然后发现要学习对角化……可能是我的知识并不丰富,这门课确实给予了我不少学习的动力(悲)
最后,这门课带给了我关于线性代数在2维和3维的几何向的理解,这让我认知中的线代也亲切了很多。也让我在看一些证明时有了更舒适的体验,比如书上\(\mathbb{RP}^2\)上一般位置定理的证明,可读性和优雅程度都不错。
hhh没有学过线代,对这门课的理解大概是不深罢,但是一门能够引导人思考的课,我觉得是很值得选的
PS:看了一下丘维声的解析几何,感觉橙皮的可读性还挺强的hhh,以及,申屠老师作为年轻人,课堂也挺活泼的
刚查完卷,看老师在那里给同学查卷才发现老师是真的在捞同学们了(虽然我没有在查卷的时候又捞到分),而且老师还会在查卷的时候讲一些数学理解上的东西,也挺有意思的,这回是真的很推荐申屠老师了!
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:很多
趁着还没有期末考来写下评,总之,无脑选申屠准没错!!年轻,活泼,上课时不时玩梗活跃气氛,以其幽默而不失条理的风格将几基这门课程变得十分美妙而有趣。虽然鄙人期中考的没脸见人,但不影响对这门课,以及申屠老师给出极高的评价! 总之,选申屠,绝对不会后悔! (后续出分再来改改) ┄┄┈┈┈┈┈┈┈┈┈┈┈┈┈┈
考完了,(感觉上比期中好一些?兴许是学习了线性代数的缘故,当然,希望不要只是我的一厢情愿…)。 之前都是夸的,现在写点对这门课的建议吧。 课程整体主要有两个难点,其一是学期刚开始上的希尔伯特公理体系,要求从数个给定的公理一点点推出整个欧式几何大厦的一角。你可能会陷入用长达一页的篇幅,以及如立交桥般曲折的路径,去证明一个过去看起来再简单不过的定理。但一个好消息是,这一章的内容不考… 第二个难点便是后半本书讲述的普通几何变换到射影几何。鄙人认为,若学习过线性代数的话,其实并不算难,相反,你可以在绝大多数结论中见到线性代数的影子,并用相关知识证明。而射影几何本身是一个十分美妙的事物,在书的最后部分(拓扑除外,这学期并没有讲,而且真的,好难…)你讲看到用射影几何对于一些关于点,线关系的定理的优雅证明。当然,我所看到的也仅仅是其冰山一角,但无妨让我体会到它的美妙。 (等出分随缘更新,希望申屠能宽恕鄙人期中过于离谱的成绩,降下神的奶力!) ┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈
出分了,总体来说还是奶的,主要是因为期中考的过于离谱,总评恰恰够上优秀。 所以,还犹豫什么?冲冲冲!
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:很多
期末出分了,遂来pksq写写收获和我无处诉说的感慨()
可以说,数院大一第一学期的课都超乎预期的好,特别是几何学基础,可能确实会有反馈课程没有很深入的涉及几何,但个人感觉还是很有收获的
期中前主要讲的是向量空间(度量,内积,范数)欧氏空间的一些变换,后半学期会涉及低维射影空间和一点点拓扑科普。
申屠老师上课板书真的特别棒,工整而且字很大,后面也完全看得清,上课会很有条理,不会严格按照书上讲,会找一些刚好理解的方式来讲解也会有一些补充申屠老师上课会玩梗(这就是为什么他会有这么多表情包吗)课堂氛围很轻松,真的是上完力学以后非常好的放松TAT
作业方面的话,申屠老师班上作业真的很少,助教也都非常负责!会很认真的敲答案和批作业(甚至还有小红花印章)作业整体难度不大,但比较需要严谨地书写过程
考试方面:期中考和期末考的难度题量都适中,只要认真完成作业就没问题😊申屠老师会狠狠捞。重点来了:一定要去查卷!申屠老师真的会满卷子给你找得分点的!查完卷以后老师会给一个比较综合的评价,申屠老师一直特别包容,即使考得不太好也会指出问题然后跟你说已经做的很好了!真的是特别关心学生的老师!
这一学期的课就这样结束了,很遗憾没有办法继续选申屠老师的线性代数课程。不过,能在学习开始的时候遇到这样的老师,也是一件极其幸运的事了吧,他告诉我们如何真正地去思考一个问题:它是否有意义?一个命题到底告诉了我们什么?最基础的概念需要最严格地推敲,还有就是,严谨性:往往出错的地方就是奇点。那就这样告别吧,可以带着这样的思想一直走下去。
助教在上习题课的时候跟我们说:几何是产生问题的地方。
最后的总结:可以无脑冲!打十分是因为满分是十分🙃
- 课程难度:中等
- 作业多少:中等
- 给分好坏:一般
- 收获大小:一般
- 难度:中等
- 作业:中等
- 给分:一般
- 收获:一般
申屠老师的课还是挺有意思的。
不过针对这个课程,不是很能理解为什么要把它排在线性代数前面学??要么就在课程中多讲一点线性代数知识。
尤其是在射影几何那章,大量用到线性代数知识,书上附录只会列出几个概念,平时也不会专门讲线性代数的知识,本人对这块是模棱两可(看的和听得多了导致会套用,但是还是不会线性代数)然后期末考试大部分是射影几何的,全是用线性代数在算,几何在这就提供了个题目翻译条件成线性代数开算,有啥意义吗?本人期中85,期末因为不会线性代数只有平均分69(倒数第二题20分考的完全是线性代数的东西,直接爆零),分值还占这么大,参考其他人的给分,看来这道题直接把总评从4.0干到3.3,原来不是学不会几何学基础,而是没学线性代数。
- 课程难度:中等
- 作业多少:中等
- 给分好坏:一般
- 收获大小:一般
- 难度:中等
- 作业:中等
- 给分:一般
- 收获:一般
我敢保证 去年肯定是存在进步分这个政策的 单纯说明一下情况 打个9分吧
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:很多
本来挺喜欢st老师的,现在更喜欢了(我不是小黑子)。
本课程作业量轻松,两周交一次,不知道为什么有同学反馈作业多,当然也可能是因为国庆时布置了过多习题,不过多数后来被留作了思考题。补交不要过了zj的斩杀线。
本课程在24秋亦有着线代A0的美誉,换句话说:如果同学有线性代数的基础或基本理解,在本课程的几何变换与射影几何部分会有更佳的体验。不过这不妨碍stjc老师授课的高水准。
Plus: 本课程于25秋改革为半学期,2学分。
- 课程难度:简单
- 作业多少:中等
- 给分好坏:一般
- 收获大小:一般
- 难度:简单
- 作业:中等
- 给分:一般
- 收获:一般
公理化实在是酷!在数学系渐渐开不出课的科大,能学习一门知识面很广的几何课,真幸运。不过平面几何和立体几何倒没什么新鲜的。
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:很多
今年大概是没有进步奖了,确实对期中期末都好的人不太公平
本人期中60,期末87,总评3.7,期中糖丸了考这么低
本来挺喜欢申屠老师的,现在更喜欢了
- 课程难度:困难
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:中等
- 给分:超好
- 收获:很多
申屠老师上得太好了!给分特别奶!但是不建议大一选这门课
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:很多
申屠老师人真的很好,问问题的时候有一种“如沐春风”的感觉,讲课也十分亲切。申屠老师课上既有宏观视角如几何空间如何决定宇宙,也有微观视角即具体的技术细节,十分nice!课程难度也设置的不错,不是很难,同时也需要动脑,属于那种偶尔落下几节课也没什么事的(别打我orz想好好学还是要认真听),所以听起来就比较随性,挺符合我口味的。
总之,申屠老师讲的真的很好!
- 课程难度:困难
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:中等
- 给分:超好
- 收获:很多
从我为数不多的现场上课次数来看(这是可以说的吗)老师讲的很好,给分也很好。
助教很负责,作业有延期了补交也没扣分,习题课讲义对考试复习很有帮助。
我个人gpa低的原因完全是因为自己大一上太摆烂了,考试前连什么是射影变换都不知道,昨晚跟同学讨论后发现就因为这个期末第五题没做出来,白白扣20分qwq,现在看我期中期末在考场上时候的表现都太弱智了…
跑题了,期中期末成绩75/65,作业延期一次,总评80/gpa 3.0。
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:很多
出绩了,已4,有事烧纸(
---
很有意思的一门课,申屠老师也是一位很有意思的老师,「假设我手里有一个篮球,然后我唱跳rap了一下」非常好笑(((
老师布置作业不算太多,虽然题是很难(火箭讲义特点).老师给分很捞,给人提升很大(((
讲课风格上,申屠老师是做代数的,科普拓展了很多内容,非常有意思
总之见着申屠老师,选就完了!冲冲冲!
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:很多
别问,选就完了。 上课从不点名,可以随便划水。 想认真听的话,老师讲的特别好,听起来一点都不累。板书非常好看,偶尔会拓展一些。 作业两周交一次,一个学期就交了6次(作业量不大,但是想认真做的话还是要花点时间的,毕竟课程特色)。 强推强推,我不允许有人不给10.0 希望线代能选上qaq
- 课程难度:困难
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:中等
- 给分:超好
- 收获:很多
申屠老师太好了,真的很好,希望下学期线代也能抽到他。 但是对于垫底进科大的数学废物苕皮来说,几何学基础对我还是太难了。上课睡觉玩手机太多了导致的,是我不好,申屠老师是最好的。 建议有线代和群论基础的人选几基。
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:很多
申屠老师人超级好。10分是给老师的。 至于这个课程,我感觉安排在大一第一个学期不是很合理,起码得学完线代,有些基本的线代知识,这个课才会比较好学一点。
- 课程难度:中等
- 作业多少:很少
- 给分好坏:一般
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:一般
- 收获:很多
一个学期没去上过课,网课嘎嘎爽,从来不点名,两周交一次作业,寝室起早八轮流交。选就完了。
出分了,期末就五十多,但结果捞到了83/ 3.3,虽然期中90多,但还是优秀应该是凑不上的,好捞
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:很多
st老师的魅力无需多言!~
有机会上他的课绝对是荣幸~~(喜获老师签名,开心!~)
正好95 4.3
几何学基础建议好好看讲义(考试范围里的),好好做课后习题,提高思考速度,提高熟练度
关于这门课的上课内容抑或是这门课的历史演变,前人之述备矣。我认为这门课要是想要变得对同学们更有帮助,需要处理好这门课和线性代数课程的关系。
王老师规定,只有大一的同学可以不限制的在作业和考试中使用线性代数知识,高年级的同学只能用上课出现过的那些,似乎老师想强调这门课不需要提前学习线性代数。但一方面,掌握线性代数对理解这门课的授课内容有极大帮助,另一方面,从应对考试的角度来说,熟练掌握矩阵运算或者知道一些矩阵标准型的求法(比如正交相似对角化)非常有用。看似不让我用线性代数,但我直接在试卷上把结果写出来也没什么问题。
没学过线性代数让这门课许多授课内容没法深入展开,或者停留在抽象的例子。但真的学了线性代数又会让这门课许多东西变得太过简单(第三章我基本没听)。后续如果要继续改革这门课可能需要重新安排数学系线性代数的课程顺序以及内容。