2026春 2025春 2024春 课程号:CS200201
- 课程难度:中等
- 作业多少:中等
- 给分好坏:一般
- 收获大小:一般
| 选课类别:计划内与自由选修 | 教学类型:理论课 |
| 课程类别:本科计划内课程 | 开课单位:计算机科学与技术系 |
| 课程层次:专业基础 | 学分:2.0 |
数理逻辑是计算机科学技术的重要数学基础之一,本课程是计算机科学技术专业本科教学的数理逻辑基础课程,主要介绍数理逻辑的基本理论和形式化技术,为后继课程奠定必要基础。主要内容包括:命题逻辑的(标准)形式公理系统(命题语言和形式推导)、语义学和元理论(命题演算的可靠性和完全性);一阶逻辑的(标准)形式公理系统(一阶语言和形式推导)、语义学和元理论(一阶谓词演算的可靠性和完全性)。
考试与作业
侯嘉慧老师的《数理逻辑基础》考试被多位学生描述为“恶心”且“麻烦”。不只是概念题,还有繁琐的推理题和直接证明题,前者需要严密的逻辑推理,而后者由于其复杂性令学生感到为难。特别是直接证明题,是学生普遍认为最难的部分,而与之相关的题目往往需要更多时间。然而,有学生提出通过“运用演绎定理的思路再转写消除其痕迹”的方式来规范直接证明,提高解题效率。
课程内容与教学水平
课程主要涵盖命题逻辑与一阶逻辑的基本知识,其中涉及较深奥的概念,对于数学基础较弱的同学可能较为困难。不少学生表示自学效果好于课堂听讲,因为课程中的很多概念和证明非常抽象,使得不易理解且难以消化。此外,一些学生提到教材的习题有助于掌握课程内容,而老师的课上教学对于一些学生来说收效甚微。然而,作为科大独特的必修课程,其教学深度仍受到一些学生的赞赏。
给分与学习态度
学生对给分情况的意见分歧较大。部分学生认为给分合理,尤其是对没有积极参与课堂和作业的学生也能给出不错的成绩,显示出老师对整体分数的助益作用。另一方面,有同学指出给分不佳,认为与自己的付出不成正比。
学习建议
由于《数理逻辑基础》考试较难且偏重理解和应用,考前不宜突击,建议学生在学期初就开始扎实学习。多位同学强调多刷题、熟悉题型和提高解题能力的重要性,尤其在考试条件下的思维和答题能力显得尤为关键。另建议打印老师的PPT及提前熟悉其中示例,以备不时之需。
课程整体评价
总体来说,《数理逻辑基础》是科大一门复杂但值得挑战的必修课程。虽然学生反馈对课程教学的直接效果褒贬不一,最关键的知识点和技巧需要依靠自学和多做题目来掌握。考虑到只有两学分,学生们普遍认为通过合理的学习策略和复习安排,即便课程难度较大,仍可以获得一个合理的成绩。
- 课程难度:中等
- 作业多少:很少
- 给分好坏:一般
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:一般
- 收获:很多
不知道自己多少分,故也就无法评价给分好坏。
稍微评价一下今年期末考的卷子,比往年的会恶心一些,体现在两道应用题,和判断题的一些坑点。但反正理解了,而且概念之类的认真翻翻看看,这张考卷也没什么难的。
回忆一下考卷(如果还有记得更多的可以在评论区说一下):
第一题:判断题(每题 3 分)(不保证顺序)。
(1) 对于一个公式 \(p\),若有 \(\vdash p\),则对于任意公式集 \(\Gamma\),都有 \(\Gamma \vdash p\)。
(2) 一个公式 \(p\) 是公式集 \(\Gamma\) 的语法推论,则每个让 \(p\) 为真的赋值都会让 \(\Gamma\) 里的所有公式为真。
(3) 用一个项 \(t\) 去替换原子公式 \(p\) 里的自由出现的变元 \(x\),得到的新公式里会有约束出现的变元。
(4) 忘了。
(5) 忘了。
(6) 给定解释域 \(M\) 后,对于一个给定的常元 \(c\),存在两个不同项解释 \(\varphi, \psi \in \Phi_M\),使得 \(\varphi(c) \ne \psi(c)\)。
(7) 忘了。
第二题:忘记了,一个繁琐的推理题。
第三题:给出如下命题的直接与间接证明(18 分):
\(\vdash (p \to q) \to ( (p \to (q \to r)) \to (p \to r) )\)
第四题:在谓词演算 \(K\) 中证明如下两个命题:
(1) \((p \to \forall x q) \vdash \forall x (p \to q)\)。
(2) \(\forall x (p \to q) \vdash \forall x \neg q \to \forall x \neg p\)。
第五题:将如下公式化为前束合取范式:
\(\neg ( \forall x_1 R_1^2(a, x_1) \to \exists x_1 ( \exists x_2 R_1^3(x_1, x_2, b) \to \forall x_2 \exists x_3 R_2^2(x_2, x_3) ) )\)
第六题:证明如下命题:
一位客人要么坐一等座,要么做二等座,而一位客人坐一等座当且仅当其富裕。并且存在客人不富裕,那么有人坐二等座。
优雅至极的一门学问,之后有空再来细讲。(仗着科大估计没人做正统的数理逻辑,发表自己拙劣的见解)
先写点课程内容,也算是给自己复习。我没去上课,自学主要看的书是复旦大学的教材:郝兆宽、杨睿之、杨跃《数理逻辑:证明及其限度》,下面的语言有的地方可能会和书上不一样。
数理逻辑最初的想法来自 Leibniz 构想的通用文字纲领。我们这门课主要学习了其中最基本的部分:命题逻辑 与 一阶逻辑。可惜的是,在 20 年培养方案改之后,数理逻辑从三学分变成两学分(估计是被量子物理给夺去了学分),删掉了数理逻辑的绝对高峰:Gödel 不完备定理。
命题逻辑以一个一个命题为基本单元,分为语义和语法两个部分。
语法这边,上来先给出了三条公理,然后马上就来了整个数理逻辑基础课里面让大家最头疼的 “直接证明”。“直接证明” 这件事本质上是在做语法游戏,它规定命题演算体系 \(L\) 下的一个内定理 \(\varphi\) 是而且只能是一个可以通过一列有限个字符串,里面的要么是 (L1)、(L2)、(L3) 三条公理,要么是可以使用分离规则 (MP),得出的。但是“直接证明”实在是过于繁琐,所以又有了演绎定理、反证律和归谬律来帮助大家简化证明。
说到 “直接证明” 为什么不能使用演绎定理,即使是在题目一开始直接当作引理证明完也不能用。本质上还是这个东西是不合规的,你这个玩意不符合那套语法规则。这里可以说一下 “内定理” 和 “外定理” 的区别:“内定理” 又叫 "元定理”,大概就是这套语法规则里可以玩出来的东西,比如 (否定前件律) \(\neg q \to (q \to p)\),以及大家在习题里看到的各种各样的神秘字符串;而 "外定理“ 大概就是人类通常理解的定理,比如在书上反复用到的归纳原理就算一种 “外定理”,当然演绎定理这些也是 “外定理”。
从本质上来说我们不能在直接证明里使用 “外定理”,是因为命题演算系统 \(L\) 它的语言没办法说明这样一个 “外定理”。比如说,\(L\) 连自然数都无法描述,怎么使用归纳法。“外定理” 实际上是我们在用自己熟知的语言和逻辑,去研究一个 “对象语言 / 逻辑”——命题演算系统 \(L\)。就比如说如果你用了演绎定理,你要怎么根据这个使用了演绎定理的间接证明来写出直接证明呢?至少我觉得反演回去的工作是 non-trivial 的,比你突然想要用 (否定前件律) 了,然后把 (否定前件律) (这个是 “内定理”)的证明抄一遍用上去要困难得多。更别说还要以演绎定理为基础的反证律等。
所以其实我大部分时候,做直接证明题,最感到烦躁的不是不能用演绎定理,而是大致的逻辑链条已经清楚了,但每次用到 “内定理” 却要把其直接证明抄上去。
说了这么多,其实我们已经大致上把命题逻辑的语法部分讲完了,接下来再来看语义部分。这部分显得就特别直白了,可以直接列真值表了!熟悉的与或非也回来了!这部分整个下来是顺风顺水的,后面的合取析取范式,对偶公式等甚至数电就已经学过。
再来是命题逻辑 \(L\) 的完备性和可靠性,这是一个小的高潮,它告诉我们:语义与语法是统一的。完备性指的是:每个在人看来很对的命题,也就是重言式,都可以在 \(L\) 中用那套语法规则玩出来。这个是对 \(L\) 表达能力的刻画,它可以推出我们想要的东西。而可靠性则更进一步要求了 \(L\) 别推出我们不想要的东西:每个 \(L\) 的 “内定理”(可以用语法玩出来的东西),都要是重言式。
证明可靠性相对容易,只需要发现 (L1)、(L2)、(L3) 都是重言式,并且对 (MP) 也封闭即可。
而证明完全性,我们要先进行一个转化:
引理:下列命题等价:(1) 如果 \(\Sigma\) 一致,则 \(\Sigma\) 可满足;(2) 如果 \(\Sigma \models \alpha\),则 \(\Sigma \vdash \alpha\)。
依此我们可以将完全性定理的证明转化为去证明每一个一致集都是可满足的。而后者的证明又有:
Lindenbaum 引理:每一个一致的公式集 \(\Sigma\) 都可以扩张成一个极大一致集 \(\Delta\)。
做法就是把可数多个公式一个一个尝试往里加。有了极大一致集,我们容易从中读出一种赋值:\(\bar{v}(\varphi) = 1 \Leftrightarrow \varphi \in \Delta\),这样我们就证明了完全性定理。这两个定理给出一个附属结果:命题逻辑 \(L\) 是可判定的,你想要判定是否有 \(\Sigma \vdash \alpha\),只需要列真值表就可以了,虽然这样很慢。
书上还提到了别的一些杂项,如唯一读法引理,和其他的命题演算系统(极小系统和 Heyting 系统),由此引出直觉逻辑:否定排中律可以无限制地运用。Gödel 的另一个著名理论是:直接逻辑的真值种类必须有无穷多个。由此可见直觉逻辑与经典逻辑的不同。
接下来到了一阶逻辑(谓词逻辑),它是命题逻辑的扩充。命题逻辑以整个命题为基本单位,这无法接触到个体对象,使得量词无法介入。一阶逻辑定义项集,以原子公式为基本单位。
在语法部分,一阶逻辑比命题逻辑多了几条公理。我看的书里是没有 (Gen) 规则,科大的书里是有的。我暂且觉得没有 (Gen) 规则更好:一个是更加清楚,有 (Gen) 之后演绎定理和反正律都要额外加条件;另一个原因之后在语义部分会提及。这部分倒是没有 “直接证明” 题了,估计是太过复杂了。
语法这部分还要注意理解自由出现和约束出现,以及各种东西能不能替换,这个是一阶逻辑引入量词后必须注意的一部分(哑元的艺术)。
到了语义部分,和命题逻辑不一样,一阶逻辑的语义不再是 trivial 的真假赋值。为了细化一阶逻辑中个体对象的部分,我们必须引入解释域 \(\mathfrak{U}\),让常元对应集合上的一个元素,函数对应集合上的函数,谓词对应集合上的关系。而有解释域还不够,因为变元的值还没有被确定,所以还要再来项解释 \(s\),并扩充成整个公式集的解释 \(\bar{s}\)。
有了这个那 \(\Sigma \models \alpha\) 怎么定义呢?我看的书和科大的书定义是不同的:

当然每个人感受不一样,可能有的觉得科大书上的定义很自然。
接下来又到了可靠性与完备性的环节,同命题逻辑一样,一阶逻辑的语义和语法也是一致的。对于可靠性定理还是去证明各个公理和 (MP) 都可以,只不过花的工作更多一点。
而对于完备性,我们先把一阶逻辑 \(K\) 进行扩充,添加可数个新常元,变成 \(K_c\)。并且添加 Henkin 公理:\(\exists x \varphi \to \varphi_c^x\),其中 \(c\) 是新的常元,而 \(\varphi_c^x\) 表示把 \(\varphi\) 中所有自由出现的 \(x\) 替换成 \(c\) 得到的公式。
可以这么理解 Henkin 公理:对每一个存在性的语句都添加一个直接证据 \(c\),所以扩充 \(K\) 和添加 Henkin 公理的目的都是 “消去量词”,使得从中可以比较容易的读出一个可能的解释域和项解释。
我们记 Henkin 公理集为 \(\Theta\),可以证明 \(\Sigma \cup \Theta\) 还是一致的,这时候我们在和命题逻辑一样,运用 Lindenbaum 引理,将 \(\Sigma \cup \Theta\) 扩充成极大一致集 \(\Delta\),从这一公式集中容易读出一种解释域和项解释:
(1) 论域 \(\mathfrak{U}\) 为 \(K_c\) 上所有项的集合;(2) 一个谓词 \(P\),其对应 \(\bar{P}\) 为:\((t_1, t_2, \ldots, t_n) \in \bar{P} \Leftrightarrow P(t_1, t_2, \ldots, t_n) \in \Delta\);(3) 函数对应和谓词类似;(4) 常元 \(c\) 直接对应于自身。
这样可以验证我们就找到了一个解释域和赋值,如果一阶逻辑中还包含等词,我们需要考虑由等词划分得到的商集。然后还是根据命题逻辑中的转化,我们由此得出完备性定理。
与命题逻辑很不一致的地方是,\(\Sigma \vdash \alpha\) 这件事在一阶逻辑中变得不好弄了。命题逻辑只需要列真值表,但是一阶逻辑中解释域和项解释都是无穷多的,也就是解释个数的区别。实际上,一阶逻辑是不可判定的。
PS:数院的陈卿老师说过:
不要碰数理逻辑和集合论这种形式化的东西,水太深。
由此可见数理逻辑的深邃。
- 课程难度:中等
- 作业多少:中等
- 给分好坏:一般
- 收获大小:一般
- 难度:中等
- 作业:中等
- 给分:一般
- 收获:一般
放一个将 “使用演绎定理的证明” 转写为直接证明的算法:
假定我们现在已经有了 Γ∪{p} |- q 的证明序列 (q_1,q_2,…,q_n=q) , 想要写出一个 Γ |- {p→q} 的证明序列. 我们知道直接证明的定义虽然是链式的, 但它实际上有着如同二叉树的结构: 从最后的结论往前回溯, 每一个公式要么是由它之前的两个公式 MP 得到, 要么是一个公理/条件. 所以我们可以把证明序列 {q_n} 写成 (非完全) 二叉树的形式. 以下是一个示例:
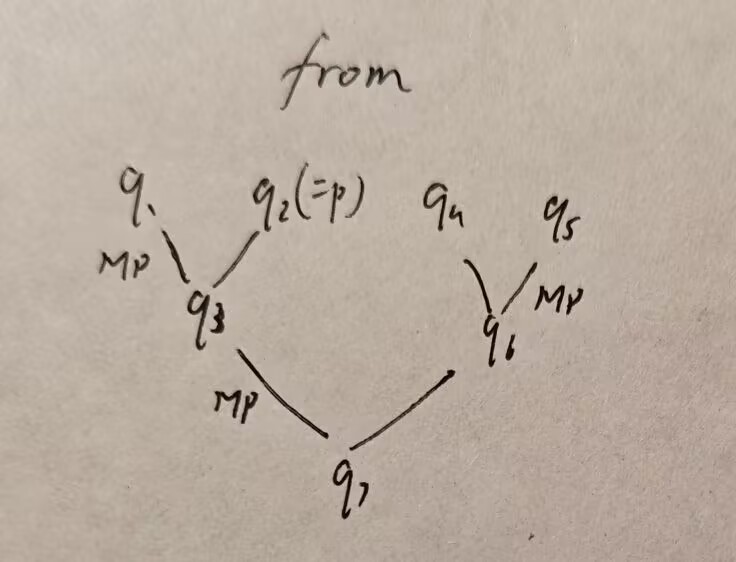
显然, 在没有条件 p 时, q_i 不一定都为真, 但 p→q 是一定为真的, 所以我们把这个二叉树中的所有 q_i 改为 p→q_i . 现在只剩下两个问题: 1. 每一个叶子上的 p→q_i 如何得到; 2. 已知 q_i 与 q_j 通过 MP 得到 q_k , 如何用 p→q_i 和 p→q_j 得到 p→q_k.
我们首先回答第二个问题: 由于 q_{i,j,k} 是一个满足 MP 所需形式的三元组, q_j 一定形如 q_i→q_k (或者相反, 但这里 q_i 和 q_j 地位是相同的, 无需另外讨论) . 我们可以先用 q_i→q_k 结合公理模式 L1 通过 MP 得到 p→(q_i→q_k) , 再用公理模式 L2 写出 (p→(q_i→q_k))→((p→q_i)→(p→q_k)) , 连续 MP 两次得到 p→q_k (下文中将这整个过程称为 “衍生 MP” ) .
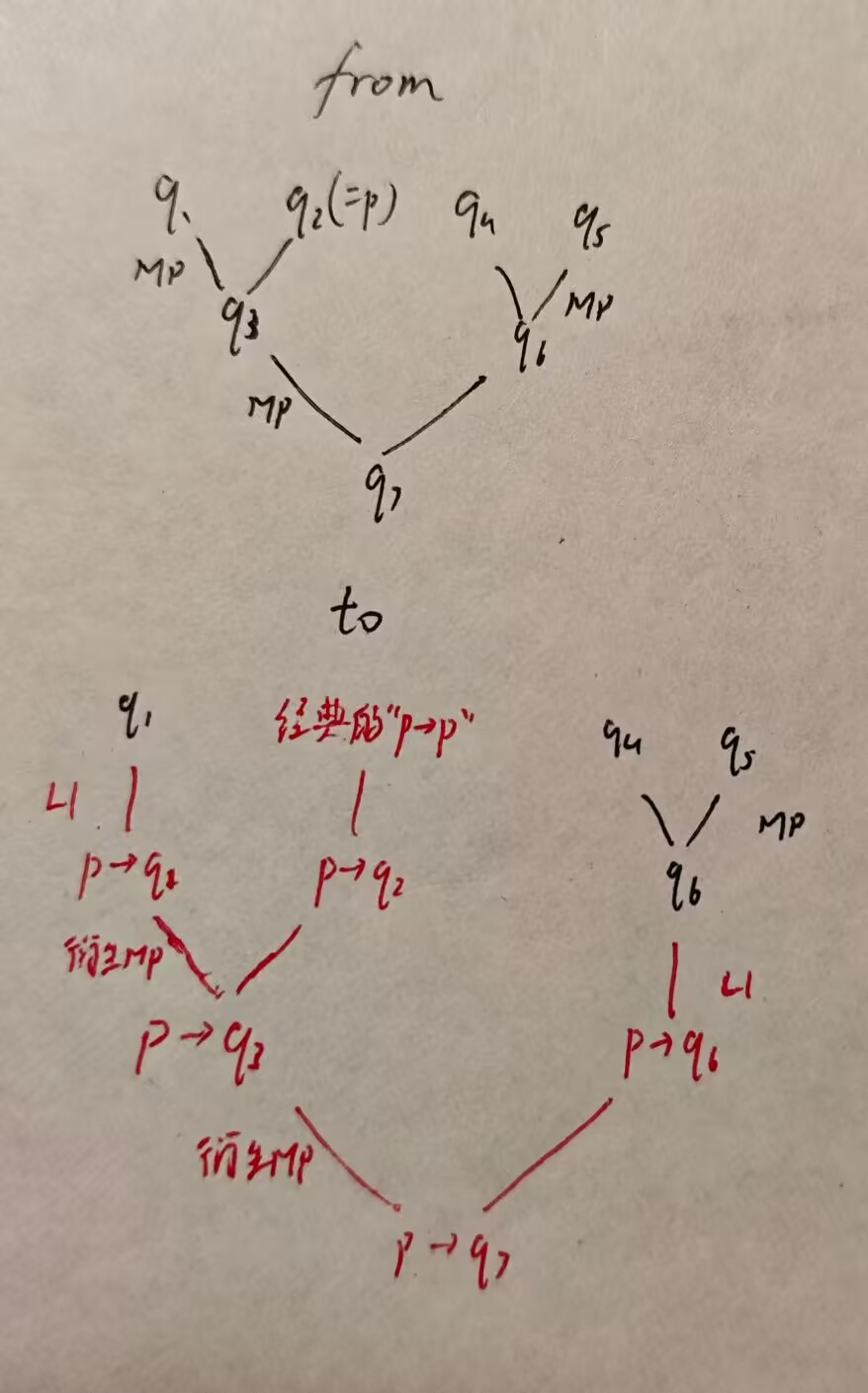
对问题一的回答是容易的: 对于每一个在原证明中处于叶子的 q_i , 如果 q_i 本身是公理或者属于 Γ, 依然可以直接写出; 如果 q_i 本身就是条件 p , 则可以背诵一套经典的内定理 p→p 的证明.
最后, 注意到对条件 p 的引入采用 “一滴血原则” , 即对于某个中间公式 q_i , 只有当它或者它的引理证明中用到 p 时才转写成 p→q_i ; 如果 q_i 在没有条件 p 时也成立, 那么直接照搬原证明中对它的证明序列即可. 但是, 如果发现它紧跟着的下家需要转写, 也需要再用 L1 把它变成 p→q_i 以便后文证明. (例如下图的 q_6 对 q_7 的作用.)
由此我们得到新证明的二叉树 (注意在这个二叉树中, 每一次推导使用的是衍生 MP 而非 MP, 所以写出来的公式数量会多很多) :
下面我们展示一个具体的例子 ∅ |- ((p→q)→r)→(q→r). 在这个例子中我们使用了两次演绎定理, 那么往回转写两次即可.
连续演绎定理拉回两次, 我们改为证 {(p→q)→r,q} |- r . 这个题的直接证明是容易的:
① q 条件
② q→(p→q) 公理L1
③ p→q ①②MP
④ (p→q)→r 条件
⑤ r ③④MP
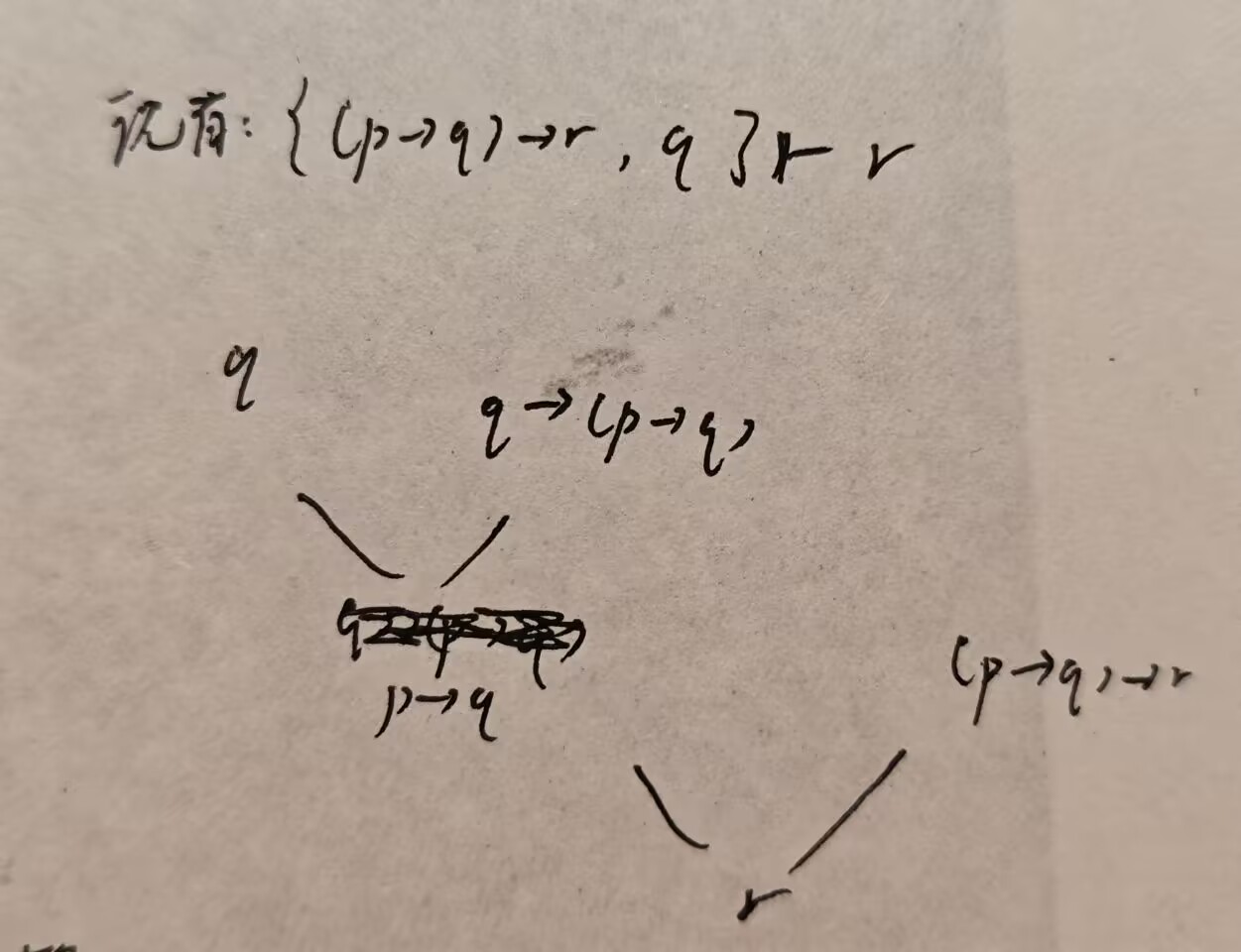
现在进行第一层转写, 即试图写出 {(p→q)→r} |- q→r 的直接证明.
我们回顾证明序列的每一个公式, 在前面添加上 “q→…” 试图重现整个证明. 注意到 ③ 做如此改写后形如 q→(p→q) , 本身就是一个公理, 没有必要再从改写后的 ①② 推出. 所以我们先写出 ③' : q→(p→q) 随时备用.

再看④, 由于 (p→q)→r 本身是条件, ④' q→((p→q)→r) 可以联合 L1 做一次 MP 轻松得到. 我们把这个过程列出来:
① (p→q)→r 条件
② ((p→q)→r)→(q→((p→q)→r)) 公理L1
③ q→((p→q)→r) ①②MP
再拿出我们准备好的 ③' :
④ q→(p→q) 公理L1
现在, 上述 ③ 和 ④ 已经具备 L2 所需的形式, 可以开始衍生 MP :
⑤ (q→((p→q)→r))→((q→(p→q))→(q→r)) 公理L2
⑥ (q→(p→q))→(q→r) ③⑤MP
⑦ q→r ④⑥MP
现在开始第二层转写, 即直接证明原给命题. 我们分析上述序列的二叉树结构: ①②MP③, ③⑤MP⑥, ④⑥MP⑦. 这里用到条件的本质上只有①, 并且注意到 ①→③ 实际上形如公理 (就是②) , 所以没必要再去转写 ①→① 和 ①→② , 直接先准备好 ①→③, 然后列出⑤⑦, 用一次 L1 做出 ①→⑤ 和 ①→⑦ , 连续 “衍生 MP" 两次即可.
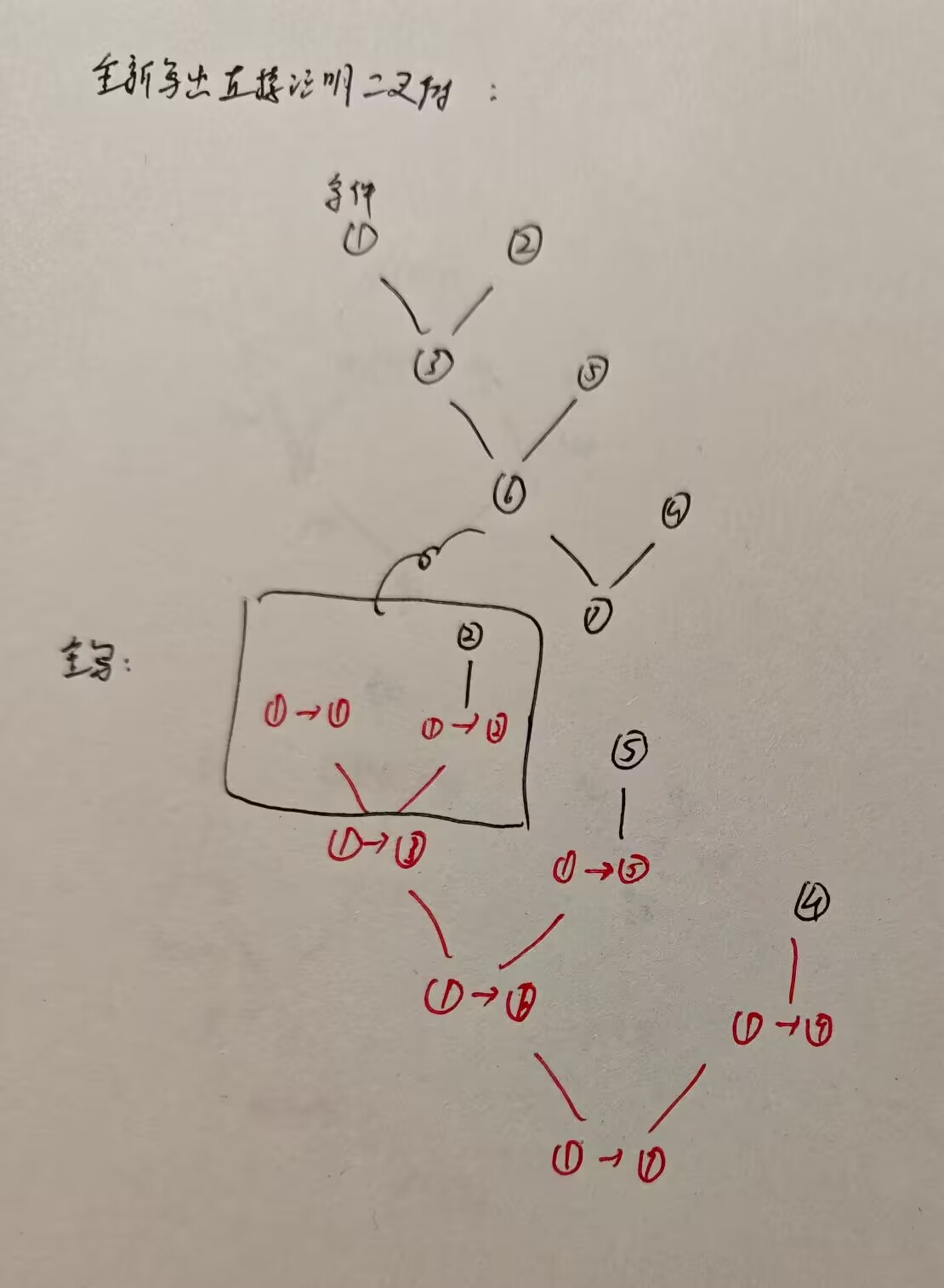
总结一下: 这里我们给出了一个在直接证明题目中 “先使用演绎定理寻找思路, 再转写消除演绎定理痕迹” 的工具.
需要注意两点:
1. 我们偷渡出来的工具只有演绎定理一条, 不包括反证律, 二次否定等, 用这些二级结论找到的思路需要寻求别的方法合法化;
2. 尽管这种算法可以直接证明任何命题, 但我们没有必要机械地照搬算法的每一步, 而是可以随时注意转写出来的哪一步本身就形如公理, 从而不必再转写其上层; 也没有必要一上来就用算法库库抄, 可以先自己想想思路, 划归到一个形式简单, 但证不出来的引理后, 再用算法来处理这个引理, 或许会更节省时间.
最后建议考前看到这条的同学, 如果想要在考试时使用这种方法, 最好还是自己找几个公式来练一下手. 读过了算法及其证明并不代表理解乃至熟练了整个算法思想, 如果没有手操经验, 考场上可能会在某一步不知道自己此刻要干什么耽误时间.
- 课程难度:简单
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:简单
- 作业:很少
- 给分:超好
- 收获:很多
????????????
- 课程难度:困难
- 作业多少:很少
- 给分好坏:一般
- 收获大小:一般
- 难度:困难
- 作业:很少
- 给分:一般
- 收获:一般
刚考完期末怨气很大,上大学以来的第一篇评课,就决定是你了,数理逻辑!
先说一下本人的情况。我平时从来没听过课,也没看过ppt,作业靠看课本也差不多能写出来。我提前几天就开始复习数理逻辑,书上题目基本上都掌握了,但是考试和我想象中的截然不同。
第一大题是判断题,比较常规。
第二大题就开始恶心了。题目给出了ABCDE五个人和他们之间的关系,还要求用范式作答。我们都知道,有五个变元时真值表就有32项,光是用真值表算就已经很麻烦,如果还老老实实一步一步化简的话写起来极巨而复杂,因为条件之间是合取的关系,所以要化简成合取范式,再转为析取范式,最后判断真值指派。思路非常明确,但是写起来非常麻烦!!
第三大题,超级恶心的直接证明。早在考之前,我就听说直接证明很难,题目放上来,想吃的自行品鉴吧
\(p\rightarrow{((p\rightarrow{\neg{p}})\rightarrow{\neg{q}})}\)
第四大题是谓词演算中的证明题,没看
第五题是把公式写成前束范式
第六题是应用题,需要把条件转换成谓词演算里的公式,再判断结论是否正确,然而作业题里根本没练到类似的题目。
考前,我觉得平时作业会写,而且开卷,能难到哪去呢?考完后我才知道,平均分六十多总是有原因的。这些题目单拎一道出来,或许花点时间总能磨出来,但是在考场上,缺乏熟练度的下场就是,前面的题目画了太多时间导致后面的题目根本没时间写,而那些题目或许才是真正好拿分的。
来看评课社区的各位应该大多是考前突击的,我想说,不管平时学的怎么样,如果考试不能发挥出来,那都是白搭。最终成绩=掌握程度x考试能力x给分好坏,掌握程度主要取决于平时下的功夫,给分好坏取决于老师怎么样、班级怎么样,到了期末周,这两项很难改变了,最需要注意的,就是提升自己的考试能力,如何制定科学的复习计划,如何发挥出自己的实力,尽可能多的拿分。
还有就是,一定要多刷题、多刷题、多刷题!数理逻辑是这样,其他的科目也是。只有刷题量到了一定程度,才能拿到题就有思路,上手就能写。考试的时间很紧张,每题多花几分钟,可能最后就写不完了,所以做题的熟练度非常重要。
最后,这门课只有两学分,没考好也不用灰心——
没时间为数理逻辑的逝去而哀悼了,接下来感到战场的是——计算机组成原理!
希望大家都能取得自己满意的成绩吧,复习去了。
- 课程难度:中等
- 作业多少:中等
- 给分好坏:一般
- 收获大小:一般
- 难度:中等
- 作业:中等
- 给分:一般
- 收获:一般
温馨提示:课本后面是有习题答案的
- 课程难度:困难
- 作业多少:很多
- 给分好坏:杀手
- 收获大小:没有
- 难度:困难
- 作业:很多
- 给分:杀手
- 收获:没有
计科最烂的数学课,上课一点用没有,还有不少数院佬来炸鱼
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:一般
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:一般
我这学期几乎一节课没去(除了某次去交作业的时候听了半小时),全靠看书+写作业自学,最后拿了4。
- 课程难度:中等
- 作业多少:中等
- 给分好坏:一般
- 收获大小:一般
- 难度:中等
- 作业:中等
- 给分:一般
- 收获:一般
没什么用的课,学完就忘完了,但是这个老师没点名,没小测(可能上课做一点不交的小测),期末给分还行,如果置课这个老师也没必要换,都是考前速通的,比图论还没有学的欲望,随便对付对付就行。
- 课程难度:中等
- 作业多少:中等
- 给分好坏:一般
- 收获大小:一般
- 难度:中等
- 作业:中等
- 给分:一般
- 收获:一般
考试的时候一般可以直接skip掉直接证明,因为就是证不出来。
一定要记得打印老师的PPT的最后一个part,那里面有谓词推理的格式要求和示例,而这一部分书上是没有的,考试最后一题还必考这个推理,如果没打印就只能像当时考试坐在我旁边的同学一样面对最后一个题想半天一个字也写不出来,最后无奈像沙摩柯一样弃牌了。
至于老师的讲课,确实是听不下去,so这学期全程没听过课,作业也没做明白过,全是用gpt帮忙写的。最后考试一天速通的,拿到3.7也可以接受。
- 课程难度:中等
- 作业多少:很少
- 给分好坏:一般
- 收获大小:一般
- 难度:中等
- 作业:很少
- 给分:一般
- 收获:一般
点开课程群绷不住了,怎么这么多大三数院✌求佬们手下留情😇😭😭😭
更新:直接证明没写出来,其他题目可能有小问题,判断不知道,勉强优秀,已经满意了,毕竟也就两学分,老师、助教人还是挺好的,尤其是封助教,赞一个