2025秋 2024秋 2023秋 2022秋 2021秋 2020秋 2019秋 2018秋 2017秋 2015秋 课程号:PHYS6003P01
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
| 选课类别:基础 | 教学类型:理论课 |
| 课程类别:研究生课程 | 开课单位:近代物理系 |
| 课程层次:硕士 | 学分:4.0 |
2022年、2024年秋季学期,讲课内容主要是微分几何。
参考教材:Frankel的The Geometry of Physics;
2023年秋季学期,讲课内容主要是李代数。
参考教材:Georgi的Lie Algebras in Particle Physics。
教学内容
杨焕雄老师的《现代数学物理方法》课程内容主要涵盖微分几何、拓扑学、微分流形、李群和李代数等数学物理领域关键概念。课程内容包括微分流形、李导数、黎曼几何、李群定义、李代数的根和权及其在物理中的应用,尤其是在粒子物理中的用法,如SU(2)、SU(3)等。这是非常重要的知识,尤其对理论物理研究有帮助。
教学风格
杨老师的讲课细致且语速适中,PPT制作精美且内容详尽。尽管一些学生建议他加入更多例子以帮助理解,但整体上杨老师的课程细致且内容清晰。课堂上,杨老师从基础开始构建复杂概念,尽力使得内容易于理解。
作业与考试
作业量较少,通常为课程内容的推导或简单应用。作业批改认真,鼓励使用LaTeX等系统提交作业。期末考试题目侧重于基本概念计算,较少涉及复杂推导,通常为开卷考试。考试整体难度不大,通常可以在讲义中找到所需公式。有学生提到,考题虽然计算量大,但主要是基础题,这使得学生即使在复习不全的情况下也能取得不错成绩。
给分情况
给分非常慷慨,不少学生反映,尽管对部分内容理解有限,最终还是得到了不错甚至是满分成绩。平时成绩对总评有较大影响。
适合学生及推荐理由
推荐理论物理方向的学生,尤其是对微分几何或李群等领域有浓厚兴趣者。课程不仅能为学生在该领域的进一步研究打下坚实基础,而且给分较好,降低了选课的学业风险。
课程反馈及建议
尽管课程质量和给分受到广泛好评,但仍有学生建议增加课堂实例和课程内容扩展,以便为学生提供更丰富的学习经验。选课前确认当年的讲授主题(微分流形或李群李代数)是明智之举。杨老师即将或已经退休,但他的教学模式和宋代影响值得在该课程中继续延续。
- 课程难度:困难
- 作业多少:很少
- 给分好坏:一般
- 收获大小:很多
- 难度:困难
- 作业:很少
- 给分:一般
- 收获:很多
2022年秋季学期选购(雾),这学期讲授的主要是“数学物理中的微分几何与拓扑学”(摘自老师第一讲的PPT)
~~然而讲的其实主要是微分流形,拓扑学讲的非常少~~
本学期总共有五份PPT(相当于是五个单元),简单列举如下:
- 微分流形(讲微分几何和流形的基本知识,引入切空间和余切空间)
- 李导数(主要讲推前-拉回映射,然后引出了李导数和内积算子,最后给出了Cartan三公式及他们的证明)
- 联络与协变导数(主要在说张量场,包括协变微分、协变迁移,关注坐标卡有关的计算;在2最后还引入了曲率、挠率,结构方程,并推广到四脚标架上进行更一般的计算)
- 黎曼几何(这一章内容很多,前半段在讲引入度规之后的黎曼流形,并利用经典电动力学作为例子展示了我们如何用张量方法描写物理;而后将第三章中的内容放在黎曼流形上讨论,并引出了Killing矢量场和共形变换;最后讲了一点广相的内容当作黎曼几何的例子)
- 黎曼几何中的超曲面(这一章主要在讲黎曼超曲面,给出了其投影诱导出的度规;后面很大一部分精力在处理内禀曲率张量,和由此引出的Gauss-Codazzi方程组;在最后讲了四维时空的3+1分解,作为超曲面的一些例子)
以上大约是一学期的内容,实际上授课从第二周开始,第十五周结束,没有上满一整个学期;其实感觉尤为可惜,因为课堂内容中还是有相当多的地方可以进一步拓展(依稀记得浣熊曾经说过会讲到一点de Rham上同调理论,但是最后可能是因为备课压力问题,没有上成);以及作为例子的物理部分感觉还是可以多一点。
考核方式是20%作业+80%开卷考试。
作业方面,浣熊的作业量不是很大,一般都是课堂上一些内容的推导,或者是一些很简单的运用,一到两个题;如果能够熟练运用课堂内容,作业应该用不了一个小时(然而,“熟练运用”非常不容易,以第二章为例,Cartan三公式和很多的引理用来在导数算子、内积算子、李导数和矢量对偶运算之间的转换非常有技巧性,有些证明是相当困难的)。作业批改完全由老师自己完成,可以课堂提交纸质版(每五道题交一次作业)或者BB系统提交电子版(只接受LaTeX,Word或Markdown等排版作业,不接受扫描件和过大的手写PDF),一般一道题满分10分;如果有些题目做得很认真,浣熊会给出加分(一般一道题的bonus是5分,并不难得到,我就在前期被扣了十几分的情况下硬奶了回来)
因为疫情现在还没考,考试有关的情况开学考完来补充。
总之,这门课作为旁听还是很推荐的;选课的话,因为教务处已经调整了政策,现在本科生选择这门课,既不能当作毕业学分,也不能与研究生共同计算优秀率,所以无论怎么看都不是非常好的选择。
顺便吐个槽,这门课开课的时候80人正选,教室坐的满满当当,源源不断有人来找老师签字增选;老师一开始说“你们先别着急,先听几节课再选”。期末的时候就只剩下60个人(只剩7个本科生了,本来有十几个的)。
考完了。寒假时惊悉浣熊老师已经办理了退休手续,并且据他本人所说,这门课以后应该会由其他老师接手,所以不出意外的话这是浣熊老师最后一次讲授这门课了。考试的内容不是很难,基本上都是基础的计算,需要用到的所有公式在讲义上均可找到,并且没有什么拐弯抹角的方法(难度甚至比作业还要简单些)。因为大家都没太来得及做完,还延长了半小时。感谢浣熊老师本学期的精彩讲授,这条评课也许不能为后续选课的同学提供什么帮助了,但是我还是私心地想借此纪念一下杨焕雄老师在科大的贡献。 也希望每一个物理人,特别是理论物理人,能有一个让自己安心的去处。
- 课程难度:简单
- 作业多少:很少
- 给分好坏:一般
- 收获大小:很多
- 难度:简单
- 作业:很少
- 给分:一般
- 收获:很多
研究生课一直评论较少,我来说两句。
这门课主要侧重李群,但是还是会先从群论基础群表示论讲起,后大半学期着重讲李群李代。教材是georgi的lie algebras in particle physics,老师补充了很多书上省略的推导内容。
上过杨老师电动量力的同学应该了解杨老师的授课风格。ppt做的详细精致,上课语速较慢,胜在足够细致能够听懂,课下不用花多余努力。这门课更加佛系,作业量也极少,由于没有助教老师只收了一次作业就没有管过了,期末直接发了他做的georgi书习题解答小册子。起初我是想翘课自己看书的,结果发现书远没有杨老师ppt的推导细致,配合课程食用效果更佳(如果不打瞌睡的话)。
众所周知朱界杰老师的群论讲到后面就开始起飞了,稍不留神就一头雾水,而且朱老师内容广泛,真正想学好需要课下花一些时间去吸收。所以建议以后学习群论的同学两门课配合食用。这样的话基本只需要花一门半左右的努力就可以搞定两门课,对群论这个数学工具有一定的掌握了。对于想看goergi那本书的同学也建议选一下这个课监督一下进度,而且不明白的地方可以迅速补充,由于课程要求较佛系也不会形成负担。
ps: 如果我回到本科时代我会两门群论加上高量一起选TAT ,可惜我们学校除了极少数热门的研究生课外鲜有评论。
---------------------------------------------------
更新下成绩,自认为没有学太懂,但是多亏了老师手下留情居然拿了个不错的成绩...题目确实比较契合内容,没有为难大家
- 课程难度:中等
- 作业多少:很多
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很多
- 给分:超好
- 收获:很多
本学期的内容主要是李群和李代数,前四周会提到群论基础和有限群表示的基础,之后会先介绍几个简单的李群有关的定理与例子,但主要的内容放在李代数上,特别是根的分类与从Dynkin图构造李代数,以及从基础表示出发的张量形式和相关的计算。
参考书用的是Georgi,留的作业也是Georgi上的题。ppt可以作为一个Georgi的解读和细致的版本来看,因为Georgi上推导很多跳的很大,自己看容易看不懂,ppt大概覆盖了上面的1,2,3,4,6,7,8,9,10的一部分,11一部分,12,13的一部分,差不多半本书吧。
ppt合集:
Please login to download the attachment‘
习题解答合集(不全):
Please login to download the attachment
期末考试不算难,除了那道证明题小题之外,其余都是计算题和简答(定义)题,但事实上不需要什么计算,因为大部分题都有类似的例题,写得快的话大概一个半小时左右就能写完。第一题是循环群有关的,会定义和基本性质就行。第二题是spin-j表示的张量积的分解系数(CG系数),这里面的最高权方法上课会详细提到,而这道题甚至有部分就是上课讲的,剩下一部分就是作业原题。第三题是SO4群的定义表示的验证以及基本性质,同时证明SO4同构于两个SO3的直积。第四题是最高权方法构造李代数和正根,原题。第五题是用Young Tableaux表达SU5的CG分解,同时计算直和表示维度,作业原题改了个数。
期末给分也挺好的,但一定要注重平时分,本人做作业的时候经常想不明白就写或者写的很不清晰,导致虽然写了几乎所有附加题但只获得了折算后92的作业分。作业每周留3~5道左右,但难度比较高,有的甚至不太好理解题目在说什么。一般是用latex交。
不需要除了数分线代之外的其他数学基础,而且杨老师一直讲得极其细致清晰,听课的时候让人心情舒畅,大二大三的本科生肯定能听懂。不过有些内容(比如WE定理,张量积表示,基础表示的张量形式之类的)可能需要结合一些物理意义。
- 课程难度:简单
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:简单
- 作业:很少
- 给分:超好
- 收获:很多
第一次在pksq写点评,之前一直都懒(bushi),实在是因为hx给的太多了,特来拜谢亲爹
(分割线)
杨老师本学期是讲授微分流形,元姐姐已经详细介绍过了。课程本身设计难度是不小的,可能所限于总课时以及hx特定的语速(适合手动3倍速,意识到bb上支持三倍速就摸掉了好多hh),内容其实不算特别丰富(而且作业可以一直咕咕,本学期我总共就写了三次作业,一次大概一天?顺便能写一下总结笔记方便查找),不过要全部充实地理解可能需要看更多的东西。frankel上其实是一本很适合上手的书,真的是比lcb易懂十倍甚至九倍(悲)。虽然我启蒙是lcb+梁老师b站网课,张量面面观感觉是前五章最为出彩的观点(而且我很喜欢梁书的指标),但是读完以后感觉还是例子少,特别是少图,可能对我来说不够直观吧;相比之下frankel就有好多图图,以及阐释也更自然舒服,还是挺推荐的。————好像歪楼了————其实本来考完试后想和hx聊聊,感觉可以在课上或者课后作业补充一些例子,为数不多的例子就是算球曲率和球测地线方程?总之还是很少很少,感觉没有例子的几何就好像是玩游戏不玩原神......,有些时候不算些什么东西出来感觉理解还是特别浅,非常空虚;可惜得知hx要办理退休了,下学期电动就是最后在讲台上见到hx的机会了,建议学电动的同学可以速冲(虽然我当时没冲,sad),还是非常遗憾,甚至没有听到hx和超对称的故事,sigh
关于考试可能其实也没有太大参考价值了,毕竟以后要换老师,还不知道是哪位,不过可以简单讲述一下期末的破防时刻
由于选课一时爽以及教务处的神奇安排,我的考试周是连续六天一天一门。考到这门的时候刚好是第三门,且与下一门仅间隔一晚上,恰好两门都是三个月没看了(背景介绍)以及hx考前的灵魂拷问
 (乐)
(乐)
考试总共有四题,第一题是求(0,2)型的李导数(贴心送分),第二个是验证内积算子作用在n-form上反对易,第三题比较搞人心态,使用了和往常不同的下标定义,第一问该定义下方向导数分量算子作用在普通函数上(大概是这么个意思)对易,第二问是给了一个矢量场的协变分量,求一个关于方向导数分量算式并验证关于下标全反对称。第四题是求ADS2上的度规并验证其上的kiling矢量场
考试的时候对于第三题印象非常深刻,因为感觉非常怪,在那里抓耳挠腮地想定义到底该是什么,前前后后改了三次,似乎最后一次改成了半对半错的结果(比照答案来看)(其中正确理解的部分也在试卷上出现过但是被划掉了),直接心态爆炸,最后验证killing矢量场的时候已经完全红温状态,验证了一个半就不想继续了(本身前后的考试都很折磨)。考试延长了半小时,但感觉后面已经有些无心作答了,交卷前还突然发现自己疑似伪证......结果是直接在东图沉默两小时,最后九点开始预习下一门,人整个裂开,相当难熬,已经做好了放弃成绩打算
看到答案之后意识到自己似乎并不是伪证,但是把一部分正确答案划掉顿时心痛不已,还是觉得要放弃成绩。但是当hx最后说6个本科生总评都不低于89的时候感觉人傻了,最后总评出4.3的时候感觉更是有点晕
我实在想不明白是从哪里找来的分数,比照量力可能是有一些考试bonus,但是还是,大为震撼,感觉比知道数电总评还震撼,甚至想直接去5403电动课线下磕头的程度(bushi)
最后还是希望杨老师退休生活愉快,以及希望老师能看到他的梦想被实现(bushi)【拜谢】
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:一般
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:一般
浣熊老师讲课虽然很平淡,但若能听得进去,就会发现他对任何概念的阐述都是无比清晰的。课程本身也不是太难,作业很少,考试简单。总体而言体验非常好。
- 课程难度:困难
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:很少
- 给分:超好
- 收获:很多
很有意思的老师!可爱!祝早日康复!


太极拳在意不在形:“就你指出的涉及CG系数的问题,我只能说你列的参考书上的结果是正确的,我给的参考解答上的结果也是正确的。记得张三丰教张无忌学太极拳时是这么说的?太极拳在意不在形。这句话也适合于这个题目。”
课程内容与收获:70%,9
作业:25%,10
给分:5%,10
加权平均:9.3->9
课程内容:今年讲解李群李代数。有限群基础讲了六周,逻辑没有那么清晰,但是勉强能听。事实上感觉这些基础还是有些用的,老师说后面如果还开课不再讲这一块了,需要先学习朱老师的群论课。然后是李群李代数的基本概念,举了一些典型的李群SU(N),SO(N),SO(3,1)等的基础作为例子。接下来是SU(2)群的不可约表示,SU(3)群的不可约表示,SU(N)群的不可约表示。限于课时考试范围就到此为止,后面的内容很多都是结论,作为其他专业的学生已经无法完全跟上,只能先记住结论没有初步的理解,所以后半段就比较难受。“这门课优先服务粒子物理专业的同学。”无论如何总体讲的还是比较出彩的,很有浣熊特色。
作业:不多,5道题左右收一次,交了八次,有几道题目比较力大砖飞(废手)
考试:考试题型依旧类似于作业题,把作业吃透还是比较重要。一道有限群,然后SU(2),第三题是常见李代数的一个例子,相当于验证对易关系之类,后面还有张量表示和杨表(布置这么多题,一看就要考)。后面两题的内容我没有学明白,对着作业答案口胡了一下,已经忘记怎么写的了,也不知道算的对不对,能给多少分。
给分:稀里糊涂学了后面一个多月,能优秀就是爹。这个优秀率,爹!!!爽吃!
杨老师对课程的意见,直接上图:
- 课程难度:困难
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:中等
- 给分:超好
- 收获:很多
午睡起来看见总评给了100 ?!
(震惊)
有空补评
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:很多
2024秋期末考试:
1验证闭形式、恰当形式,计算外积
2给定切矢量和余切矢量,计算导数算子的作用
3三维环面的度规、非0联络、联络1-form、曲率2-form
4题目构造了一个2,1平直时空的一个超曲面,成为一个反德西特空间,计算给定坐标系下的线元,最后一问问killing矢量场
今年的考试题目注重于计算而非推导,没有太大的思维难度,只有最后一问有些趣味。不过最后一问问得有点模糊,给的答案是验证killing矢量,考场上按照解killing方程做的。
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:很多
先占个楼.
非常推荐这门课程!今年的上课内容和22年一样,都主要讲数学物理中的微分几何。大致内容为:
- 微分流形的概念、切空间、微分形式及其外积、外微分;
- 李导数、内积算子、嘉当三公式;
- 张量空间、联络和协变导数、曲率和挠率;
- 黎曼流形的度规张量、等矩变换与Killing矢量场、Stokes定理、广义相对论简介、超曲面与诱导度规;
- 近复流形、复流形(不考).
杨老师讲课的速度适中,我个人认为随堂听课的效果很好(至少思路能跟的上)。本学期的助教也很nice。
平时作业很少,一般大家用不着在课下花太多时间去复习。
期末考试开卷,但是计算量可不小(已经算死了),本来安排的两个小时的考试时间,结果考试时间还延长了半个小时。(就这,Killing矢量那几个题我还没验证完,其他不少计算题我还在改来改去……)
鉴于老师自己的ppt可能会有错误或遗漏的地方,建议大家还是带上Frankel等参考书(比如:今年期末考试考察了闭形式和恰当形式,老师在上课期间是提到过这一点,但这两个概念恰好在杨老师前四章ppt中未出现,导致了一些麻烦)
- 课程难度:困难
- 作业多少:中等
- 给分好坏:超好
- 收获大小:一般
- 难度:困难
- 作业:中等
- 给分:超好
- 收获:一般
这学期讲微分流形,被导师要求去选,然后笨蛋研究生在线破大防。
太难了,真的太难了啊。
有无好心人说说这门课往年的给分情况,会给研究生75分以下的分数吗?
虽然期末考试一路剥蒜一路错,重演了数学物理方程的悲剧,但是仍然被老师奶起来了(感恩!
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:很多
浣熊,我滴超人!虽然没学太明白,但是给分是真的好
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:很多
今年主要讲李群李代数,不过这门课每年讲的内容不一定相同,我听说上一年讲的是微分几何与微分流形,所以有兴趣的同学可以事先了解一下当年讲的内容(第一节课会介绍这学期的讲课内容与方向,可以来旁听),当然无论是李群李代数还是微分几何微分流形,都是物理研究中非常重要的数学知识与方法,杨老师理论功底深厚,课件很用心,一学期下来收获很大,给分也非常好,强烈推荐!
- 课程难度:困难
- 作业多少:很多
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:很多
- 给分:超好
- 收获:很多
物院大二上选购,配合朱老师《物理学中的群论》食用。不考勤,选课105,其中24本科生。
杨老师在qq群里会发上课用的纯英ppt,后半李群部分内容基本都来自《Lie Algebras in Particle Physics》。
课程内容:有限群基础知识,群表示与特征标,置换群与杨图,李群李代数,嘉当子代数,SO3与SON与SUN与SU2与SO(3,1),su2与张量表示与张量算符,嘉当子代数、根矢量、权矢量、su3,素根与Dynkin图和Cartan矩阵、基本权,su3,SU3张量、杨图CG分解,SUN,(以下不考:更多李代数,单李代数的分类,子代数,夸克,SO10),要学会还是要费不少精力的。作业一定要按时做!一旦落下想补上进度要费不少劲。
每章ppt后有习题,每攒够五道布置一次作业,共8次作业,允许布置后2周内交(即习题课前,讲完会发答案)。我的情况是课不怎么上(因为落两周进度上了也听不懂),ddl花一两个小时读完一章约50页ppt,再花一两个小时写完作业。前半部分作业都是读完ppt就会做,后半有几道题需要在前后的ppt里找方法(比如给权矢量分组,分解成直和)。
期末开卷两小时(并加时30分钟),只考到元旦前讲的内容。全卷共5题,每题20分,基本都是作业难度。纸质资料不限,推荐至少印一份so3的cg系数。本人作业分79/81,期末估计100左右,总评100。(研究生课优秀率超高!)
推荐喜欢数学的同学食用,很有意思(这门课的很多内容都在数院研究生课才讲),和《物理学中的群论》有一半多的内容交叉,互相构成补充。
听说这门课每年轮流开李群和流形,希望下下个学期还能听到吧🤗
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:很多
从各个方面来说都是无可挑剔的好课,虽然不是本研贯通,但是推荐理论方向和想学一点微分几何的本科同学来选。
参考教材frankel的书论述较为严谨,内容也很全面,但感觉有点冗长,尝试读了一会读不下去。这里推荐一下梁灿彬和nakahara的两本书,个人认为是对课程内容的很好的补充和延伸。
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:很多
这门课之前我学过广义相对论,自然学习过基本的微分几何知识。但是这门课仍然有许多地方对我而言是全新而有趣的。比如说和微分形式相关的嘉当三公式,(伪)黎曼几何中的挠率,曲率的非坐标形式。尤其是广义相对论的作用量部分,杨老师进行了非常详细和完备的讨论。这让我在课后把frenkel的教科书看了一遍,导师的科研任务都没怎么做…
但是考试比较奇怪,四个题全都是计算题,而作业题几乎都是证明题。第一题判断几个微分形式是恰当的还是闭的,第二题求微分形式的内积和李导数,第三题求torus的度规以及曲率,第四题算adS_2点度规,验证killing矢量场。
我建议选这门课的同学,在熟悉了张量的指标运算,知道了内积算子,李导数啥的作用在张量的一般形式之后,一定要计算一个具体的例子加深理解。在考试第二题,我用嘉当第二公式计算二形式的李导数,所以先算它的内积。就是因为那里算错了,导致我第二题几乎都错了…
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:很多
粒子物理人,在这门课上收获巨大,前来评课。
原本以为杨老师在23年春季结束退休,就没有这门课了,还为此感到难过。当我看到23年秋季学期课程安排有杨老师的《现代数学物理方法》,那么肯定要选。
本学期的内容是物理学中的李群李代数,采用的教材是Howard Georgi的Lie Algebras in Particle Physics(本书是高能物理开放书籍,可以在相关网站https://scoap3.org/scoap3-books/上免费下载电子版)。课程主要内容如下:
- 群论基础(包括最简单的群的定义、置换群、有限群表示的基础内容、杨表方法求不可约表示)
- 李群(定义李群和李代数,介绍转动群和SU(2)的重要例子,加深了对角动量的理解,介绍根、权)
- SU(3)(研究su(3)的基本表示,介绍如何求其不可约表示的基态矢量,用张量方法和杨图方法求张量积,加深了我对重子十重态八重态、介子八重态的理解)
- SU(N)(像SU(3)那样介绍SU(N)的相关性质,同时杨老师讲了Georgi当时的比较热门的大统一理论GUT的一些内容,不过告诉我们GUT已经被证伪了)
相比于纯数学的李群李代数,课程更加贴合物理人的需求,讲授了物理学中比较重要的SO(3),SO(3,1),SU(2),SU(3),SU(N)等具体的李群(李代数),加深了我对量子力学(角动量,当然还有量子场论类似部分)、粒子物理的基本理论框架的理解。
杨老师的作业是很有价值的,很多问题都能加深对课上相关知识的理解。考试是开卷,难度不大。
给分方面,是我来科大三年见过的给分最好的一门课,今年给了大量的总评100,可以看看其他同学的评课。
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:很多
期末总评99,考试估计只有93(很大程度上有浣熊奶的成分),作业还做得不错加上问问题又加上了五分,达到了99。不得不说这个给分还是太权威了,基本上作业做了,考试来了就能给75分以上(其实有两道送分题,即使没做出来感觉问题也不大,只要写了都会给分。)只有两个哥们挂了,估计是实在太摆了,浣熊捞不动了。
关于课程内容,我觉得浣熊的课件做的真的很好。“物理系的数学证明总是不能做到尽善尽美,许多时候我们要采取试探解的方式来求取一个合理的答案” 浣熊老师在课上说的这句话我觉得用来概括这个课程最为合适。科大的学风走向我觉得是有些奇怪的,似乎大家对数学的完备性有一种执着的追求,这我觉得并不是那么的健康,当然也可能是我太菜的原因。
在期末复习的时候,我发现浣熊本次的课是有一个主线的:如何找到表示的不可约空间?浣熊在mmp05的李代数定义提到的一个非常重要的定理:

我觉得作为贯穿整堂课的脉络,非常值得大家的注意,以及后面基础表示的引入:基础表示定义了一个不可约表示。现在看来也是回味无穷。浣熊在在群里的与同学们的积极互动也是很有意思,25秋的同学们也发了截图了,浣熊真的是一位可敬又可爱的老师。
再次也得提一嘴尽职尽责的助教们,每一次的作业都会有完整的习题解答,作业批改的也非常认真,对我的作业错误的地方也给出了提示和指正,非常感谢他们。
作为非粒子物理专业的同学,深刻的理解到了为什么这门课如此受欢迎,希望以后在做自己的工作的时候能多少用到一些群论的东西,也不算浪费了这学期所学。
附上这学期的作业给大家,全部用的是课上学的知识,不会有超纲,希望能对非粒子物理的同学有帮助。
- 课程难度:困难
- 作业多少:很多
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:很多
- 给分:超好
- 收获:很多
老师给了我满分,我也给老师满分()
这门课无疑是极其优质的课程。课程的口子开得很小,只讲授群论中的李群。得益于此,课程的讲授非常清晰详细,内容不算多,但吸收得极好。
老师非常有人格魅力,说话慢条斯理地,时常有种理论人超脱的幽默感。
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:很多
这个学期讲群论,前面一部分讲有限群,后面一部分讲李群,李群是重点。
这门课是物理学中的群论,在数学的严谨性和完整性上有所欠缺(也可能是群论内容过于庞杂),这可能导致学习过程中觉得一些操作和结论很突兀,比如:讲了很多杨图的用途,但是我一直不知道这样的图是怎么被想出来的
教材是Georgi的Lie Algebras in Particle Physics。会按照这本书的顺序来讲,补充一些书里没有提及的内容。可以参考马中骐老师的《物理学中的群论》。
班里的学习氛围很好。群里常有人讨论,也会有同学在群里问其他课或自学时候遇到的问题。者杨老师也很愿意和同学们交流。
考试开卷,比较简单,能从作业和讲义里面找到。给分也非常好。优秀率给了接近80%,本科生可以选这个课刷GPA。
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:很多
目前物院有三个老师三门课程会讲群表示论和李群李代数,分别是朱界杰老师《物理学中的群论》,杨焕雄老师《现代数学物理方法》,以及段昌奎老师《群论及其应用》(这门是博士生课),恰巧三门课我都上过了,正好打包评一下。
段老师的群论课是最世俗化的,大部分定理证明都不会讲,李群也没有给出非常严谨的定义;朱老师花了大篇幅讲表示论定理的证明,还从微分流形引入讲李群李代数,是最数学化的,但前面有限群讲的时间太长了,还要从比较复杂的视角切入讲李群李代数很容易听不懂;个人认为杨老师的讲法最好最中庸,李群是从一个让物院学生相对好接受的角度引入的,而且他不会在细枝末节上纠结很久,不重要的证明会直接留学生自己看,重要定理或结论的证明及应用会不厌其烦地讲。综上,授课方式上朱/段/杨我会打8.5/9/9.5分。
内容上,除了大家都有的群表示论&李群李代数,朱课的特色内容是群作用定理、群的扩张和有限群的分类,微分流形和拓扑也算是;段课的特色内容是点群的应用,比如分子振动模、红外和拉曼光谱,最后一章还讲到了时间反演对称性与磁点群;杨课SU(3)以SU(N)的不可约表示讲的比较深入,为此介绍的权空间和张量表示都是另外两门课程没有涉及的。
给分上,我只能说杨老师是真神😭😭参与课程建设性讨论(比如给课件挑出错误)总评可以加5分,本以为自己总评85+5上90就很不错了,谁能想到出分直接95啊!!全班超过¾的人优秀,实在太顶了✊给分上朱/段/杨我会打8.5/9/10分。
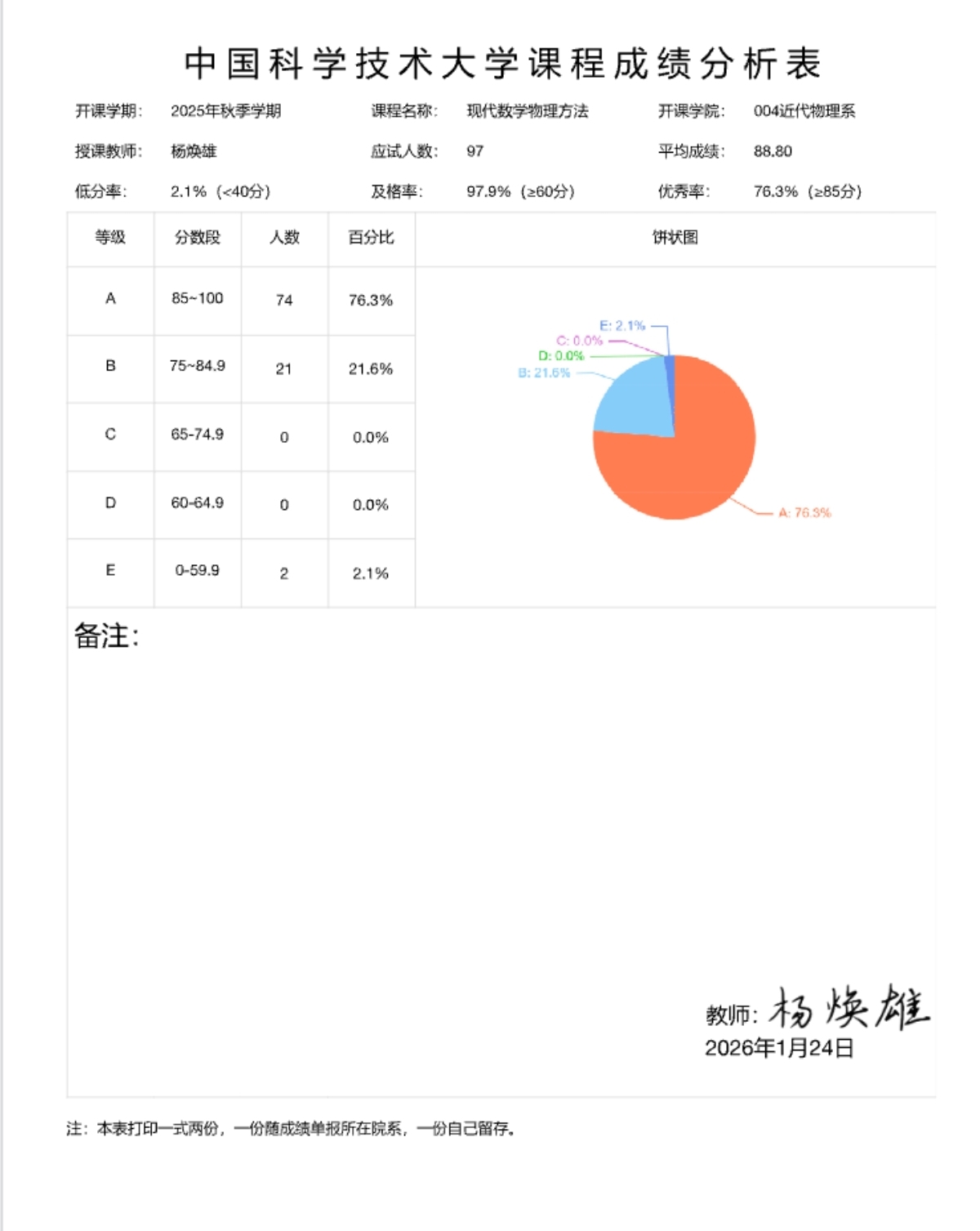
总之,学一学期杨老师的群论课收获颇丰,无论是在知识上还是绩点上,非常推荐想学习群表示论和李群李代数的学生来选!尤其是粒子物理和理论物理方向的,可以解释一些专业上的问题,比如为什么重子3⊗3⊗3=10⊕8⊕8⊕1
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:很多
杨老师讲课节奏和我很适配,虽然用PPT但我却能跟上,同时逻辑清晰,听课体验良好。
作业和考试都没有为难学生,没什么偏题怪题。
给分极佳,大约75%优秀率,伟大不必多言。
杨老师今年应该是真的准备退休了,赶在此之前选了这门课算是我的幸运吧。
- 课程难度:困难
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:中等
- 给分:超好
- 收获:很多
老师很好,讲什么概念都很细致。两位助教也很好,习题课资料也都有回放。
但是笨蛋只有自己能拯救自己😟/(ㄒoㄒ)/~~
考前看作业题还是迷糊,有点破防了,非粒子物理专业的同学还是慎选。