2023春 2022春 2021春 课程号:00170101
- 课程难度:中等
- 作业多少:中等
- 给分好坏:一般
- 收获大小:很多
| 选课类别:计划内与自由选修 | 教学类型:理论课 |
| 课程类别:本科计划内课程 | 开课单位:数学科学学院 |
| 课程层次:专业核心 | 学分:4.0 |
教学内容与方法
李皓昭老师的《复分析(H)》课程内容丰富,讲授内容涵盖复数基础、全纯函数、多值函数、级数、孤立奇点、留数定理、定积分计算、整函数理论及Fourier变换等经典模块。主要教材为史济怀《复变函数》1-7章和Stein部分章节。部分同学认为史济怀书上的习题过于复杂且计算内容不足,建议可辅以Stein的材料进行预习。
教学水平与氛围
多数同学认同李老师的教学水平高且讲解细致,他常在板书上写下详细的证明思路和重要结论。不过,李老师上课速度较快,板书迅速且工整,建议预习以更好跟上进度。一些同学认为李老师上课有冷幽默,会为课堂增加几分轻松感。也有同学反映上课内容多,教学进度较快,前期需适应老师的教学风格。
作业与考试
课程作业难度较大,但主要依据课上例题和指定教材内容。一些同学认为作业和考试题目与讲义内容紧密相关,注重基础知识和计算技巧,建议务必熟练掌握课堂讲授内容和布置的题目。考试题目以复积分基本计算、Cauchy公式应用和定理叙述为主,期末考试需全面复习整学期内容。
给分情况
在李皓昭老师的课程给分方面,意见存在分歧。部分同学反馈给分温和,很多同学成绩高,优秀率较高。但也有同学认为考试略难,均分不高,总评给分一般。总体而言,近年来李老师似乎在调分和分配上更注重最终成绩,部分成绩中等的同学获得了较为满意的总评。
总结
整体来看,李皓昭老师的《复分析(H)》课程教学内容严谨、充实,教学方法细致,课堂氛围较好,适合有数学兴趣和基础较好的同学选修。作业和考试难度中等偏上,但与课程内容联系紧密。若认真跟随老师的教学进度并熟练掌握基础知识,取得好成绩是可以预期的。对于希望深入理解复分析理论和应用的同学,此课程会带来较多收获。
- 课程难度:困难
- 作业多少:很多
- 给分好坏:杀手
- 收获大小:很多
- 难度:困难
- 作业:很多
- 给分:杀手
- 收获:很多
出分了,果然寄穿了...
我当初为啥要头铁退yd啊QAQ
复分析(H)和线代A2都4学分,总评79
重修哪个,是个大问题
这下出事儿了,期末也没过均分,光前两题计算扣了19分。
复习重点放到了最大模和Fourier,结果重点考了留数和整函数。期末复习确实有点赶,26交完通识课论文才开始补天,中途招生还浪费了亿点时间。
按往年lhz的给分,这波估计要3-。
好消息:不用重修线代A2了
坏消息:原因是机会给更低的课了
有点后悔头铁退普通班了,明年重修多半就不选H了。
下学期选的H课可能也要减少了,还是选普班旁听H最友好(
刚查完期中卷,有(bei)感(cong)而(zhong)发(lai)
学期初置在yd,然后lsm又挤不进去,冲劲儿一上来就退课选了H
感觉老师并没有其他评论中描述的“冷淡”,反而有时幽默感上来,还能引发哄堂大笑
讲课没得说,水平杠杠的,最开始觉得直接一句“我们希望...”就引出后面要讲的内容略有生硬,但后来习惯了觉得还不错,能高效利用时间 ~~(开火箭)~~ 。不过既然选H课,很重要的原因也是想多学点东西。
课堂内容量也够大,周四的三连堂差不多20+面黑板,初期和隔壁两个班的进度大致形成等差数列,大概是
lhz:Cauchy公式;lsm:初等复变函数;yd:复数基础
lhz:Laurent展开;lsm:分式线性变换;yd:全纯
期中的题多少还有有点难度的,但很多简单的题掌握不扎实也能扣不少分。
比如我30分的计算就扣了15分;证含参积分的全纯性忘了(内闭)一致收敛;书上一道辐角原理做的例题,我当成\(Rouch\acute{e}\)做了,卡了半小时没出...
说到底还是有点松懈了,本以为复分析会是这学期最友好的课之一,但学了才发现技巧性极强,而且这个班大佬密度也应该是最高的,期中没过平均分,甚至在考虑能否放弃修读...不过据说lhz是由取期末max操作的,还是先学好罢。
还有一个多月就考期末了,希望能“以未来拯救过去”,期末考个高点的分,把期中硬拉起来。 退一万步也要至少拿3.7吧。
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:很多
很多人说,大二下学期里面最简单的一门课是复分析;也有人说,大二下学期里面比较难的一门课是复分析。我个人的理解是,复分析这门课理论结构上其实难度没有实分析和近世代数大(全纯函数的性质实在是太好了!),但是它的知识细节比较多,比较杂,可能不好记忆。
李皓昭老师今年讲课的内容完全按照他第一节课在黑板上写的内容来,评课社区好像也有人发过了,今年李老师飙车把这些内容全部讲完了。个人认为李老师水平是很高的,人有一点冷幽默,总归还是很好的,就是发量不太健康(逃)。不过他上课的速度真的很快,板书快速且工整,建议之后学这门课的同学在上课之前简单预习一下老师要讲的内容,上课的时候接受的能快一些,也好跟上老师的思路。网上似乎有老师2020年的讲义,老师大体上按照这个讲义的内容来,顺序会有调整,讲义上没有的部分对应Stein书的4-6章,老师这部分也是大体按照书讲的,预习可以参考以上的两份资料。
教材方面,用的是史济怀《复变函数》的1-7章(有几节跳过)以及Stein书的4-7章(其中第7章的内容只作简单介绍,考试不作要求)。个人强烈不建议用史济怀书进行预习,且强烈不建议硬刚史济怀书上的习题,事实上老师留的作业题已经完全足够了!如果实在想刷题,不如去做做Stein书上的习题,难度适中且大部分有提示。不过Stein书也有自己的问题,这本书对于复分析的计算方面讲的太少(比如用留数定理计算实积分这块),具体怎么去权衡就看大家自己的理解了。
考试方面,个人理解是一定要熟练掌握基本概念和定理与上课时候讲过的例子,而且计算要准确!李老师对于计算非常重视(如复积分的基础计算,Cauchy公式应用,Laurent展开),期中出了30分的基本计算,期末出了24分,这些分拿不到太亏了!再就是复分析经典题目:叙述(老师读音:xixu)概念定理,期中考试考的辐角原理的叙述,期末考的正规族和Montel定理的叙述,其中期中考试的叙述题好多同学因为定理条件记忆不全而只得了1分(满分3分),后面学这门课的同学一定要记住记忆要准确无误啊!我个人在备考的时候只复习了老师上课的讲课内容和布置的作业题,期中85,期末81,看来熟练掌握上面的内容能保证大家拿到80分吧(大概)。
给分情况尚不明确,据说去年给分一般,但是今年在“新mj精神”的指导之下,能否有所改观呢?总评出来之后我将会更新这一部分内容,届时该项的评分可能会发生改变。
7月10日出总评更新评分,今年给分情况似乎不错,个人4.0,看课程群内的情况老师应该是做到了给大家“都满意的成绩”,所以我直接给李老师评个10.0满分!华班课程的给分优势似乎开始体现出来了吧。
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:很多
人到期末了回想下来这应该是我这学期收获最大的一门课了。
从复数定义到素数定理,李老师今年算是完全按照预期目标讲完了所有内容(除了因为放假放掉了最后一节课,素数定理的证明细节没有讲),并且还在查卷后给我们讲了一节复几何(老师非常鼓励大家入坑)。
课程内容大约是史济怀1-7章,Stein 4-8章,其中略去个别小节(比如Mittag-Leffler变成了一道作业题,Stein第7章细节没讲完)。老师的板书基本与往年那份讲义一致,预/复习起来很方便,不过这样上课也会失去些小惊喜hhh。老师对于书上定理证明的思路解释的十分清楚。
我感到很好的体验在于,老师在期中前时不时补充或者留成作业的一些题目在期中后发挥了重要作用(比如Phragmen-Lindelof定理)。这些内容首次出现(当然在史济怀的课本上可能也是最后一次出现)时会被认为是“奇技淫巧”,待到见过具体应用后才体会到这正是复变理论不同于实变的鲜活案例,我们起初认为是纯粹的技巧也只是因为在实变中培养的直观帮不了太多忙。
最想要吐槽的是,史刘的教材实在令人不满意。大家说的最多的莫过于习题过于困难,我想这背后也反映了传统的教学理念。老一派的信条固然要坚守,毕竟数学很大一部分就是由技巧构成的。但在不厌其烦地玩弄习题之前,应当抽出一些时间注重理论的严格性(观点的现代性)。史刘书对于诸多内容的处理不够严格,讲解不够深入。比如大名鼎鼎的Cauchy积分定理,多值函数Log的定义等等(还有无穷无尽的细节)。对于大大小小的定理也缺乏有启发性的注记。如果这门课能够完全基于Stein讲授(当然需要老师补充一些内容),我想课程会变得更加优雅。
最后说一下考试。今年的期中卷子整体难度适中,考到留数定理以前。期末卷子考察整个学期内容,难度有所提升,不过大部分题目还是比较友好(共8道大题,2道计算,2.5道课上/作业原题的水平)。悲剧的是期中期末平均计算题-7,i抄着抄着就变成1了还有谁?
给分还是很好的,本人期中87,期末94,总评98。老师最后一节课邪眸一笑称大家都对会成绩很满意,另外感觉老师期末查完卷明显变和蔼了许多hhh。
- 课程难度:困难
- 作业多少:中等
- 给分好坏:一般
- 收获大小:很多
- 难度:困难
- 作业:中等
- 给分:一般
- 收获:很多
出分了给老师补个分。
利益相关。笔者期中82期末87(最高分分别是88和94),总评卡线95。看得出今年老师还是花了不少心思调分的,从现有情况看,似乎期末影响比较大。
老师的讲义主要参考史刘和stein,今年的内容涵盖了史刘前7章以及stein的Fourier分析部分,最后几节课讨论了zetas函数的全纯开拓并浅谈了其与素数定理的联系,查卷的时候还开了一堂复几何的科普小讲座。如果能够用心听课,收获绝对是很大的。
老师面相有点凶,但其实人很和蔼。上课的时候废话很少,授课细致且流畅,很多冗长定理的证明都会先给出思路,证完了还会带我们回顾一遍。除开早八这个因素,课堂体验可以用舒适来形容。助教哥哥水平也很高且负责,人还帅(跑题),身披的那一件羽织令我印象深刻,可惜我习题课全翘了(谢罪)。
复分析可以说是数学领域里最优美的理论之一了,简洁与深刻并存,美丽动人。科大传统教材在技巧上下足了功夫,但观点的现代化却缺乏关注,这或许对学生的发展是不利的。在这点上数分B3与几基教材算是做出了很有意义的尝试。
这门课的作业是十分困难的,但是不必为此太过担心,复分析学习的重点依旧是对于诸多概念的理解,基本例子的玩味,以及计算的基本功。笔者认为这也是老师出卷的导向。期中期末都有叙述定理,判断概念的题目,计算题涉及许多基本知识的考查。如果不熟悉单值分支,期中的积分就拿不到分了;如果只会Cauchy积分定理而忘记积分的定义,期末第一题也无从下手。证明题中使用的技巧也没有超出课上例题的范围。总的来说,如果好好听讲,基本功扎实,这门课也能拿到一个不错的分数。
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:很多
今年绝对是风评上升的一年。老师参考了mj精神和实分析事变后,优秀率估计小升了一波。
课程讲了啥其他人都说得很清楚了。个人感觉老师把一些科普性的东西也讲得很生动,虽然零散了点但是老师也尽力帮我们找到框架了(ʘ̥∧ʘ̥)。最后恰好讲完了第一节课定下的目标,所以整个学期学到的东西真的很多,很有收获。
老师真的很友善,出题也不为难我们;上课语气比较温和,给人一种静水流深的感觉。
期中滑铁卢,比均分低了三四分;期末比均分高九分,老师给了91的总评。老师应该挺看期末的。
- 课程难度:中等
- 作业多少:中等
- 给分好坏:一般
- 收获大小:一般
- 难度:中等
- 作业:中等
- 给分:一般
- 收获:一般
本人22春修读这门课,并于23春担任这门课的助教。对于李老师的讲课情况以及这门课包含的内容之前的评论已经说得很全面了,以下只是借此分享一下这门课的学习感受以及一些看法。
笔者认为复分析本身是一门非常elegant的课程,全纯函数定义简单但是具有非常好的性质,可以说整本书的所有内容都是Cauchy积分公式的推论。所以笔者认为在学习过程中应该更侧重于理论本身,对于一些比较细枝末节的条件没有必要太过纠结(比如一些围道的选取实际上可以只用考虑toy-contour的情形,并不需要考虑一般的简单闭曲线,这对后续主要结果的证明已经够用了,并且可以借助一些几何直观也能简化许多叙述)。一些最基本的技术也是重要的,虽然第一次见会觉得很难想到,但也没有必要在初学的时候去死磕(当然每门课都是如此)。
关于习题,史济怀书上的没有必要全部都做,尤其是第六第七章个别题目即使不会做想找答案看看多半也找不到(因为没人会/吃多了撑着)。李老师布置的作业基本上都避开了这些比较钓鱼(?)的题目,把作业弄明白也基本差不多了,没必要见到什么题都要想着去做,做不出来还怪书不好。如果想找题刷的话大可去看一些英文教材,这些书上的题目的风格跟史济怀的又不太一样,有些难的题也会有提示,做起来也挺有意思的。史济怀的正文部分写得还是不错的,北大方企勤的书也差不多,不过习题相对更友好一些,配合食用基本上能应付考试了。
- 课程难度:困难
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:中等
- 给分:超好
- 收获:很多
终究还是被奶了一口 这学期数学课无憾了)
(很喜欢老师的讲义风格 遗憾的是没认真听过几节课(因为看讲义就够了) 期末卷子稍微有些奇妙 Stein的部分考得方式有点怪 而且均分很高导致一个失误就被拉分(本人实分析复分析都是这么寄的) 但总体来说是很不错的课程 这学期的容量也让我感受到了一些来自分析的有趣(?
- 课程难度:中等
- 作业多少:中等
- 给分好坏:一般
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:一般
- 收获:很多
等到暑假了做个网站把讲义传上去
也不算是讲义,就是上课老师在黑板上写啥我就在本子上抄啥的笔记。必须得说李老师板书和讲解真的好,有些老师更像是一个引导者,思路只是讲出来并不会写黑板上,下面的同学听着很顺思维一步一步往前走就可以。而如果如此相比,李老师更像是传统意义上的老师,他的板书几乎和思路重合,而且板书上写完一个证明之后如果证明比较长还会再理一理证明的思路。
课本前半部分史济怀,后面讲Fourier级数啥的会用Stein。史济怀的题还是很有意思的,愿意的话可以建个群讨论讨论习题怎么做(可以试试全做,大部分题知识上不会超过本节内容,只是难但不是不能做,但极少部分题目...过程非常曲折和长,或者就超出本节内容,当然也许有不超的做法只是我菜想不到)。
还没出分和调分,分数部分待更。
最后放个小题在这,看看有无大佬能不用复分析知识把它证出来
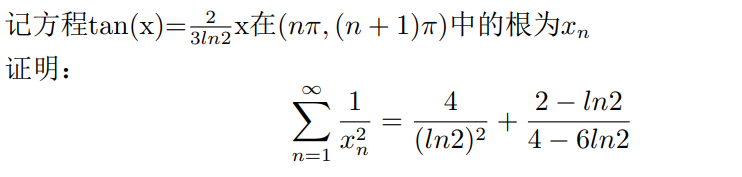
- 课程难度:中等
- 作业多少:中等
- 给分好坏:一般
- 收获大小:一般
- 难度:中等
- 作业:中等
- 给分:一般
- 收获:一般
刚开始的时候不是很喜欢李老师上课的风格,感觉有些东西都会避开,再加上老师上课比较冷漠,感觉气氛有点压抑。而且上课的速度有点快,就忙着记笔记,有的时候经常跟不上。
大概过了一个月,可能突然开窍了?那个时候应该是突然明白过来复分析是一门技巧比较高的课,有些东西违反自己的直观,需要了解一定的定理,例子,掌握一定的技巧。然后重新看复分析就会有另外一个感觉,好像一切都会变得自然起来。之后上李老师的课就会发现老师是讲的很清楚的,或者有些讲不清楚的东西由于课程的限制没有办法讲清楚?定理的证明也会很详细,老师每一次证明完之后就会带着我们重新过一遍思路。慢慢的我就开始喜欢上这个老师的课了。
作业的话,刚开始实在是太困难了,后来手上有了一本方企勤的《复变函数教程》,一切都变好了起来。
考试的话基本上都是原题,感觉考试有点默写大赛的样子,可能是怕我们考的太低了不好看??总之挺迷的。
给分的话,好像老师在卡绩边缘捞了我一下,orz。
- 课程难度:困难
- 作业多少:很多
- 给分好坏:一般
- 收获大小:很多
- 难度:困难
- 作业:很多
- 给分:一般
- 收获:很多
老师上课条理清晰,板书工整,但喜欢刚用湿抹布擦完黑板就直接写,导致同学们看不清板书。另外做笔记的压力还是很大的,有时候两节课证明个大定理要写几面黑板。我有时候早八迟到,就算迟到五分钟,也会一直落在老师后面,补前面笔记。因此听课还是要紧跟老师节奏,下课再探讨细节,尽量别迟到(bushi)。这门课的课程容量非常大,即使是H班,也就才讲到zeta函数的一些性质,stein的第六章还没讲完。自己学完这门课还是觉得有很多复分析知识需要自学补充。
考试以课堂讲述思想为主,一般会有一道作业题。即使老师说“所有人都会满意”,但我还是觉得H班给分还可以再好点,因为我被卡绩了不太满意()
- 课程难度:简单
- 作业多少:很少
- 给分好坏:一般
- 收获大小:一般
- 难度:简单
- 作业:很少
- 给分:一般
- 收获:一般
个人挺喜欢这个老师的,板书写的比较工整详细,和隔壁两门课的老师形成了鲜明的对比。另外这是第一门让我感觉到老师做题水平很高的课,李老师上课的时候补充了很多史济怀课后(不那么好做的)习题,一些奇奇怪怪的思路要是不讲还真的不容易想到。今年参加了阿里巴巴的数学竞赛,恰好考了一道老师上课讲过的题,成了我唯一一道会做的题orz
不过上课讲太多题了导致进度有点慢,再加上有几节课给助教拿来讲习题课了,结果刚开始的时候说要讲gamma函数和傅里叶变换那些最后都没有讲到,挺可惜的。
如果上课好好听了的话,考试确实不难,没有什么超出作业和课堂的东西。但一不小心还是可能翻车的。期中没弄好70都没有;有幸看到了某第一的成绩——好家伙,还没有我高呢i( ‵▽′)ψ
总之考试还是要好好检查啊。
相比之实分析,个人感觉复分析的分析味道更浓一点。在复分析中,我们会切实的对函数的各种大小作估计,像是在零点和极点附近的估计,还有无穷远处的渐进性态等。我想这是有原因的:复分析研究的是“全纯函数”,其性质很好。如我们所知的,全纯函数,必有(比平均值性质更强的)柯西公式,必无穷次可导,必解析,等等。而实分析研究的是可测函数,它很差,这样的函数甚至可以是处处不连续的(迪利克雷函数)。、 但性质越差,说明它需要满足的条件越少,想要做出切实的估计也就不太可能了;而性质越好,满足条件的函数类也相应的越小,才赋予了我们做估计的可能性。
- 课程难度:中等
- 作业多少:很少
- 给分好坏:一般
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:一般
- 收获:很多
给个9分吧,李老师讲的确实还不错,虽然谈不上特别令人印象深刻,但至少在我上过的课里算是质量比较好的了。
至于李老师的给分确实比较emmm,按往年说法是期中和作业不算成绩期末一锤定音,但今年似乎是算了期中和作业,具体比例未知。然而按照最终总评来看他似乎一分也没有调...
不过有一说一,李老师的考试确实是比较讲武德,基础内容居多。把上课讲过的内容和作业过一遍,考试应该是问题不大。
- 课程难度:中等
- 作业多少:中等
- 给分好坏:一般
- 收获大小:一般
- 难度:中等
- 作业:中等
- 给分:一般
- 收获:一般
就我目前所修课程来讲,科大老师大多数字不咋地,但李老师板书相当漂亮。
第一节课老师在黑板上写了这些内容(也是这门课要讲的内容):
复数基础,全纯,导数,多值函数
复积分,Cauchy公式,最大模原理
级数,孤立奇点,辐角原理,Rouche定理
留数定理,定积分计算
全纯开拓,Schwarz对称
Riemann映照,边界对映,Shwarz-Christoffel公式
整函数理论
Fourier变换
Gamma函数,Zeta函数
可惜由于时间不够,最后两条没有讲。
老师讲课非常细致,会有大量的例题,经常把课上讲的例题布置成作业,让我们默写(抄写)答案加深理解(确实有效)。考试也有大量的作业题送分,其余题也不是很难,还是非常体贴的。(虽然我还是翻车了。)
感觉这门课对于技巧的玩弄出神入化,无论是起初的共形映射还是后面的Schwarz引理的应用、积分计算的各种骚操作,都是满满的技巧的气味。
顺便,虽然是H课,但我估算优秀率应该比普通班高不了太多。