2025秋 2024秋 2023秋 2022秋 2021秋 2020秋 2019秋 2018秋 2017秋 2016秋 2015秋 2013秋 2012秋 2011秋 2010秋 2009秋 2008秋 2007秋 2006秋 2005秋 课程号:PHYS5004P01
- 课程难度:困难
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
| 选课类别:基础 | 教学类型:理论课 |
| 课程类别:研究生课程 | 开课单位:近代物理系 |
| 课程层次:本研贯通 | 学分:4.0 |
课程大纲:群论基础,群表示论,SO(3)群,点群,置换群,洛伦兹群,李群,李代数。 教材:自编讲义。 考试形式:开卷。 作业:每次课1到4题。
教学内容
朱界杰老师的《物理学中的群论》课程内容丰富,包括群的基本概念、有限群的线性表示、转动群、点群、置换群、李群和李代数。尽管课程涉及多个复杂的主题,但由于课时有限,导致后半部分内容,例如李群和李代数等主题,几乎是匆忙带过,学生需自学补充细节。
教学水平
朱老师的教学认真负责,上课有条理,讲义内容丰富,各种概念和例子详细。不过,由于课程安排紧凑,部分学生觉得有些晦涩,讲义的可读性差,因此课外需要花费较多时间消化理解。
作业
作业量大且难度较高,是不少学生抱怨的主要原因。课程开始阶段作业相对少,但最后的几周作业量陡然增大。尽管如此,作业对理解课程内容具有一定帮助,做作业还需时间和对例题的实践。
考试及给分
考试内容严格设置,较样卷有一定难度,开卷考试有利于学生现场学习及理解。不过,朱老师的给分慷慨,调分力度大,普遍能提高学生总评。尽管考试题复杂,分数分布显示给分平均,优秀率较高。
学生反馈
学生对课程的意见分化明显,一部分人认为课程进度推动学生压力过大,诸如课程结构失衡等问题频现。部分学生抱怨课程需要一个完整学年而非一个学期完成。另一部分学生认为课程促进了理论与实践结合,尤其是对量子力学有较大帮助。
总结
总体而言,《物理学中的群论》是门对物理专业学生很有价值的课程,给分慷慨,适合有较强学术基础和兴趣的学生选修。然而,由于内容容量大、进度紧张,准备选课的学生需合理安排学习时间,确保理解基础概念,并能自学后续复杂主题。
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:一般
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:一般
我是18秋上的这门课。
首先说,朱老师这门课是很适合,至少对量子力学有一定了解的同学去学习的。对于一个物理系的学生而言,真正遇到群论,大概也是在量子力学和量子场论中。物理上所谓的群论其实在数学上大约属于群表示论的范畴(有时还包括李代数及其表示论)。什么叫表示论呢?群的元素本身是抽象定义的,但物理上经常面对的是量子力学的希尔伯特空间。物理学家比起抽象的群元素,更喜欢和希尔伯特空间上的算符(矩阵 in some sense)打交道,因为它们是更加具体的数学对象,更有可操作性。所以在量子力学之前,不需要认真考虑对群论的学习,因为不太用得上;反之,在量子力学中大家就应该好好考虑补充一些群论的知识了。朱老师这门课大致面向的就是这样的,对量子力学有基本的了解的同学。
朱老师这门课的内容大概包含群的基本概念,到有限群的表示,中间简要讲了空间群和点群,最后简单科普了一下李群和李代数。这对多数同学,其实基本足够了,很多时候物理上应用数学概念就像漫画里的角色在使用技能之前喊出技能名字,都属于只用个定义而已,所以后续内容请根据自己的研究内容决定。
至于给分,应该是科大给分最好的课,大概没有之一了。所以不必操心这方面,考试是开卷的,题目并不难。(朱老师会给样卷,你对着看看就行了)
群论的基本概念没什么好说的,但我建议大家每个概念都记住几个例子,并思考一下这个概念/定理有什么作用?(你觉得没用当然可以直接忘掉)。有限群的表示的部分其实用处不是太大(我不清楚它在计算物理上面会不会更有用),但conceptually simple。对于表示论,请大家好好理解不可约的概念,然后你发现舒尔引理其实就是把它用了一种更为方便的形式表达而已。这部分最重要的结果无非就是不可约表示的正交性及其一系列推论,比如特征标的正交性定理,可以快速帮你求出tensor product representation的直和分解。借助regular representation,我们构造出了有限群的所有不等价不可约表示。不过由于其维数过高,不方便计算。为了简化计算,又有了利用杨图构造表示的方法。
之后的内容我其实已经不太记得了,只记得老师匆忙间科普了拓扑和微分流形,李代数的部分则是简单记了几个结论,比如半单性的cartan判据,dynkin diagram。(不过我觉得这些东西仅从这个课是学不会的,多数同学也没必要去学。)
事实上,真要仔细地学习一遍李群和李代数的理论,尤其是其表示论,是很麻烦的事情,因为它在数学上同时牵扯到分析,几何,代数。例如你要先学习微分流形的理论,具体的构造,例如Haar测度,Peter Weyl定理又得依赖于分析学,对代数的依赖自不必说了。不过有兴趣多去了解一些基本的事实我觉得也是很好的。
如果你想看点角动量之外的例子,不妨试试Weinberg量子场论I的第二章。利用Poincare代数的不可约表示构造单粒子态令人酣畅淋漓,大呼过瘾。我想这应该是一个成熟的理论物理学家对已有理论必要的总结。(正如朗道之于力学,场论)
如果你觉得朱老师讲义的内容满足不了你,比如你想做比较formal的高能理论,经常需要计算比如so(24)李代数的不可约表示,那么我最推荐的方案是去看吴从军老师的note,他的个人主页是https://wucj.physics.ucsd.edu/,他在ucsd讲授群论课多年了,基本上把朱老师的内容全都cover的同时还仔细讲了很多李代数的表示论。(我选课那年因为时间仓促,朱老师讲李代数是用3h开飞车快速讲完的,基本上啥都没学会。)
此外,一些更加细节的东西,你基本上都可以在大黄书(conformal field theory)下册第13章找到,例如branching rule什么的,按需服用。第14章甚至包含了你可能用到的几乎所有关于Kac-Moody代数的内容。
对于做凝聚态的同学,我推荐Dresselhaus的书,有大量实际能带论的例子。(不过我没仔细看过,凝聚态人失格X()
当然还有其他很好的材料,例如gtm222,或者Georgi的,Zee的书,我不太想写书单,所以不列了。
我以前出于对数学的狂热,过分的高估了群论的重要性,现在看来,走了不少弯路。但无论如何,对physicist而言,学习群论最行之有效的方式就是去算。去把它们的表示给explicitly地写出来,去把李代数的data给全都推一遍。你总不能把计算细节留给作者:)
群论为什么物理上如此重要?我先给一个从凝聚态的观点的解释。上世纪60年代,人们惊奇地发现,在临界点附近,物质的微观细节不再决定物质的行为,起决定作用的是,空间维数,以及其对称性。这个现象称为universality,普适性。其实早在普适性被广泛认识到之前,朗道就已经使用了对称破缺的概念来刻画相变了。在这种观点下,抛开空间维数,我们可以放心地说,对称性决定一切。物质的相按它们的对称群进行分类,这就是朗道理论最核心的地方。(当然,这个故事还没讲完,感兴趣的同学可以自行了解)。
祝大家学得开心:)
这门课的情况在21年附近发生了很大的变化,建议大家参考更新的评论,不再推荐大家选这门课。
- 课程难度:困难
- 作业多少:很少
- 给分好坏:一般
- 收获大小:很多
- 难度:困难
- 作业:很少
- 给分:一般
- 收获:很多
什么是迷向张量?转给身边的老人! 迷向张量是怎么一回事?迷向张量是什么梗?迷向张量最近为什么这么火呢? 说到迷向张量大家肯定都不陌生,但是你知道迷向张量到底是什么吗?相信大家对迷向张量都很熟悉,迷向张量就是我们每天都会经常遇到的,但是迷向张量是怎么回事呢?今天小编就带大家来看看究竟是怎么一回事。 迷向张量其实就是迷向张量,目前在网上拥有非常高的热度。大家可能会感到很惊讶,迷向张量为什么是这样的?迷向张量究竟为什么火起来了呢?但事实就是这样,小编也感到非常惊讶。 以上就是小编为大家带来的的关于迷向张量是什么意思,迷向张量是什么梗的内容。如果大家喜欢,可以点赞表示对小编的支持。欢迎在下方评论和小编一起讨论喔
- 课程难度:简单
- 作业多少:很多
- 给分好坏:超好
- 收获大小:没有
- 难度:简单
- 作业:很多
- 给分:超好
- 收获:没有
讲的烂不是你的错,自己脑子有病还开课出来祸害人就有问题了吧
这是我上科大以来见过教学质量最差的一堂课,前期把环域等课程无关的东西嗯塞一通,一个概念要讲三四个例子,后期在四周内讲完一半内容。给你的十七个教学周都让狗吃了?我不备课想到啥讲啥都讲不出这水平。很难相信这是一个开过很多年的课。不仅讲的烂还留大量作业恶心人,本来连着几周作业挺少的还想夸两句。结果进了最后四周又开始一节课留四道题每道题四个问。授课教师难道觉得同学们和他一样可以不在这门课上投入任何时间?不想教人可以不开课,还想吃空饷可以不留作业。
授课教师脑子有问题1分起评,作业多-2,给分好+1,总评给不了0所以给1了
调分公式:作业分=min{作业平均分/82.35 1,1} 总评=卷面+(100-卷面) 作业分*0.39
82.35好像是班级作业平均分,0.39是待定调分因子,今年卷出简单了所以比较小
推荐人群:能看懂讲义且爱写作业的或能找到爱写作业的同学抱大腿的。下面有人把作业答案发出来了,不过不出意外的话朱姐姐会换题的。
23秋期末:
1.写出所有2024阶Abel群
2.[51]杨图杨表U((1,2))标准表示
3.两个自旋1/2耦合,写出总自旋1的自旋波函数
4.四面体置换群求共轭类、给定四维表示求特征标、不可约表示数量及重复度(感觉这里有typo,想问维数才对。因为下一问问的也是重复度),这个四维表示中单位表示重复度,高维(指大于1)表示的特征标
5.求保n个粒子升降算符对易关系的变换矩阵,直接写出李群维数、是否紧致、连通度
6.xp对易子相关的李代数问题,求结构常数、killing form、中心等东西。求海森堡群不变测度
7.套皮循环群的三维线性方程组有解判断并求解
- 课程难度:困难
- 作业多少:很多
- 给分好坏:超好
- 收获大小:一般
- 难度:困难
- 作业:很多
- 给分:超好
- 收获:一般
科大生存法则之一:你不缺学分,不要轻易选不必要的课。想学知识,哪怕旁听呢,花不了多少时间精力。
大三秋季学期选课,上到一半跑路了,实在受不了了。我无法理解为什么我要花一晚上去数珠子的排列有几种花色。对于一个同时在学量子场论、学量子场论课(和前者并不是一件事)、为了参与课题而恶补宇宙学但其实广相都没接触过、一个月后考T、四级大雾实验几乎一动没动、有着各种各样必修且与专业无关的课、本身又对群论毫无“感觉”的人,这门课真的是折磨。
群论确实很重要,群表示论在物理中甚至更重要,但是个人观点,知识、认知都是循序渐进发展的,所以看到weinberg用群表示论构造单粒子态(ch2)和相互作用的场算符(ch5)时,会觉得很自然,但是面对一大堆特征标、生成元、CG系数的时候,看不到任何的物理。
建议后来人旁听一部分,选课需谨慎…… (惨痛教训就是两次退课全都花在了“群论”上(近世代数和这个),群论属实一生之敌…)
以及作业,又难量又多,真的unbengable…
- 课程难度:中等
- 作业多少:很多
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很多
- 给分:超好
- 收获:很多
化院大二。今年两百多人选(课程群有两百五十多人),选课的本科生八十多个,占快一半,大二应该只有我和另外两位物院同学。
朱姐姐的讲课水平不用说了吧,给分也是出了名的好。答疑也很有耐心,提前二十分钟上课,每次下课后都会被同学纠缠到快十一点2333
课程内容上,今年简单介绍了一下洛伦兹群,所以这门课内容看上去比较多,但是很多部分都是简单带过,只做介绍。感觉学群论是目前来科大收获最多,花了最多心思的一件事。今年作业还是挺多的,31次课,留了27次作业,每次大概1~3题不等。学起来的困难主要是需要线性代数,量子力学和张量的基础。
听说北大的物理口群论课分两个学期,前面讲有限后面讲李群,感觉这样做两边都能讲的比较细致,不知道老师能否参考一下(?
- 课程难度:困难
- 作业多少:很多
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:很多
- 给分:超好
- 收获:很多
这门课的作业非常多,上面的文件里是我这个学期手动整理的一份作业答案,仅供参考。同时在老师要求下,我在这份答案里偷偷添加了部分错误,还望同学们不要直接抄答案。下面是对这门课的总结:
课程内容
第一章、群基本概念
群的定义、性质;子群、共轭类、商群;同构、同态;置换群基本介绍;群的分类
第二章、群表示论
线性表示理论、幺正表示、真实表示、共轭表示、对偶表示等;表示的等价性、可约表示、正则表示;群函数、群函数空间、群空间、群代数;寻找所有不等价不可约表示;特征标理论、类算符、投影算符;Abel群与非Abel群的不可约表示;分导表示和诱导表示;李群的表示。
第三章、转动群
转动矩阵、转动群SO(3)的定义;SO(3)指数化与伴随表示;角位移参数化和欧拉角参数化;SO(3)群的覆盖群SU(2)的定义;SO(3)和SU(2)的同态关系;李群的不变积分、Haar测度;SO(3)和SU(2)的线性表示、D函数,球谐函数;so(3)和su(2)李代数、无穷小生成元、李氏三定律;李代数的不可约表示、升降算符和Casimir算子;直积表示的约化、角动量耦合理论、CG系数;Wigner-Eckard定理
第四章、点群
这章没讲两节课,就是证明了晶体点群的制约定理,然后给出了230种空间群,再对点群按照晶系进行分类等等
第五章、置换群
置换群的基本概念(第一章);置换群的轮换结构与配分数;杨图;杨表、正则杨表;行算符、列算符、杨算符;杨算符投影出置换群不可约表示、钩型数;置换群生成元的不可约表示(填充法);置换群特征标表的正则填充法
第六章、李群(开始起飞)
拓扑学的基本概念、拓扑空间;流形、连通性、紧致性、连通度;微分流形和李群、李群的性质;常见李群;李群和李代数:李氏三定律;伴随表示
第七章、李代数(飞得更快)
李代数的概念、同构、同态;子代数、理想、中心;单李代数、半单李代数;Killing-Form;Casimir算符;可解李代数和幂零李代数;Cardan子代数和根矢;根图、Dykin图、Cardan矩阵
考试题目
今年也是很精准的预测到了T群的考察,下面是今年考察内容:
1. 群的分类定理:问2024阶Abel群有哪些?
2. 杨图杨表杨算符的三连问,正则填充法
3. 角动量耦合定理:直积态的约化、单重态和三重态
4. T群(A_4群)表示的六连问:共轭类、特征标、可约性、不可约特征标
5. Sp群表示矩阵需要满足的条件、李群维度、连通度、紧致性
6. 海森堡代数:结构常数、Killing型、不变测度
7. 套皮李代数的本征问题求解:零空间、特征值、特征矢、特征空间
下面附一下我考前对考题的预测,基本上能涵盖这门课能考到的东西(后人可补充),今年也是预测到了T群的考察:物理学中的群论_2023秋_考题预测.pdf
考试成绩
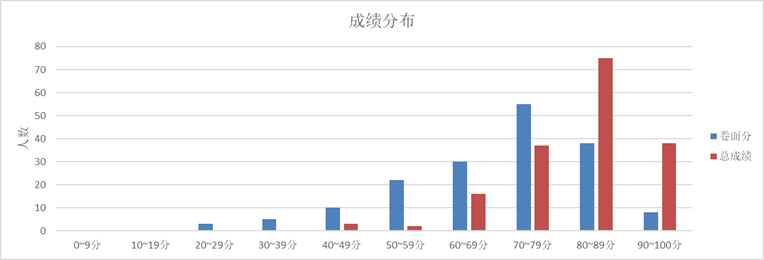
本人是被捞到90+了,感谢姐姐和助教的一路陪伴,这门课确实能学到非常非常多的东西,难点在于作业非常多(我发的答案仅供参考),考试难度也有,但最后成绩都很高,适合学有余力的同学来选群论。下面是2023年秋的全班成绩分布
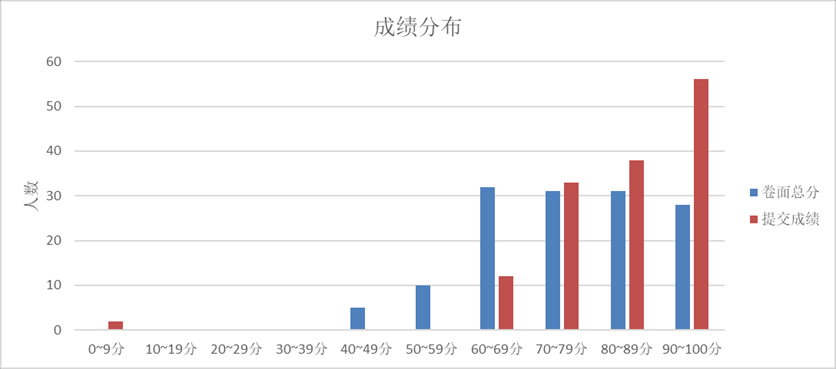
求求大伙点个赞再走吧(T_T)
- 课程难度:中等
- 作业多少:很多
- 给分好坏:一般
- 收获大小:一般
- 难度:中等
- 作业:很多
- 给分:一般
- 收获:一般
一言难尽的助教和一言难尽的课
能看出来老师是认真备了课,讲课水平算是不好不坏。这次主要是来点评一下这门课2023年秋季学期的助教,真的是非常奇怪的一个人。
首先就是助教一直有一种 ”我花了时间给你们批作业,快看我多么辛苦,快感谢我。“的奇怪感觉。这么多年,一个劲在群里强调自己 “做了一天群论。”,“批了一整个晚上。” 的助教,我真的是第一次见。因为科大的大班有很多,既然选择了当助教,其他助教都把花几个小时批作业认为是自己应该做的理所应当的事,而不是像群论助教一样自我感动。
下一个奇怪的点,就是这位助教似乎没有搞清楚,他当的是助教而不是我们的导师,对我们进行人生教育并不属于他的职权。因为很多同学第一次用BB系统,提交作业时出现了疏漏,在询问助教补救措施时,助教的第一反应是阴阳怪气:“不管是企业还是高校,在这种小事上犯错是会被干的。”,恍惚间我还以为是老板在对我进行训话。
而最迷惑的点,就是有一次因为助教表述不清导致几个同学错过了交作业的时间,因为是助教的疏漏导致的漏交,他们在群里询问助教解决方法想进行补交。但是助教始终避而不谈,拒绝承认是自己的疏忽,甚至告诉他们 “每次作业只有0.3,根本伤不到你。”。感觉已经不是 “奇葩” 可以一言以蔽之了。
希望老师下个学期能多招两个助教,至少能中和一下奇葩程度。
二编
收回那句老师认真备了课的话。从国庆节以后,就开始把每节课的时间提前到七点十分,有时候还会拖堂,就算是这样,还是把大量的内容挤压在最后几周放飞自我。真的难绷。说实话,科大拖堂或者额外加课的老师不少,但是有些老师加课以后是真的能够非常高质量地完成教学内容的,是让人感觉学到了非常多的东西,而不是像这门课一样,感觉填鸭一样塞了很多东西,但是什么都没学会。开始质疑老师的课程安排。
而且助教为什么要把群当朋友圈发呢?学校开什么晚会和我们的教学任务没关系吧?就非要半夜批作业然后凌晨四点在群里发:“当你们还在睡觉的时候我作业已经批完了”,然后等着群里同学发“助教辛苦”,说实话,真的尬得鞋都抠烂了。
三编
考完试了。考试卷子的难度和样卷差了一个东非大裂谷,寄。
助教您看得开心就好,还写了这么多担心您看不到呢。
- 课程难度:困难
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:很少
- 给分:超好
- 收获:很多
(冒着牺牲自己绩点的危险为后人收集信息。。。发现自己很伟大)
首先我讲一下这门课的课程内容难度。第一章,群论基础(就是讲一些群的基本概念,基本上跟数学专业的那个近世代数里面讲的群的概念一样)第二章,群的线性表示理论(就是讲用矩阵表示群,这一章的难度比第一章提升了一个档次,这一章的概念很重要,不可约表示等等)第三章,转动群(这一章跟量子力学的关系挺大的,当然我听到这一章已经完全听不懂了。。。这一章的东西很复杂,不变积分,紧致群,李群李代数,无穷小生成元我完全懵逼了)前三章是一个学期的重点,大概讲到11月份下旬的样子,开始后面的“大跃进”讲课。。。第四章,点群简介(真的是“简介”,我还没来得及理解就讲完了,而且就讲了一节课)第五章,置换群(这个讲的也是很简略,但是挺重要的),第六章,李群(上来就是拓扑学简介。。。)第七章,李代数(这个跟第三章有关系,而且这章都是最后赶进度赶掉的所以非常快。。。)
总之,知识真的是强行被灌到脑子里的。。。而且课后要花时间琢磨和复习,不然下次听课一脸茫然。。。
但是,这门课学了对以后的课程学习很有帮助!(我也说不出具体有什么学术上的帮助)。作为本科生,我学起来很吃力,我也看到我的同学接二连三的退课。。。(开始的时候我认识有将近10几个选这个课的我认识的本科生,最后我认识的还剩下不到5个,这个退课率可想而知。。)但是你坚持下来了你的感觉会跟别人不一样!还有,朱界杰老师真的人特别nice,特别负责任,平时下课可以缠着他问问题,课后发邮件也可以。考试之前他会亲自过来答疑,考试完了他还会发邮件给每个同学他们的卷面分,小题分,总评什么的(总评肯定比卷面高了很多。。。)
总之,选了这门课,你只要坚持下来了,考试之前认真复习了,最终你知识上和抗压能力上都会得到提高,而且最后的给分也不会辜负你的付出!
PS:考试题目肯定会考一个证明是群的题,一个邓金图的题,一个置换群杨图杨表杨算符的题,还有一个一定是李代数的计算题(无穷小生成元,对易关系等等)。考试之前有样卷,一定要好好琢磨。一共考五道题
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:一般
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:一般
叹气。
这课的讲义写的不行,看不懂,不如数学系的书逐本看看。而且因为缺乏严格的论述,会让人误用定理,错误理解定理,需要看数学书,或者写的比较正规的物理学群论书。
上课内容可以不听,证明多是用矩阵技巧而不是空间,学会计算是主基调。
助教是个把课程群当qq空间发的有趣的人。
这课不是给理论物理开的,所以指望优美的理论请自学,不要打扰研究生学习工作知识。
因为学生基础不好,所以这么群论从最基本的代数学基础讲起,而不是直接突入群表示论。
如果希望学李群李代数的话,可以出门从数院王🚀的微分流形开始,从微分流形学起可能学的更清晰一点。
这门课一定是导论课,只有导论课会这么备课。
带助教的同学下次一定要说清楚补交到底是怎么情况,不要一边嘴上说过了期限不收,又在群里说我还没改快点交呀。
叹气。
想正经学数学还是去数学系听课吧。虽然训练数学家的方式与物理学家不同,但是训练凝聚态、原分、光学、理论物理、等离子体物理等等的学生差异更大,想正经学数学想来是对理论有追求的,理论物理与数学的差异可能比上述差异要小一点。
叹气。
有限群的表示论可以参考《群的表示和特征标》的前一半,关于不变积分测度和拓扑学的理解可以参考丘维声的《群表示论》,至于剩下的东西都去参考物理学的群论书罢。
如果想要看群论和量子力学的联系的话,外尔作为首个将李群表示论运用于量子力学的人,其所写群论与量子力学可以一看(不过符号与国内符号不一致,翻译的水准更是一言难尽)。如果是量子场论的话,想来运用群论观点颇多,无需赘述。
讲得最好的是转动群和基础知识,这部分可堪一听。
转动群里的EW定理的一个优雅论述可以在科恩的量子力学第二卷角动量一章的补充材料中找到。
md,矩阵论果然是让人觉得恶心的东西。虽然有时候矩阵论更简洁但这不妨碍我看到一堆角标和打洞和找基矢就想杀人。
这助教怎么李群李代数都不会?他真的会微分流形吗?
我戳了,矩阵论没有什么时候是简洁的。不管是哪个定理都可以用空间写。
————————
超,把A4的类都算错了我还以为似了,结果还能86,这给分真神仙吧。
- 课程难度:中等
- 作业多少:很多
- 给分好坏:超好
- 收获大小:没有
- 难度:中等
- 作业:很多
- 给分:超好
- 收获:没有
授课和讲义不像一个有任何数学素养的人干出来的事,越上感觉离好数学越发遥远。作业题目都讲不清楚,几乎没有启发意义。想学代数去陈小5近世代数打个基础,看看Artin的Algebra基本这门答辩课就不需要了。完全不推荐。
另外,zjj的理力除了作业题有些恶心,给我打下了很扎实的基础,那门课还是很推荐的(2024..7.16看来,这点需要打一个大大的问号,even 一个大大的×)。
另外改卷子的人不懂有限生成abel群怎么分类,把对的(Smith标准型整除链的写法)改成错的我毫不意外,毕竟助教不太懂,老师上课讲的也不全是对的
- 课程难度:困难
- 作业多少:很多
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:很多
- 给分:超好
- 收获:很多
万人血书(1/10000)求朱姐姐把群论开成两学期,李群李代数最后三节课讲完,李代数就讲了一节课,出一道李代数大题o(╥﹏╥)o
期末共七道大题:
一、SO3群的自身表示是否可约(作业题)
二、证明Mobius变换(给出了表达式)是群同态,并求出同态核(朱姐姐说的送分题)
三、置换群S5 画出[41]的标准杨表、写出标准表示(朱姐姐说的另一个送分题)
四、n个1/2自旋场耦合n阶张量场(n个SU2直积)的特征标、n/2自旋部分(Dn/2)的重复度、该n阶张量场中全对称部分的独立个数(维数)
五、2022阶有限Abel群共有几种
六、D6群的展示、共轭类、Burnside定理、一维不可约表示、特征标表和投影算符
七、基于理论力学的李代数七连问
但是给分是真的好,卷面80总评91,也许只有我能脑抽到把杨图的行列搞反,本学期仅一人未参加期末考试而挂科,以下是成绩分布
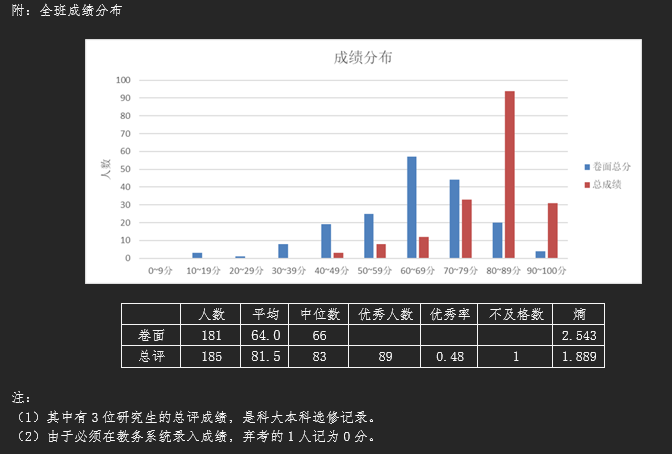
- 课程难度:困难
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:很少
- 给分:超好
- 收获:很多
物理学院大二本科生,我的评论难免会有按本科课程来要求研究生课程的成分。
虽然我给的不是满分10分,但我还是十分推荐这门课的,因为值得。
这篇评课做的主要是说为什么少了一分。
我扣一分不是因为我没学过量子力学就来听感觉吃了——这是我自己的事,毕竟其他同学大多有扎实的量子力学功底(不过如果要听懂洛伦兹群那章可能得会量子场论)。
对于本科生而言,期待的课程是有详细的讲解和说明的,作为雾里人,可能有时不需要严格证明,但多少不能合理性简介也不说直接上来就抛一个概念。这门课前三章老师还是讲得非常详细的,但5~8章就是开快车讲了。章节分别是抽象群论、群的线性表示论、转动群、点群、置换群、洛伦兹群、李群、李代数。这门课应该是两个学期的量,被压到一个学期了,结果就是置换群直接告诉你怎么填杨图杨表、洛伦兹群一个半小时讲完、李群只讲了比数学分析难一点的微分几何、李代数相当于是对着PPT读(前六章都不用PPT,后面赶进度)。
本科课程似乎要求掌握得比较全面,但研究生课似乎各有所爱了。比如老师上课时也时常说”有些同学可能觉得二自己的专业方向不需要学这么多“。有限群的线性表示论为例,老师讲得比较深入,当中一些做法比较通解了,考试时……会正交关系就差不多了。个人觉得李代数部分蜻蜓点水带过实在极为可惜。
至于考试——没有作业难,但比样卷难不少,做好样卷保期末考卷面及格,作业如果融会贯通保卷面95。(以及今年朱老师没考邓金图……)
这门课感觉还是适合大二、大三同学选的。
量子力学基础差问题不是很大,需要补的主要是角动量理论那part……但如果还没学线性代数就算了。
至于教材,我预习时看的是马中骐的,不推荐。老师的内容不少于韩其智、孙洪洲的书的影子。如果要找中文书的话,可以去图书馆看那些有点年代感的书。
出分后补充(9分评价是出分前的给定的,不受给分影响)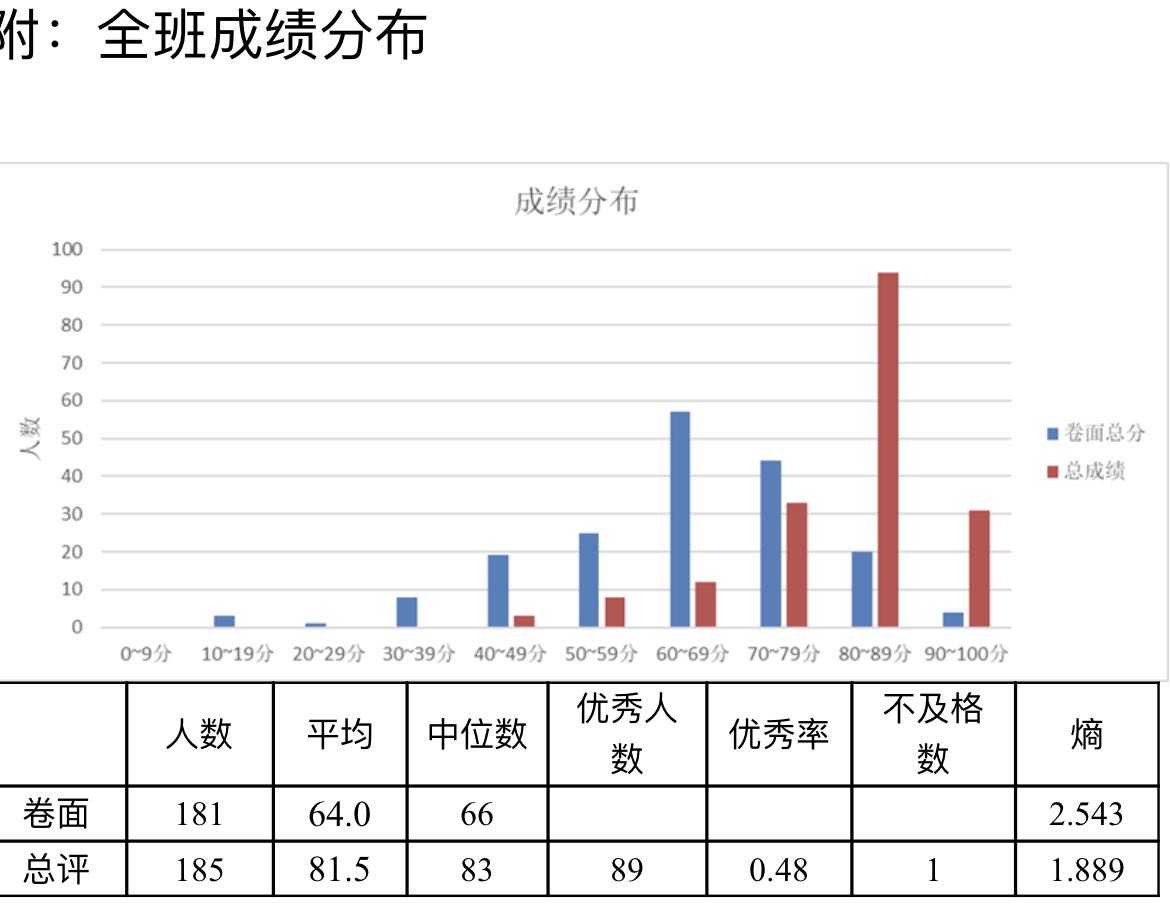 2021~2022秋季学期成绩
2021~2022秋季学期成绩
本人没学过量子力学就头铁选了,感觉卷面分也挺不错的(当然,直接作为总评还是低了点)。优秀率对本科生来说挺高的了,及格嘛,去考试就好。4.3的话……可能还是得全班前十吧……
- 课程难度:困难
- 作业多少:很多
- 给分好坏:一般
- 收获大小:一般
- 难度:困难
- 作业:很多
- 给分:一般
- 收获:一般
作业多,作业难,讲义写得不好,没用的内容也多(对于高能),容量也过大,选课人还巨多,直接失去听课体验,这学期算是被这门课单杀了,耗费了巨量的时间,群论收获最大的地方却在Weinberg量子场论和srednicki量子场论。出分再追评。
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:很多
这门课加到本科生的选课列表里了, 谈谈自己上过的感受.
首先是内容, 课程内容从字面看上去很多, 群论基础, 离散群的表示, 转动群, 置换群, 点群以及后面的李群李代数初步, 但是实际上完一学期课再回头看其实也没多少东西. 这门课的大部分时间都花在了群论基础, 离散群的表示以及转动群上, 前两个主要就是介绍并证明一些主要的定理结论, 而转动群主要通过SO(3)和SU(2)的表示带你看一看处理李群的基本思路, 并且让你对李代数产生一个很naive的感觉. 至于真正有用的李群李代数, 只是起了一个头, 这无可厚非因为课时有限, 如果对这个有需求的童鞋可以去超星找梁灿彬老师的课或者自己看朱老师给的参考书. 这门课上老师会提很多和场论等等有关的群, 给大家扩展知识面.
我大四上学期蹭过半学期这个课, 研一完整上过一遍. 第二遍听的时候整门课的理解我没有感觉到困难, 上课方式是纯板书, 朱界杰老师的讲课水平不需要我说大家应该都了解, 所有东西都有条不紊, 十分清晰. 期末考试十分和谐, 平时讲的难期末考试全是白送分的题而且开卷.
个人感觉很适合物院大三来选(其实这个时间点学群论对于某些人来说可能还是有些迟了), 虽然这是一门研究生课. 转动群那一章会把角动量耦合, CG系数以及Wigner-Eckhardt定理(不确定拼没拼错)都讲了, 这些对于学量子力学时候轨道角动量的理解有极大的帮助(那个学期物院正好在开量子力学).
因为这门课是研究生课, 没有助教, 所以没有作业, 老师只会布置一些题, 做不做都无所谓
- 课程难度:困难
- 作业多少:中等
- 给分好坏:超好
- 收获大小:一般
- 难度:困难
- 作业:中等
- 给分:超好
- 收获:一般
我说以后要在质数-1年秋选课有没有懂的
- 课程难度:中等
- 作业多少:很多
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很多
- 给分:超好
- 收获:很多
1.这门课还是有一些不太合理的地方的。首先是这门课内容实在是远超四个学分的量,到了十月份了就经常提前上课延后下课。其次是这门课助教只有一人而学生有一百多人,所以助教要做的事情自然太多了,使得有效的作业反馈完全不可能。虽然有这两个问题但还是瑕不掩瑜。
2.老师安排的内容非常全面,讲的也非常直观而细致,让我绝大多时候都听的兴趣盎然。课程正好弥补了我之前学习的空缺,之前的论文中的看不懂的推导和记号,现在也能大概知道是怎么回事。
3.作业虽然每次课后都会布置,但是题量也不算大半个小时就能做完。考试虽然内容虽然比较多但是形式是开卷所以有些地方现学也来得及。我写了一份回忆的试卷但是为了尊重老师不打算放上去了。最后调分力度也很大,虽然这次我卷面也满分了所以对我用处不大,但是当年理论力学考的一般的时候真的救了我一命好吧…
- 课程难度:困难
- 作业多少:很多
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:很多
- 给分:超好
- 收获:很多
一门课程,不是因为他讲的内容重要,最后给分好,就能被称为一门好课的。课程分数严重虚高,必须向下拉一拉。
这门课最大的问题已经被广泛讨论了,即课程结构严重失衡,在提前上课的情况下,最后两周依旧直接起飞。据其他人反应,zjj其他课也一贯起飞,可见他根本不善于安排详略。做一个未必恰当的比喻,就像一份营业价值很高的食材,用最恶心的方法烹饪,能成为一道好菜吗?
另一个令人不适的地方是这门课上疑似富集了物院里构成柯南刻板印象的一类主力人群,导致这门课的氛围比较明显的异于一般专业课或研究生课,也令人难以服用。
- 课程难度:简单
- 作业多少:很少
- 给分好坏:超好
- 收获大小:一般
- 难度:简单
- 作业:很少
- 给分:超好
- 收获:一般
虽然已经毕业了, 见到有人讨论就来评一下.
这个课在2021秋开始作业需要上交, 此前因为没有助教所以作业不收不改, 约等于没作业. 于是这个课的风评在那个学期之后开始变差
不限于这个课, 也包括他的理论力学, 朱老师对教学内容, 尤其是数学部分, 的要求, 颇有一种贪多求全的感觉. 而他对课程进度的安排一直也是灾难性的, 往往是前面的内容大讲特讲, 务求全面覆盖, 事无巨细. 到最后一个月就开始光速赶进度. 这样的结果就是, 这门课的讲义的前一半有一种曾谨言的风格, 各章相互平行, 内容详细, 可当字典查阅; 而后一半就是完全没有可读性的大纲.
在没有作业的年代, 这个课因为没作业, 考试简单, 给分好, 并且和量子力学有关的转动群部分讲得详细而饱受本科生好评, 这是非常符合妮可一般规律的. 但在作业多而且很古怪的情况下, 风评出现变化也不足为奇了.
个人推荐学群论还是读A.Zee的书, 虽然厚但是可读性很强. 这本书在未来的几年内可能会被翻译出版, 敬请期待.
此外, 对于没打算做偏理论的方向的同学学习群论, 我是很怀疑其必要性的.我学了之后就几乎没有使用过, 除了在学习另一些我同样用不上的数学的时候. 但群论确实是物理背景的同学接触代数的最佳的窗口, 而代数的思想多少会改变人的思维方式, 所以把它看成像普物那样的思想政治课或许也不错.正如普物的目的是让你习惯物理学家的思维方式, 熟悉物理学家社群的黑话一样, 群论能或多或少地让你了解一点理论物理学家的思维方式. 但这样的训练能不能在这门课中达成呢?我不好说
我为什么要选这门课喵?
为什么要在1月23号晚上考试喵?
周围人早都放假回家了,玩上终末地了喵…
我一个人对着看不懂一点的ppt欲哭无泪喵
😭😭😭
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:很多
给姐姐拉个分。不知道为什么大家怨气这么重,但是还是支持姐姐。注意这门课的目的是面向大多数各个方向的同学,为大家打群论的基础。如果你对某个方向感兴趣,可以自己去看书。既然是为了打基础,老师在前半部分讲的慢些也是正常的,符合教学目的的。至于部分怨气深重的同学,觉得老师后半部分讲的快就是没有好好备课,烦请您了解一下这门课的教学目的。老师开始就说过,对于班上大部分没有基础的同学,入门太快,基础不牢带来的问题远远大于最后讲的快一些的,因为有了基础概念的掌握,后面的部分各位还可以自学。其次,老师没有夸张到四周讲完一半内容的。后面的部分老师主要是讲一些基本内容和框架,没有追究很艰深的内容,是为了让你无痛入门,为以后进一步学习打基础。老师不管是作业还是考试都没有在后半部分难为大家。最后,老师给分还是一如既往的超好。(评论区的部分怨气深重的懂王也在出分后表示真香)。
- 课程难度:困难
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:中等
- 给分:超好
- 收获:很多
好难好难好难,要学哭了
内容真的多 前面学了忘 忘了学
学着学着会来怀疑 我学习的目的究竟是什么
学物理是为了什么
人生的意义是什么
但是我个人非常喜欢老师上的课,我对内容安排没什么意见,老师的课在课堂听确实很快很头疼,但是听录课的时候就还好
作业是真的多,哪怕我大四了其实没多少课写得还是很吃力
整体下来的知识是成体系的,很多量子力学里我本来蒙蒙的地方现在都清晰了很多
助教怎么样我个人是真的无所谓,因为我不听习题课也不管作业反馈,只要能让我把作业交上去就是好助教
很多概念都是第一次接触,学的时候是真的不理解,非常痛苦,但是期末的时候反而感觉豁然开朗了。
出成绩追评
据说优秀率一共给了55%,50多个人90+
老师确实奶人很有一手
- 课程难度:困难
- 作业多少:很多
- 给分好坏:超好
- 收获大小:一般
- 难度:困难
- 作业:很多
- 给分:超好
- 收获:一般
先给9分(截至本人此篇评课时的平均分)避免造成不必要的影响。
晚课又热又困,作业又多又难。
讲义内容丰富,但是可读性堪忧。
本人已经摆烂,准备读读树桑note算了(话说只是读树桑note的话选课干什么,果然非必要不选课啊)
树桑note用来搭建基本的框架,了解简单的应用应该是够的,用来对付姐姐作业则明显不足,不知道以树桑note为基础会不会被姐姐考试薄纱,祝(我)好(运)。(为什么要加上祝好?因为信春哥得永生!)
更新:
绷,寄,麻。
听说往年只要去考试了就不会挂,希望我不要创造历史。
寄。。。
明年还来!希望明年讲义可读性能高一点,作业能少一点,考试能简单一点(好像是在做梦)
不完全寄,被奶了一口。
从总评看确实考试的都没挂,而且给分算得上慷慨,也不是不能选。
样卷和考试试卷不能说完全不一样,但是除了两个送分题(2024阶abel群&杨图)外确实也没啥参考价值。
自己看看书,作业找大佬抱大腿抄抄,然后考前通读一遍讲义,总评上4确实不难。
课的话不建议选课,个人认为也没什么完全听一遍的必要,转动群部分挺好,有兴趣的可以听听这一部分,基础知识部分也不错,但是一来那时候班级人多抢座位困难,二来这一块找点书和讲义看看效果也差不多。别的就更没必要听了(毕竟你也不会认为可以通过旁听几节课上速成李群李代数吧?)。
更新一下,修改给分为超好(确实超好)评分下调为7分(本学期所有评课的均分向上取整)
确实很难给什么好评,课程内容安排多少有点问题,讲义令人懵古,作业谔谔。
推荐一下知乎🌳桑のNote和朱洪元老师的书《群论与量子力学中的对称性》,当然这只是针对学习; 想混高分(4+)需要找个大佬抱大腿抄作业。
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:很多
超级棒的课程!学到了很多东西!!
这门课程就是为了物理学院的同学准备的。上半学期几乎都在讲理论,比较偏数学。后半学期偏应用一些,会讲转动群、晶体点群、置换群、洛伦兹群、李代数和李群。考试不考证明,只考计算。
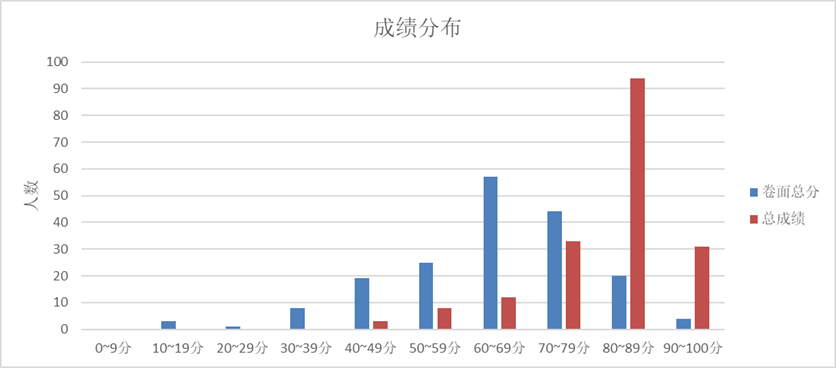
给分很好!推荐物理口学有余力的同学选课。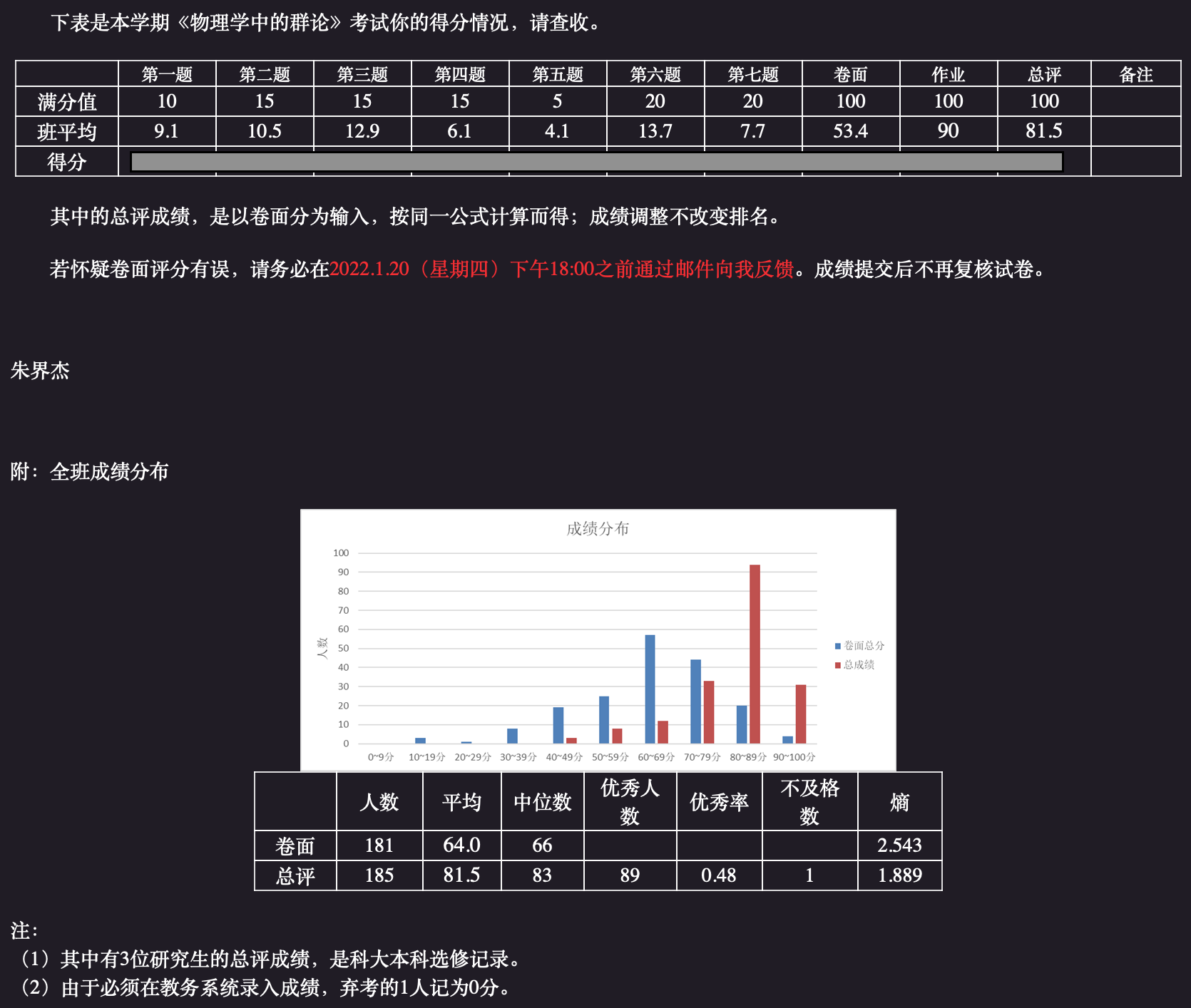
- 课程难度:困难
- 作业多少:很少
- 给分好坏:超好
- 收获大小:一般
- 难度:困难
- 作业:很少
- 给分:超好
- 收获:一般
课程时间有限而内容庞杂,决定了很大一部分内容都是走马观花,要想深入理解,需要在课下下不少功夫,感觉学了一个学期提升比较有限,遗留了很多问题没有搞清楚。朱老师的讲义在某种意义上来说更接近群论某些技术的使用说明书,考试是开卷的,所以就像作实验一样,学期中学习理论知识(很多要靠自学),考试前一段时间了解一下实验的原理,试一试仪器,考试的时候就按着说明书操作。本来是感觉这个课没必要选,自学问题也不大,奈何朱老师堪称gpa之母,给分非常非常好,特别适合大二同学挽救自己被概统和复变暴击的gpa,所以。。。
楼上说的迷向张量是zjj的彩蛋,是样卷上的题平时没有讲过,答疑的时候去问才讲,所以大家几乎都翻车了2333
- 课程难度:困难
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:很少
- 给分:超好
- 收获:很多
这门课真的太棒了!属于收获很多给分又好的课程!
先说收获:这门课先讲群论基础(基本上是有限群的介绍),然后讲群的线性表示,再讲转动群(转动群在量子力学里面真的太重要的,感觉和量子力学里面的角动量理论能完美地结合在一起)然后是晶体点群,置换群的表示,李群李代数。朱老师上课清晰简练,是我在科大遇到的少有的超有条理的老师,真的有超级深厚的数学物理功底!但是由于中科大教务处向来naocan,课时太紧了,一周只上两次课,对于这门研究生课来说真的完全不过瘾,朱老师每次都讲得难以自拔拖堂很久(我也很喜欢听啊哈哈哈哈)建议这门课改成6个学分,或者直接拆成两个学期,前半段学期的内容讲得很好,但后半学期的内容因为课时太紧讲得很粗略,啊!真的非常想听朱老讲李群和李代数,甚至李超代数啊!而且朱老师还超级有耐心,答疑什么的都会整理成文件放到网上,超级nice的老师!虽然很多细节没有补充,但总的来说框架还是搭起来了,后面的造诣就看自己了。
再说给分:我觉得可以当得上GPA之父的给分了,考试开卷,难度不高,平时认真听课复习肯定没问题,作业最好有时间做一下。我这一届有160个人选这门课(加上研究生),根据本人的卷面分数以及本人的总评估计给了十来个4.3,优秀率给到50%(超级棒!)
什么时候科大才能多一些这样无比适合物理学院学生的数学课呢?但提醒一句,如果是想水学分的还是别选了,估计你到第二章就听不懂,又不肯用心好好花时间,到期末肯定啥都不会,虽然给分很好,也救不了那些不用心上课不用心复习的人。
- 课程难度:困难
- 作业多少:很多
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:很多
- 给分:超好
- 收获:很多
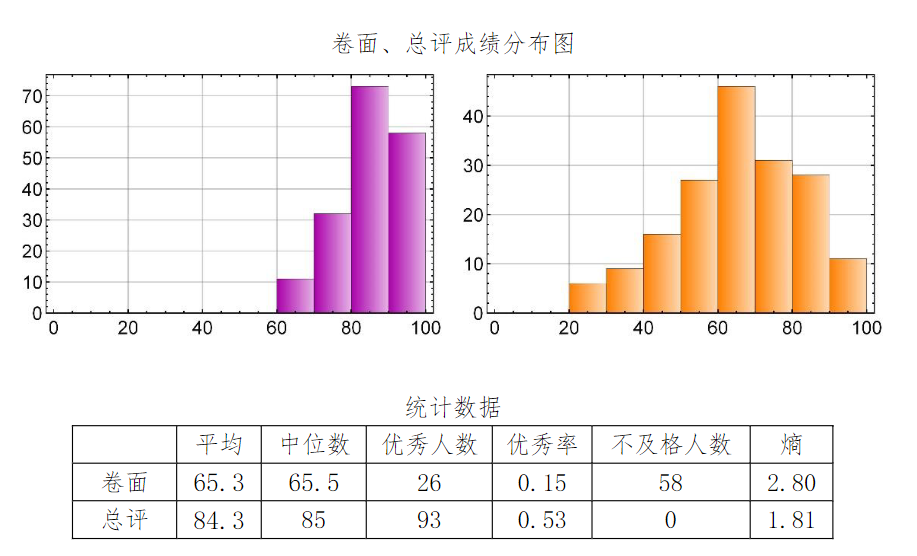
《成绩图》
一目了然,不言而喻
- 课程难度:困难
- 作业多少:很多
- 给分好坏:超好
- 收获大小:一般
- 难度:困难
- 作业:很多
- 给分:超好
- 收获:一般
第三章讲义第23页的su2群不变积分、欧拉角、角位移参数不变积分这几块,生动地展现了当代中文教材普遍的两大问题:
1,缺少通顺的文字叙述,教材本身不像一位循循善诱的老师,反而像是喜欢说拗口文言文的老古董,只喜欢罗列符号计算,完全不符合正常人的阅读规律
2,例题和定理脱节,例题的计算方案和前面讲的东西不一致,甚至在上课的时候亲耳听见老师讲完普遍的定理,开始套上角位移参数做具体计算的时候,说:“这里实际上是……所以我们就可以不用这么计算了,而是去计算……”,徒增学习成本
- 课程难度:困难
- 作业多少:很多
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:很多
- 给分:超好
- 收获:很多
原来一直在担心姐姐会在我生日寄送祝福,这下墨菲定律了(x)
虽然往常的作息能在睡前看到邮件,但是干饭困倦导致早上醒来开幕雷击
看了一眼答案还是觉得有点可惜,似乎错误来源在于特征值和正负号搞错,anyway,还好不算太寄(数电****)
简单回顾一下这门课:首先提醒,之后想来水学分的同学快跑,至少隔壁mmp比这个轻松114514倍(不知道明年会不会都本研贯通了,明年开通,今年还不算学分,**jwc),感觉大三上大部分时间都用在这上面了,yysy还是挺费事的
为什么这么费时可能有三个原因,首先一个是课程容量确实是大,想全部学明白确实需要花费很长时间消化。东云的终极速成以及b站上一些零散的群表可能有些帮助,但是我感觉东云似乎和姐姐有一样的问题,这里按下不表。本学期总共有7+1章,分别是群论基础、线性表示理论、转动群、点群基础、置换群的表示、李群基础、李代数+洛伦兹群简介。其中洛伦兹群没时间讲,点群基础由于太简单不好出考试题,所以本学期考试范围内的只有六章,其中主要时间用在了第二三章上。相比往年姐姐在群表上的功夫花的更足一点,后面又加了投影表示诱导表示,以及一些hear测度的东西;第三章则是和qm结合了一下,不过SU(2)和SO(3)可能就是我们最先接触群论的地方,感觉作为补充还不错。这里面最费时间的地方一个是在理解不可约表示的几个证明和定理上,第二个在于算群的不可约表示。不管是用算符完备集还是投影算子,都会被D4群来一点小小的计算震撼(我还以为是我的问题,突然发现之前也被Q到看来大家都是饱受折磨)事实上我还是最喜欢诱导表示,感觉是最自然的算表示方法,事实上我算群表第一次知道我在干嘛就是从诱导表示开始的,比照第一章看商群作为群的负载空间真的非常合理()。第三章的时候理解一下在函数空间的表示后面就会比较轻松(建议手动跳过姐姐的一些证明,特别是C-G系数)之后讲的内容大概都是为了给大家考试送分(bushi),虽然我没接好。讲真李群李代数可以多讲讲,感觉还是太蜻蜓点水了,可以看看GTM222,看起来还不戳。大致课程内容就是这样
第二个原因是我理解能力比较慢hhh,再加上秋季学期的晚上经常吃汤汤水水的东西,即使在第一排也会睡着(还是非常抱歉但真的忍不住),然后就需要花点时间再翻看,嗯,这是个很现实的原因
第三个原因在于感觉叙述重点的问题,姐姐似乎在不少地方十分执着于一些证明(虽然也不很数学),我的感受就是主体脉络不是很清楚,比如线性表示中,感觉突然就开始闷头证明几个不可约定理,(当时也是困),很多东西用的并不是很清楚,换一些别的证明可能又歇菜了,约等于还是啥也不会。事实上,我觉得这样其实可以稍微调整一下,把重点放在对于推导结果的理解上,对于式子本身意义的理解,怎么用,和前后的关系是什么,比如不可约正交定理说明了群函数空间基的数目和不可约表示矩阵元数目相等且一一对应,这还是一件挺神奇的事情;详细的证明可以只提一下用到了之前的什么东西,可以统统丢附录里。这样节省下来的时间可以讲更多的例子(事实上群表我还是不太会算),以及充实到李群李代数里去,感觉会更好。还有一个地方是有些碎碎念,东云给我的感觉也有一些,一些细枝末节有点多(可能和上一个有点重合),这个也不仅限于证明,包括一些概念的引入。关于讲义可能老师是为了让更多的同学来听课,不知道是不是我的问题看起来不是很好懂,疫情期间老师用的ppt感觉还挺好,所以非常希望老师线上讲(又有回放又有ppt,赢!)最后是感觉顺序上可以再调整一下,李群李代数的基础部分可以在第二章讲完有限群就加进一些,然后再讲转动群可能会好点。之前一直挺好奇升降算符的引入,也算是得到了一些小小的解释hh。可惜洛伦兹群没时间讲,还是有亿点点想听(不过自学不用考试也挺好)可能上课期间有无数种想建议的调整方案但新学期可能忘得差不多了,sigh,如果大家有什么想补充的可以在下面再来点,想发邮件说说想法
总之还是希望课程能越来越好,正如上面提到的似乎明年开始就改成本研贯通了,作为本科生旁听其实挺好而且不用考试也不用做一些剥蒜作业,不过对于想选课的同学还是挺好的,至少可以少凑4个学分()成绩图好像已经有xd附过了,姐姐还是hin能捞的www,拜谢一下奶爸()
- 课程难度:困难
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:中等
- 给分:超好
- 收获:很多
与量子力学同时修,果然极度舒适;加之是旁听,来去自由,每次来上课,都像在秘密花园艰难而饶有趣味地踱步。高雅的享受!
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:很多
大四老狗只想混个四学分顺便学点东西,没想到今年选课的人巨多,而且占座现象严重,所以果断翘掉所有课程开始自学。作业量还好,总共收四次作业,每次一两个晚上就能写完(不追求全对的前提下
最后给分出奇的好,空了一道15分的大题总评依然有4.0
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:很多
先说,zjjyyds,物院zjj潘爷刘国柱就是我心中的天花板。
21秋完整学完了这门课,本科时候选过这门课,由于当时整了三四十个学分,后面太浪两周没有听课,然后就跟不上了,因为讲义不听课看不太懂也没有找到合适参考书(其实是韩其智书),无奈退课。这次一节不落下的全部听完了,完成了自从16年进入科大以来“至少有一门课完全没有翘过课”的愿望,当然收货也是巨大的。
内容非常实在,课程顺序是群论基础、表示、转动群、点群、置换群、洛伦兹群、李群李代。对于第一次学的同学可能觉得像填鸭,原因是这些内容塞到一个学期确实有点多了,而且朱老师也想帮大家打下一个好基础所以很多地方都想讲一下。从转动群的后面就开始起飞了,洛伦兹群更是用拖堂的四五十分钟干完了,李群李代直接开启了ppt模式2333
课下是需要花一些时间吸收的,实在不懂可以参考韩书,初学者马书还是不要看了,纯纯折磨人。朱老师对于学生问问题也很负责,每次下课都会解答很久。
对于本科大三大四的同学我建议这个课和杨焕雄现代数理方法(可以参考我在那个课的评论)还有高量配合食用效果较佳,杨老师会对后面起飞的李群李代做很多补充,而且从转动群开始就可以起到相互参考的关系。
本来打算难度评成困难的,但是想了想确实远没有大一啃力学电磁学吃力,我还是大三之后过得太安逸了,对于大部分我们学校本科生和外校研究生而言确实属于中等难度,主要花时间一定可以学到不少东西。不想花时间应付考试也完全没啥问题,题目简单而且朱老师又是远近闻名的大善人……
- 课程难度:困难
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:很少
- 给分:超好
- 收获:很多
谢谢,被朱姐姐暖到了
在第二三章一脸懵逼的情况下,六七章基本不会的情况下硬是被朱姐姐奶到了优秀
我为我之前考完试而怀疑朱姐姐突然黑化而感到十分惭愧,同时也为没有好好学群论而感到十分惭愧
课程内容基本上前人述备矣,这里讲讲我上这门课的感受:
1、这门课虽然给分很好,但是如果想学好这门课一定要在课后认真复习、理解并做一些计算(比如自己手动算一些群表示),不然很容易被课程难度给整自闭以至于跟不上朱老师的节奏;
2、这门课容量非常非常大,比朱姐姐的理力内容不知道要大到哪里去了,所以被朱姐姐理力给暖到的同学,一定要先估计一下自己的课余时间是否充裕,并不建议在时间不充裕的情况下选这门课(比如同时还要学dzj的计算物理A的同学选这门课很有可能会放弃治疗)。虽然群论给分更温暖人心,但是在学这门课的时候心态容易爆炸;
3、群论搭配量子力学一起食用味道更佳。尤其是第二章末尾朱老师会讲射影表示以及第三章SO(3)与SU(2)在角动量理论中的应用,对帮助理解QM有极大作用。
然后关于final,可能是朱姐姐认为我们寒假四十多天会认真复习,所以整了张巨难的卷子我是不会告诉你一眼望去我只有杨图杨表杨算符的题会做。考试两小时迫真是现学现考,考完出来双眼无神还以为是我没有认真学群论所以被朱姐姐打击报复了没想到大家都差不多的感觉但这也有一点好那就是没有什么值得害怕了大不了放弃成绩。总之认真复习是王道,不要老是想着朱姐姐卷子简单就能混分因为你并不知道朱姐姐会不会来,骗,来,偷袭二十多岁的带学生,功夫还是要下在平时的。
- 课程难度:困难
- 作业多少:很少
- 给分好坏:超好
- 收获大小:一般
- 难度:困难
- 作业:很少
- 给分:超好
- 收获:一般
楼上都给了朱姐姐很高的评价 看来都是认真学了
我从一个划水者的角度冒昧评价一下这课
因为我去的晚 每回都抢不到前排 上课根本看不见老师板书 最后直接不去上课了
算是认真地看了一下老师的讲义 感觉和上课讲的差别挺大的 所以还是建议去上课抢前排听一下
老师最后会给参考题 说实话挺有用的
考前突击了可能有三四天吧?最后89调到95 当然突击的时候有隔壁的julao帮助(他卷面100)
因为是开卷 所以可以提前去图书馆借一些书 随便看看上边的题
2019秋成绩
| 人数 | 平均 | 中位数 | 优秀人数 | 优秀率 | 不及格数 | 熵 | 基尼系数 |
卷面 | 171 | 69.5 | 72 | 25 | 0.15 | 40 | 2.540 | 0.0602 |
总评 | 186 | 78.1 | 83 | 89 | 0.48 | 13 | 2.161 | 0.0539 |
- 课程难度:困难
- 作业多少:中等
- 给分好坏:超好
- 收获大小:一般
- 难度:困难
- 作业:中等
- 给分:超好
- 收获:一般
体验极差,可以说是上大学以来专业课除了数电体验最差的一门课
在课时明显不够的情况下,安排这么多内容十分不合理。每堂课都使劲抛出新的概念,在上一个概念还没有理解清楚的时候下一个概念又来了,搞得我非常痛苦
最逆天的是国庆之后要提前二十分钟上课,然后最后还要再拖堂二十分钟???
沟槽的为什么就不能多安排一点课时,或者分成两个学期来讲???不是讲的越多学生就能懂得越多啊
感觉如果课时能给多一点,体验应该能大幅度提升,毕竟老师的讲课能力感觉还是很可以的
绷不住了,总评给了4.3,老师是真的能奶
应该是考的实在是非常非常浅显的原因,甚至有的讲义上直接就有答案
太奇怪了太奇怪了太奇怪了!!我只能认为绝大多数同学和我一样都没有学懂这门课
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:很多
老师和助教都认真负责。 课时不够真的很遗憾。朱老师的意思是,给物院学生的高级数学课很少,所以他能讲多少讲多少。我对此并不完全赞同,我觉得有多少课时就干多少事,来选这门课的大部分同学积极性,都足以在课下补全必要的细节,或者直接略过。这门课花大量的时间讲证明细节和举例的计算,建议明年压缩这一部分。 至于内容的广度,我给好评,李群李代数开个头,也算是在拓展了。so3真是一生之敌,讲了好久还是没懂,尤其后面卡西米尔算子。想来,这门课我最大的收获,还是特征标理论吧。
- 课程难度:中等
- 作业多少:很多
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很多
- 给分:超好
- 收获:很多
这门课诚如上边的大佬所说的,不适合想要深入学习数学的人来学。但我还是愿意给朱姐姐9分,一来是因为朱姐姐讲课用心、待人热诚,二来是因为这门课对于学物理的人确实很有启发。量力里面的很多结论的源头就是群论,学了这学期的知识之后,至少我能看懂SO(3), SU(2),能自己手推角动量理论了。我认为这些知识对于想要进一步学习物理的人是非常有益的。当然,最值得称道的一点还是朱姐姐十分能奶,值得信任!
- 课程难度:中等
- 作业多少:很多
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很多
- 给分:超好
- 收获:很多
先占个楼。本人大三,选这门课的同时在学量子力学A。
这门课的大纲是这样的:
- 群的基本概念
- 群的线性表示理论
- 转动群
- 点群(简介)
- 置换群
- 一般的李群、李代数
可见这门课的内容还是挺丰富的。与量子力学A的适配性不错。作业有点多,不过对于理解基本概念还是有帮助的,建议好好做。
由于一学期的时间有限,80个学时,要塞这么多东西确实不容易,可见朱老师讲这门课是尽力了。这门课的课时安排有些不合理。基本概念讲了一个月,线性表示理论讲了一个月,转动群讲了一个月。好了,置换群,一般李群李代数,没时间了。开始念ppt了,走马观花式的过一遍,完了(扣除的1分原因在此)。(助教甚至打趣称,这门课要讲160个学时才算够)(感觉这门课跟我上的那门量子力学A一样的,最后开始赶课)
期末考试前有样卷,复习时可供参考。
期末考完了,感觉这个期末考试的题比样卷难多了,题量比较大,我没做完。感觉要寄了。我首先承认一点,角动量升降算符、角动量耦合、Wigner-Eckart定理什么的我是在这边学会的(smj的量子力学A今年这进度太慢了),这边讲转动群讲的东西很多。结果期末考试只考了个6分简单题?偷袭是吧!
以下内容编辑于出成绩以后:
朱老师在正式出分前是会以邮件形式把你的总评发过来的。这一点很好。我没想到,我这水平都能被捞到95分(4.3)?给分这么好!谢谢老师助教捞捞!
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:很多
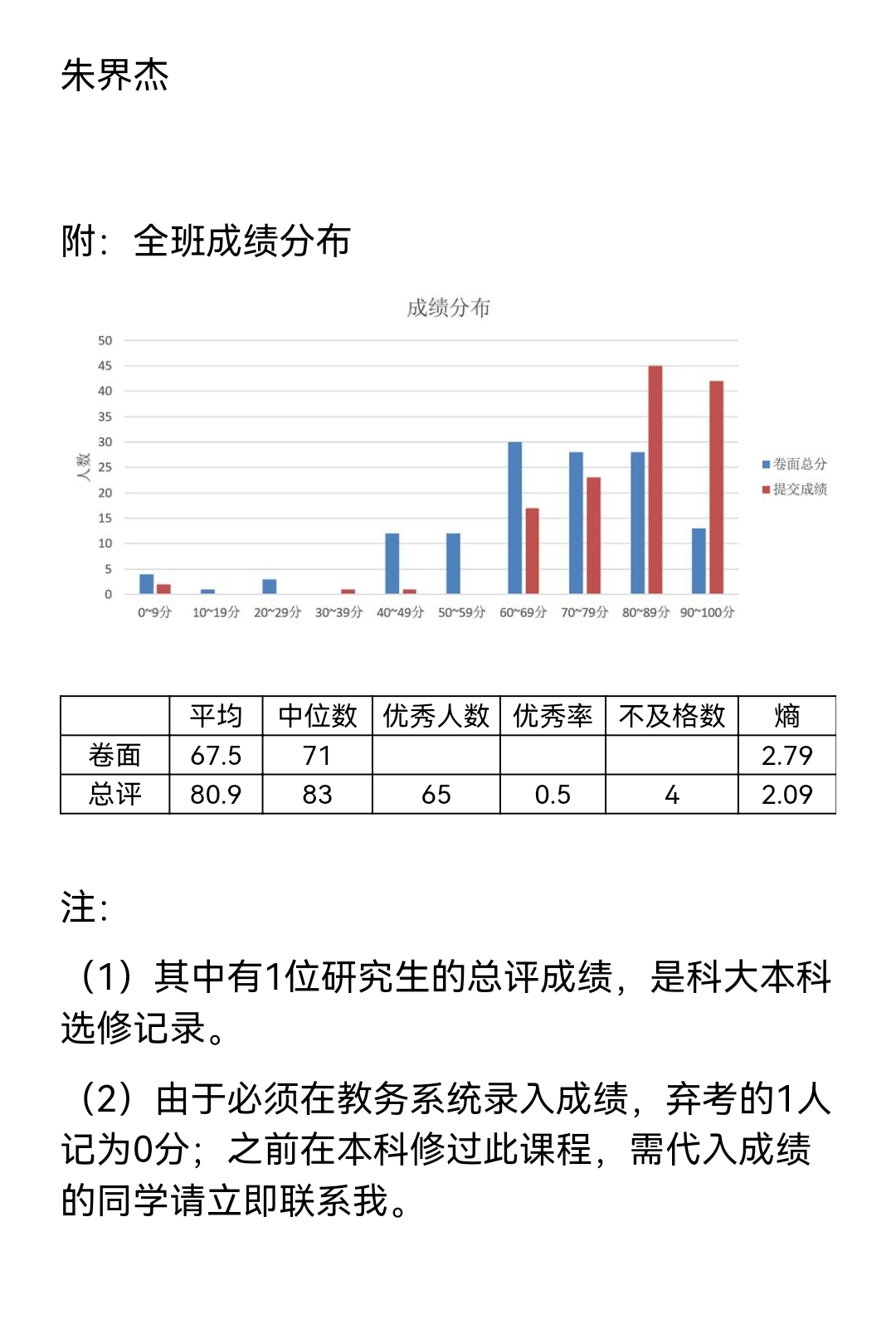
这门课内容确实多,很多内容都是偏数学的,上到后面速度越来越快(加一份血书求开两学期想把李代数再多学点),不过朱姐姐讲课一直都力求把概念讲得细致明白,所以只要上课认真听课下认真写作业考试完全没有问题。
朱姐姐凌晨发邮件出分,还贴了今年的成绩分布,不得不说真是神仙给分啊!
- 课程难度:困难
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:很少
- 给分:超好
- 收获:很多
写在前面的话:我非常推荐你上这一门群论课,首先我想告诉你这是一门面向量子力学和量子场论的群论课程(另一门群论及其应用PHYS7604P.01是面向凝聚态物理晶体、分子等体系应用的)。然而,即使你的侧重点是群论在晶体结构中应用,这一门课程也可以给你带来很大的帮助,你将会学到群的基本性质、群表示论、转动群、晶体点群、置换群以及李群和李代数,老师会将侧重点放在更基础的群基本性质和群表示论,包括你在高等量子力学中经常会提到的转动群,这对群论初学者的帮助非常大,有了这些基础知识,你在自己进一步学习群论的时候就会更加有方向性。
-------------------------------------------------先占坑----未完待续---------------------------------------------------------------------
2020年秋季考试成绩一览(摘自朱老师邮件)
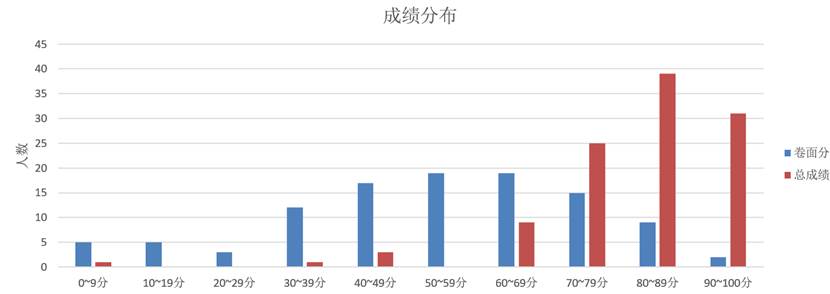
| 人数 | 平均 | 中位数 | 优秀人数 | 优秀率 | 不及格数 | 熵 |
卷面 | 107 | 53.5 | 54 |
|
|
| 3.023 |
总评 | 110 | 80.7 | 83 | 54 | 0.49 | 5 | 2.206 |
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:很多
给分简直不要太好,老师人也不错,课后答疑很耐心,总之选就完事了,吹爆!!
- 课程难度:困难
- 作业多少:中等
- 给分好坏:超好
- 收获大小:一般
- 难度:困难
- 作业:中等
- 给分:超好
- 收获:一般
我就说一点,朱老师考前会给出“样卷”,大概是想让我们看看考试怎么考,心里有点数。 但是我这里奉劝学弟学妹不要相信“样卷”的难度就是考试的难度。
因为考场拿到卷子我才发现,“样卷”并没有让我心里有数,相反,是让我心里没了点*数,竟然naive地考前不停毒奶,以为考试会非常轻松,我大意了啊没闪!结果是,拿到卷子一眼看去会做的就只有置换群的送分题,嗯,15分,其他85分咋办(・o・)?
“样卷”里出了迷向张量的题,是我唯一没在意的题,因为其他都会,这题不要了也罢。考试确实也考了迷向张量,嗯,我认了这分我不要。但是,“样卷”里其他会做的题都换了或者升升升级了...正应了《多情剑客无情剑》里那句“到头来却什么也没得到”,嗯考前觉得会很水于是一直在看小说,我错了(><)
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:很多
信息量超大的一门课。
几门可以拿出来单独开的课合在了一起,变相地说明了这门课有多么的浅显,实际考试有多么简单。期末脑子抽最后一道大题没写,考80分拿了92的总评,这生猛的调分,这友好的难度,这科普般的知识量,还不赶快选?????
ps:作业还是要做一下的,否则绝对会爆炸。
- 课程难度:困难
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:很少
- 给分:超好
- 收获:很多
这门课实际上仔细讲了群论基础(就是数学上的一些定义和定理),离散群的不等价不可约表示,量子力学里要用到的转动群;后面的点群一带而过,只讲了一些基础思路,置换群内容讲的简略但是考试是肯定会出题目的(并不要求证明,就是用课上讲的规则画画杨图,写写杨表,再填填特征标表),李群和李代数讲的真的十分简略,基本上只给了定义和定理的结论,没有给出证明(一来朱姐姐认为物理学院的同学们不太关心证明,二来教务处给的课时太少了啊啊啊)。
比较困难的内容集中在第二章,第三章(我是大二学选的这门课,没有量子力学基础,刚开始学时对第三章的逻辑没有把握好),需要课下多下下功夫弄明白;第五章的作业题一定要能全部做对,这是考试时的送分题,朱姐姐不会上传这一部分题目的答案,第六章和第七章里邓金图和嘉当矩阵要掌握好,实际上韩其智的书上给出了所有的单李代数的邓金图和嘉当矩阵。考试时其它的部分就要求我们要掌握上课讲的内容了,考的不难,弄清楚上课讲的例子就足够了,复习时要覆盖全面,不要认为课上没重点讲就不会考。
给分自然是超棒了,卷面82——>总评93。
大二的同学不要担心没有量子力学基础会听不懂这门课,其实是不需要提前学过的,只需要在讲到C-G系数前了解到量子力学的角动量理论就可以了。
- 课程难度:困难
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:很少
- 给分:超好
- 收获:很多
个人感觉课程难度还挺大的, 东西太多, 如果能开成两学期的课就好了.
虽然内容比较难, 但是朱老师很仁慈, 考试很水, 不用太担心.
- 课程难度:困难
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:中等
- 给分:超好
- 收获:很多
总的来说,这门课听过来体验较差,主要问题在课程安排上,一学期4个学分的课塞了6个学分的内容。老师提前40分钟开始上课最后讲李群和李代数也很赶,最后两节课讲完的。
内容安排,老师分了四章来讲,第一章是群论基础,第二章是群的线性表示,第三章讲SO(3)群,第四章是李群李代数初步。由于是物理系的群论课,老师讲的时候基本上不太关注证明,很多定理证明都跳过了,反而讲了很多物理上的东西,比如晶体点群和量子态的射影表示。学完之后的感受就是记住了很多定理和定义,而对这些东西的理解很浅。主要参考资料就是老师编的讲义
关于期末考试,最后出的题其实也就是用定理算一些例子,并不要求你对这些定理的来源和证明。期末考试跟讲义上的例题和作业题高度重合。难度主要就是看你考试的时候能不能想起来有这么个定理可以用来算这道题(我反正是因为考试的时候没想到特征标各行各列正交有道题没写出来)比较好的是老师会给期末样卷,知识点基本上能有50分的重叠。
关于给分,z姐姐的课有口皆碑,只要期末考试到了就能及格,优秀率也会尽量给满
- 课程难度:简单
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:简单
- 作业:很少
- 给分:超好
- 收获:很多
第几一节课有些事没来,第二节课来了发现课程群人满了加不上了……
- 课程难度:困难
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:中等
- 给分:超好
- 收获:很多
这是物理学院的群论课,内容主要包括群论基础、群表示论、李群李代数,以及群论在物理中的应用。数院同学可以看到很多群的实际应用,例如点群、典型群这些有几何意义的例子,以及它们在运动学、量子力学中的意义。数院专业课一般侧重于群的抽象理论,而这门课提供的实例就是很好的补充。
推荐数院的同学来旁听这门课,不过如果你没学好原子物理千万不要选课,否则会像我一样死的很惨(期末会考量子力学,老师当然不会给数院同学调分)。
- 课程难度:困难
- 作业多少:很少
- 给分好坏:一般
- 收获大小:一般
- 难度:困难
- 作业:很少
- 给分:一般
- 收获:一般
建议以后控制一下选课人数,每次都没有座位的体验实在是太差了()
- 课程难度:困难
- 作业多少:很多
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:很多
- 给分:超好
- 收获:很多
朱姐姐讲的非常好
考得很难,计算量很大,但是给分很好,希望这课课时能增加,多讲点应用部分的内容
- 课程难度:困难
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:很少
- 给分:超好
- 收获:很多
这门课内容非常多,主要篇幅在有限群的线性表示和转动群的表示,而李群李代数部分就讲得比较仓促。最后考试挺基础的,给分是没话说的。如果愿意在这门课上稍微多下点功夫,会相对比较容易拿4.3。
- 课程难度:困难
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:很少
- 给分:超好
- 收获:很多
又是一门话都被楼上说完的课……我就路过给个10分_(:з」∠)_
顺便扔个成绩分布各位感受下调分之猛烈_(:з」∠)_ (以下内容来自朱界杰老师的成绩通知邮件)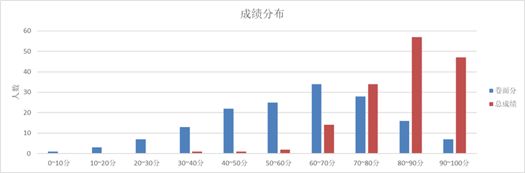
| 人数 | 平均 | 中位数 | 优秀人数 | 优秀率 | 不及格数 | 熵 | 基尼系数 | |
|---|---|---|---|---|---|---|---|---|
| 卷面 | 156 | 59.9 | 61 | 13 | 0.083 | 71 | 2.943 | 0.0899 |
| 总评 | 160 | 82.0 | 83 | 78 | 0.49 | 3 | 2.056 | 0.0358 |
注:有4位研究生的总评成绩,是科大本科期间的成绩记录。
- 课程难度:困难
- 作业多少:很多
- 给分好坏:超好
- 收获大小:一般
- 难度:困难
- 作业:很多
- 给分:超好
- 收获:一般
唯一见老师是在考场上,所以讲课质量不评价。
每周抄作业要抄半天,手残党慎选。不过不写作业也能参与考试并取得成绩,只是成绩会低一点。
考试开卷,及格很容易,基本不挂人。
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:一般
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:一般
事情少,给分 极好 的一门课。虽然这门课老生常谈的内容量和进度问题仍然没有彻底解决,但总体上瑕不掩瑜,我还是愿意给9分。
课程无点名无小测,有BB直播和回放。作业线上提交,课程没有助教因此作业无批改(估计是前面几年助教工作量太大了zjj不想找了),只要交了就满分。本来说不允许补交,但实际上可能是zjj忘记设置了,超时也能提交,所以最后决定考试前提交的都算数(
内容和进度上还是跟以前一样,前半部分是有限群和群表示论的内容,这部分内容讲的十分拖沓,老师会举大量的例子来说明一些概念。后半部分就是李群李代数的内容。今年不知道是不是zjj吸取了之前的经验,最后的进度没有那么赶了,并且也承诺最后一章不考(但是实际上还是考了,不过翻讲义套公式就行)。但留给这部分的时间仍然非常紧张,导致我什么也没学会,最后期末周只能花两个星期恶补。不过这个课配合高量角动量部分一起复习倒是意外地舒服,重合度很高,也算是变相给我节省复习时间了。
考试风格与老师的样卷极度相似,尤其第一题经典2026阶群,当时还想了半天1013是不是质数,zjj不会给人挖坑吧,所以从把小于\sqrt(1013)的指数全部验证了一遍。所以以后最好在质数年选课(bushi)。另外今年老师终于放下他心心念念的迷向张量了()
给分还是一如既往的奶,改卷本来就放海了,调分力度也是大的离谱(妙手回春啊朱大夫),无人挂科,优秀率远超40,也终于让我在最后一年的最后一门课拿了第一个满总评(哭)。毫不夸张的说,这是我在科大上过的给分最好的课了。
个人主观总结:想水学分推荐,想刷绩点推荐。不过要想听的舒服,最好有量子力学基础,要想有比较大的收获,还是要结合其他的参考书,课后多花点功夫,或者也可以和浣熊的《数学物理方法》搭配食用?
- 课程难度:困难
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:中等
- 给分:超好
- 收获:很多
物院大二,与杨焕雄老师《现代数学物理方法》一同选购。先说结论,内容庞杂,难度高,泛用性强,但一个学期内容塞爆也没讲完,中杯!(x)
和隔壁杨老师的课相比,更多着重于SO3与SU2,还讲了点群,但最后几节课一笔带过拓扑、根矢量等内容(两学期的内容量硬压到一个学期,下半学期每节课提前上二十分钟再拖堂十五分钟,最后勉强讲完)。课前会在bb系统发ppt和讲义,ppt相当于讲义节选再补一些内容(比如迷向张量)。一周两次作业,对着ppt研究一个小时就能做完。
本学期约200人选课,没有助教,共26次要交的作业,bb交了就拿满。期末前给出了考试范围(除了最后一笔带过的Dynkin图等之外基本都考),开卷2小时未加时,基本是作业难度。推荐打印讲义,并熟悉ppt里多出的部分。第一题用到了Sylow第三定理(翻了十分钟讲义才找到)。期末卷面91分(差不多前十名),总评97。调分力度很大!
总体来说课程压力是比较大的,有很多内容要学过之后沉淀一段时间再看一遍才能明白。讲义读得比较头疼(相比之下,杨老师的讲义虽然纯英但很通畅)。推荐喜欢数学的同学选购。
- 课程难度:困难
- 作业多少:很多
- 给分好坏:一般
- 收获大小:很多
- 难度:困难
- 作业:很多
- 给分:一般
- 收获:很多
我的评价是夯。
上课时间太阴间了,外加不点名,所以自适应将此课程调整为网课。
bb平台和瀚海都有录播,用猫抓可以下载下来,1.5倍速刚刚好。
学完还是有很多收获的。
- 课程难度:困难
- 作业多少:很多
- 给分好坏:超好
- 收获大小:一般
- 难度:困难
- 作业:很多
- 给分:超好
- 收获:一般
这门课我觉得很难,因为我没学过量子力学,但是这门课是需要你学过的。选这门课的原因是因为好奇,想知道啥叫群论,虽然我是等离子体的也用不到这东西,第一章其实还好,第二章线性表示理论我就完全听不懂了,感觉讲了很多概念,但我不懂他们之间的联系是什么,老师课上讲了几个例子,然后作业留了D4群的不等价不可约表示,不过我弄了好久也做不出来,后面的只是在课上听了个大概,但是课下仍然一头雾水,只能反复看回放,但是我也看不懂。不过我觉得老师讲的不错,毕竟我基础较差也能听个大概。然后老师的讲义很工整,看得出来老师是真的想让我们学会一些东西,课下也问过老师问题,老师特别耐心,即便我问一些可能很蠢(因为我根本没听懂)的问题,并且每堂课课后老师都会在讲台上站一会等着学生来问,这种老师我之前从未见过,太负责了。然后作业布置的很用心,前期的作业比较简单我还可以做一做,后期的作业我就看不懂了,毕竟我当时连指标运算都不熟。不过最后还好,我记得我的分数是74分,我已经很满足了。总的来说,如果你想选这门课,你一定要学过量子力学(因为后面多次用到了里面的概念,并且用到了很多运算比如那个‘<| |>’应该就是量子力学里的),然后最好之前就学过一点点群论,给分不用担心,我都这样了,估计卷面分也就20-30也都过了。