2025秋 2024秋 2023秋 2022秋 2021秋 2020秋 2019秋 2018秋 2017秋 2016秋 课程号:MATH100502
- 课程难度:中等
- 作业多少:很少
- 给分好坏:一般
- 收获大小:一般
| 选课类别:计划内与自由选修 | 教学类型:理论课 |
| 课程类别:本科计划内课程 | 开课单位:数学科学学院 |
| 课程层次:通修 | 学分:4.0 |
教学风格与课程内容
王新茂老师的《线性代数(A2)》课程以线性空间理论为核心,内容较为抽象,重点在于区分和理解矩阵与线性空间的关系。点评中反映,王老师往往将矩阵与空间理论割裂开教学,部分同学认为此方法缺乏科学性,因为它可能导致学生难以全面理解矩阵在空间中的作用。然而,王老师也致力于丰富学生对无限维线性空间的理解,这在他编写的讲义中有所体现,虽然这些内容在期末考试中并没有被考察。
讲义与作业
讲义精简而富有难度,适合有一定基础的学生深入研究,也有人认为不适合初学者。作业要求较为灵活,通常并不占成绩,然而完成作业的人普遍认为习题具有很高的练习价值,可以帮助深入理解线性空间背后的直观感觉。对于自学能力强的同学,王老师的课程被认为是自我提升的好机会。此外,有同学建议结合其他教材或资源(如李尚志的书或线性代数的网络资源)以更好地理解课程内容。
考核与给分
期中期末考试常与隔壁班统考,且偶数年与奇数年的出题安排可能不同。总体来说,考试内容相比课程学习中涵盖的内容基础,很多题目没有过多涉及复杂计算或高深理论。王老师给分较为宽松,调分幅度大,尤其是对于分数接近及格线的学生。尽管管理严格,他在出分后也会非常愿意处理学生的特殊情况,显示出对教学和评分的负责态度。
学生建议与反馈
许多同学称赞王新茂老师态度认真和友好,尽管教学内容安排不乏争议。推荐对线性代数有初步了解且自学能力强的学生选修,因为这门课在relaxation lesson安排上较为宽松。有同学强烈建议融会贯通矩阵与空间的联系,增加直观几何背景,以弥补教学中的缺失。对于希望挑战自我或需要课堂速通的同学来说,选择王新茂的课程可能会有特别的价值。
- 课程难度:困难
- 作业多少:很少
- 给分好坏:一般
- 收获大小:一般
- 难度:困难
- 作业:很少
- 给分:一般
- 收获:一般
“我只教基本的玩意儿”
“有的书上说‘空间为体,矩阵为用’,这是李尚志老师说的。李尚志老师是我的导师,我不同意这个理念。”
“网上有人说矩阵是奇技淫巧,这是统治阶级对劳动人民的污蔑!”
以此为嚆矢,我开始了上xxds的第四个学期。
期中考前,wxm 发表了一些餐前(大嘘)演讲:
我出题从来不卡人,卡人的题都是欧阳出的
我出题只卡那些不来听课的
期中不来就不来呗,那就期末赌一把,反正期末是欧阳出题
期中81,期末77,计算崩得有点严重,不知道能不能上4。重修只拿3.7太亏了。
出分90,这个 wxm 开课前承诺的“样条函数”力度还行。
线代(A2)的期中是各自考,而期末,大概是是偶数年王新茂出,奇数年隔壁出。这个规律最近几年都适用,所以最好提前做准备,不然考到不少 A1 的东西,要是忘了,哭都没处哭。
之后有时间再写点东西
两年wxm,一生打洞情
所以,究竟什么是线性代数?
首先,线性代数绝对不是打洞,至少不只是打洞。wxm 和 mj 都认为,线性空间比矩阵抽象得多,学起来更难。果真如此吗?大抵是
矩阵只需要打打洞、算算标准型就够了,理解线性空间要考虑的可就多了。
两年的线性代数学习下来,我深切体会到把矩阵论和线性空间“串联”而非“并联”是多么离谱的做法。当然,到了后期术业有专攻,数值计算打洞用的多、纯数线性空间用的多。但直接给人分到两学期,尤其是 wxm 的教材,那就是大一下强度拉满,大二上课时用不完。
另外,矩阵未必真比线性空间“具象”。说矩阵不抽象,大概的 idea 是不需要空间想象,只需要在一个数表上做计算就行了。但问题是,不了解背后的几何直观,而是嗯打洞,算到最后只知道算出了个比较好看的形式。至于为什么要这么打洞?“因为这样能打出来。”对于初学者,这种没有什么动机的运算实在是无聊。很多大一下同学,既对线性代数这一学科没有宏观概念,又不知道它有什么应用,只是机械地打洞,很容易削减学下去的动力。
我也是在大一下快期末的时候看了 3B1B 的《线性代数的本质》,才知道我为什么要学线性代数。但那时已经接近期末,再去从头再来已经来不及。于是 A1 寄了。至于 A2,我当时并不知道“奇变偶不变”的规律,选了叶先生班,但 wxm 出题,遂再寄,用 3.0 刷新了最低绩…
所以,初学者选 wxm 当然可以,但一定要对各种矩阵理论背后的空间背景有所了解,不然很容易打洞打懵了,压根不想学下去。
什么是矩阵?
矩阵就是线性变换。那什么又是线性变换呢?保持线性性的就是。
怎么样,听懂了吗?没听懂说明你直接听 wxm 的课也是会卡住的。
以 2 维空间(也就是平面直角坐标系)为例,我们允许对向量进行拉长、缩短(缩成 0 都行)、旋转,但不能掰弯!就像那种推拉门,推拉的过程中支撑杆夹角有变化,但彼此平行、相邻间距相等。
由于给定两个基向量,2 维空间的点可以被它们唯一线性表示。而线性变换就是能保持这个“存在唯一性”的变换。我们要求变换后也能“线性表示”,这直观意义就是对 2 维空间中的网格进行伸缩、旋转,但保持相邻直线平行、且间距相等。
要做到这一点,我们要做的就是对且只对基向量进行变换,把它们从一对基向量变成另一对向量。举个例子,在 i=(1,0), j=(0,1) 基向量下,某点的坐标是 v=(2,3),也就是 v=2i+3j。如果 i, j 线性变换成了 i', j',那么 v 就变换成了 v'=3i'+2j'。假设 i'=(0,1), j'=(0,-1),那么 v 在新坐标系下的坐标就变成了 v'=(-2,3)。
因此,我们用矩阵 A 去乘一个向量 v,那么相当于用这个矩阵对应的线性变换去“变基向量”,然后在新坐标系下 v 也有了新的坐标,这就是 Av 的意义。
既然矩阵是线性变换,那么矩阵乘矩阵自然就是线性变换的复合了。
还有一个重要的问题是矩阵能不能乘,与行数和列数有关。这是因为,m×n 矩阵左乘列向量,是将 n 维向量变成 m 维向量。m×n 矩阵是 n 维空间上的线性变换,只能作用在 n 维空间。
什么是矩阵的逆?
既然矩阵是线性变换,那么自然可以想到,矩阵的逆是逆变换,即“反函数”。当然,单位阵就是恒同变换(一动不动)。
那么什么样的矩阵可逆呢?别忘了,我们线性变换本质是基在变。如果我们把一组基还能打成一组基,那么这个线性变换才可逆。这也直接说明了可逆阵一定是方阵。如果不是方阵,例如 m×n,m>n 时是“升维”,凭空加了 m-n 个坐标轴,只要我们再把它去掉,那就无事发生,这就是说明它有左逆,也就是有个线性变换能让它“恢复原状”。但如果反过来,m<n,那么就是“降维打击”,你都给人家压扁了,怎么可能再恢复?因此它没有左逆。(右逆类似讨论)
而什么样的方阵才有逆呢?我们下面再讨论。
什么是行列式?
行列式的一种写法是 det A=|A|,那么我们会第一反应想到某种“模长”。
是也不是。
它不是范数,所以不是模长。但它确实带有某种“大小”的意味。这回以 3 维空间为例,考虑正方体 [0,1]^3。它由三个两两垂直单位向量张成,体积为 1。在线性变换下,它的平行的棱还是平行,所以我们会得到一个平行六面体。这个平行六面体的中的点,就是 A 作用在 [0,1]^3 中的点对应的向量得到的。
而 |A| 就是这个新的平行六面体的体积。比如 |A|=114514,那么新平行六面体的体积一定为 114514。更一般地,对于三维空间中的任意几何体,设它的体积为 V,那么在 A 的作用下,它的体积就是 V'=|A|V。对于二维,则将体积改为面积。如果学过叉乘、混合积,就会对行列式的“放缩”性质产生更深刻的理解。
好了,那么行列式为零是啥意思?显而易见,对于三维,那就是把任何一个一个空间几何体的体积都能打成 0。想要以“线性”的方式把体积变为 0,那就是通俗易懂的降维打击。比如把一个球压成圆,甚至压成线段、压成点,都能达到这样的效果。这种情况下,这个线性变换对应的矩阵的行列式就是 0。自然而然地,如果只是“揉揉搓搓”,那还是能变回来的,但降维打击了,铲都铲不起来。这就是为什么方阵可逆等价于行列式为 0。
另一方面,行列数不相等的矩阵,直接给升维或降维了,当然也没法定义“体积”的放缩倍数,也就没有行列式了。
什么是秩与相抵?
前面说到,一个线性变换可以把一个高维的东西打成低维的,那么究竟打成几维?秩是几维那就是几维。
这通过相抵能更容易看出来。对于一般的基,一个线性变换作用上去,可能把这组基打得乱七八糟的。我们希望找到一组好一点的基,当矩阵作用上去后,可以“不怎么动”。那么,我们要提前做准备,也就是把提前把基换一下,从一组基到另一组基的变换,需要乘一个过渡矩阵。基换了以后,我们可以接受线性变换的洗礼。但这还不够,还需要“物归原主”,也就是把基变回去。当然有时候降维了,基就没这么多了,那能变回去几个算几个,所以还要再乘一个过渡矩阵,它的大小可能就和最开始那个不大一样了。这实际上就达到了 A=Q^{-1} Σ P 的效果。由于基变完了还得是一组基,所以我们要求 P Q 可逆。
相抵的理论告诉我们,最中间那个 Σ 可以长得很好看,即 Σ=diag(I_r, O)。这时候,后 n-r 个向量就被线性变换 Σ 打没了,因此一个 n 维的东西被打成了 r 维的。P,Q 可逆,所以不影响维数。至此,我们就能看出秩 r 的几何意义。
什么是相似?
相抵中,P,Q 未必相同,所以可能走了一圈回不了家了。我们希望怎么过去就怎么回来,即 A=P^{-1} B P,这就是相似。
换句话说,我们研究相似的目的,就是看这个线性变换比较糟糕,希望在一个新坐标系下面会好一些。直观理解,就是送过去、做变换、原封不动拉回来。
但是,并非所有线性变换都能相似对角化,在任何一组基下,都做不到“只伸缩、不旋转”。不过,我们还是可以把它“分而围之”,将矩阵分成 Jordan 块,每一块内部长得难看一点,但总体还是个准对角阵。而准对焦阵每一块,就是一个子空间。子空间内部可能无法做到只伸缩,但可以构成一个循环,通过不断作用某一个向量,生成整个子空间的基,这就是循环子空间。也就是说,Jordan 标准型正是线性空间的循环子空间分解。这可能是我们能做到的最好的结果了。
什么是特征值?
wxm 会告诉你,特征值是特征多项式的根,但这和没说没啥区别。我们从 Av=λv 来看,这正是做到了只伸缩、不旋转。对于特征向量 v,A 作用上去就会把他变成同方向的 λ 倍(由于 λ 可负,所以可以反向)。
当然,不是所有矩阵都有这么好的性质。如果它可对角化,就意味着可以找出一组基,这些基向量全是特征向量。在这种意义下,我们在所有方向上都可以只伸缩、不旋转,这也是为什么可对角化的矩阵这么好。
不可对角化也没那么糟糕,我们可以将它相似三角化。以 4 维为例,线性变换后,x'轴方向我们可以只伸缩。但 y' 方向不行,非得带个旋转,那我们可以做到只带 x' 轴方向的旋转。而 z' 轴可能就要把前俩都带上了,但仍然可以不带 w' 轴…
另一个重要的结论是行列式等于特征值的乘积。很显然,每个维度变成原来的 λ_i 倍,那么整个的“n 维体积”就变成了它们的乘积倍。
什么是正交?
我们前面谈了这么久的只伸缩、不旋转,那能不能倒反天罡?
当然可以,如果一个方阵它能让基向量“只旋转、不伸缩”,而且这个旋转是刚体的,那么它就是正交阵。
因为是刚体旋转,所以正交阵保夹角,进而保垂直。所以它的等价判定是将标准正交基映到标准正交基。
另一方面,正交阵不伸缩,所以特征向量模场只能为 1(可能是复的)。
什么是正定?
矩阵可以左乘可以右乘,但小孩子才做选择,大学生我都要。
矩阵当然可以左拥右抱:左乘一个行向量,再右乘一个列向量。当它是方阵时,那么写出来就是一个 n 元二次多项式,所以我们只研究方阵。进一步,二次多项式的交叉项由矩阵里的 2 个元素决定,我们自然可以让它们一人一半,所以只要研究对称阵就行了。
陈计名言:所有代数不等式的本质是 x^2≥0。那么,推广到 n 元肯定也是我们想要的。因此我们想要一种对称阵,它左乘再右乘同一个向量后,永远是正的,除非它是零向量,那这就是我们要求的正定阵。
一个很直观的理解是,正定阵诱导的正定二次型,在每个方向都是“抛物线开口向上”,平着也不行,到了谷底就赶紧上去。而如果有个方向比较平,那么它也能保证非负性,但零点会不止一个,而是一条线、一片乃至更多,这就是半正定。负定和半负定也是这么来的。如果有正有负,也就是有的方向开口朝上、有的朝下,那么就是不定。
正定要求各主子式为正,或者特征值全正,也是出于这般考虑。但凡有个负的,那么就会出现“负体积”或“反向伸缩”,就不能保证恒正了。
至此,wxm 讲义上大多数重要概念都有了线性空间的直观性。
假如当初的我也能体会到这一点,也不至于在这上面驻足两年了罢…
看起来 wxm 还要统领线代 A 好多年,只能祝福后来人尽可能趋利避害,各取所需。至少,我不希望再看到两年王新茂的悲剧发生了。
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:没有
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:没有
除了给分很好以及老师上课很认真之外其他都很难称得上好的一门课,线性空间和矩阵完全脱节,基本上还是要靠自己找题去练,尽管考试都是一些简单无比So easy的计算题。一学期下来你会发现其实根本没讲什么东西,只是给你罗列了线性空间,线性映射,内积空间的基本概念和定理而已。 不是说老师教学不能创新,只是王老师的这种A1阉割掉线性空间A2只讲线性空间的做法绝对是不科学的。建议王老师去带线代B1,他的讲法对于线代B的同学应该是非常适合的。
- 课程难度:困难
- 作业多少:很少
- 给分好坏:一般
- 收获大小:一般
- 难度:困难
- 作业:很少
- 给分:一般
- 收获:一般
秋季学期占个坑先。 本学期第一节课wxm提出了劳动人民与统治阶级理论,矩阵象征劳动人民,空间象征统治阶级。且看本学期wxm带我们如何实现从劳动人民到统治阶级的跨越。
- 课程难度:简单
- 作业多少:很少
- 给分好坏:一般
- 收获大小:一般
- 难度:简单
- 作业:很少
- 给分:一般
- 收获:一般
有关xm的线代具体参见我在A1的评课(现在xm讲义习题解答已更新完成,稍后会上传个人主页),这学期稍显离谱的是,期末统考(并且不是选做的那种,是直接一起考),而两个班的顺序并不同,导致一道难题完全来自上学期的内容(隔壁班这学期的内容),坑害了不少人(
- 课程难度:中等
- 作业多少:很少
- 给分好坏:杀手
- 收获大小:没有
- 难度:中等
- 作业:很少
- 给分:杀手
- 收获:没有
一学期没上过课也没学过 考试只会做期中的1和期末的68这些初等的题 别的一概不会 被挂也算合情合理 不过调分力度真的不如A1 还以为交了作业能给我捞到及格呢💦 (先给个3分 补考过了+2 补考没过-2
(差点把这事忘了💦
补考擦线过了 从身边人反应看补考给分手还是比较松的 评分+2(
- 课程难度:困难
- 作业多少:很少
- 给分好坏:超好
- 收获大小:一般
- 难度:困难
- 作业:很少
- 给分:超好
- 收获:一般
王新茂你是我爹!!!
此生无悔入茂门!!!
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:很多
期末考完来写个点评。考试结果心里已经有个数了反正无比凄凉,难的做不出简单的犯唐算不对。
相比之下王老师的A2是比A1轻松不少的节奏也慢些,给这学期其他课留了不少时间。主要就是线性空间的介绍以及对A1中矩阵相关定理的解释。比较独特的在于无穷维空间的性质。按他上课说的,“有限维的都是初等代数”“空间与矩阵不同之处在于空间可以研究无穷维”。不过由于考试时统考,隔壁班好像不怎么讲无穷维,期末考试没有体现。由于有时间,老师还花了五节课左右时间讲了张量积内容(这好像是这学期才有的)。
对王老师个人的评价在A1中已经叙述。简单说就是感觉人其实是很和善的上课也还是不错的。
期中考试是8.1-9.4,内容不多基本上每小节考一次,比较好复习,考的也很好。期末考试内容是线代所有内容,其实说难也并不很难,没有太多很难想的,但是由于种种原因大型坠机。希望老师能捞捞🥺🥺🥺
更:光速出分。虽然犯唐凄凉,但可能由于整体糟糕,老师改卷感觉水放完了,总评不至于过低。
综合A1A2四次改卷来说王老师改卷没得说吧。没完全出来的能给已经尽量给了,写的疏漏的也肯定会扣,查了几次分看到详情也是心服口服没话说。
哭了,给茂爷跪了,居然给了A+。感觉期末分数不止开根乘十。此生无悔入茂门😭
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:一般
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:一般
由于上学期花巨大篇幅讲了极富技巧的矩阵代数(1-7章),这学期讲线性空间(8-10章+多重线性代数)显得有些空洞,明显可以感觉讲课速度变慢了不少。
有种用心学了A1的5个学分之后送你4个学分的美感,你怎么知道我这个学期每周只做一道作业题,想要划水还是来王老师班上吧
期中考试是王老师自己出题,只考空间相对容易
期末考试是统考,矩阵和空间一起考(感觉和隔壁班进度更贴合),因此A1知识是不能忘的(5道大题就没有纯考空间的,相当多技巧都来自A1内容)
感觉王老师的线性代数考试要用心学了不会太低,毕竟王老师有原话“技巧用多看都是套路”,不过要是不学的话会被杀得很惨(
今天出分了,由于考试太难王老师猛猛捞人,感觉幅度已经超过开根号*10(也许是按照排名给的),给分肯定算是“超好”了
不过无论如何考题确实是相当硬,运用的技巧也相当综合,想学好肯定是要付出相当多时间的
以下是同学的数据:
- 100 + 70 = 95
- 84 + 80 = 95
- 50多 + 80多 = 91
- 55 + 37 = GPA 3.3
贴一些考试数据,供来者参考。
似乎每次考出来都是双正态或者均匀分布(
期中考:
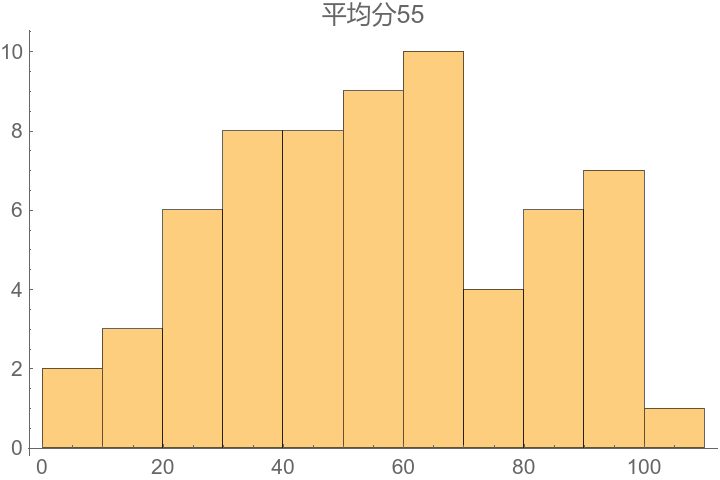
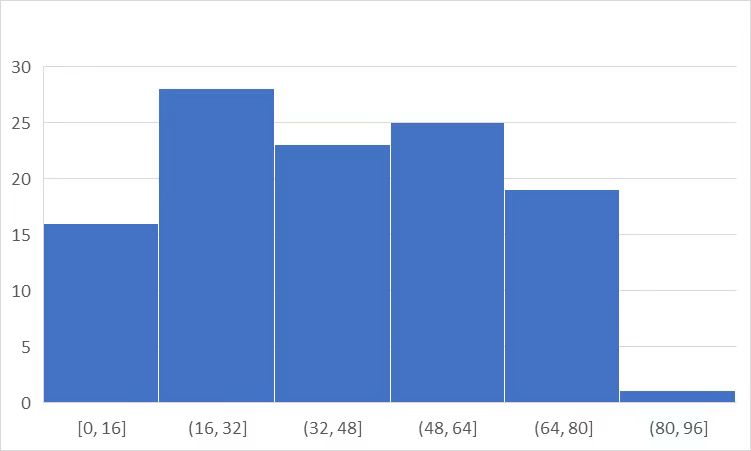
期末考我们班均分41分,没有公布成绩分布图。放个隔壁班的分数分布图(平均分42)
- 课程难度:中等
- 作业多少:中等
- 给分好坏:一般
- 收获大小:没有
- 难度:中等
- 作业:中等
- 给分:一般
- 收获:没有
王新茂
研究方向:计算数学
职称:副教授
selected publication: none.
publication in the recent five years: none.
考试是两个班统考。
同学们,看到这些信息,你想到了什么?
快跑!
- 课程难度:困难
- 作业多少:很少
- 给分好坏:杀手
- 收获大小:一般
- 难度:困难
- 作业:很少
- 给分:杀手
- 收获:一般
整体学完发现最后自己最熟悉的还是那些矩阵技巧,觉得自己没有领会到利用不变子空间,循环子空间推导Jordan标准型的精髓。不能苟同王老师以矩阵论为教学中心并打洞出Jordan标准型的教学思路。整体学下来和预期有比较大出入。
另外王老师的超精简讲义作为教材来说,真是太不合适了。不仅趣味不大,例题只有精妙步骤(缺少基本思考方向,不适合初学者),习题安排也不合理。更像是给人欣赏的,而不像是想教会和我一样的大多数普通学生。
给分方面听闻连续两次比平均分少10分就只有1.x绩点,似乎也有不少同学拿了科大最低绩。这也侧面反应了给分杀手吧。
- 课程难度:简单
- 作业多少:很少
- 给分好坏:一般
- 收获大小:没有
- 难度:简单
- 作业:很少
- 给分:一般
- 收获:没有
考完了期末来吐槽一下吧
这个A2相比于A1真的是水完了,几乎没有什么实质上的内容,即使是无穷维的情况也都只是当做一些神秘反例而已,而且个人感觉在无穷维空间只考虑线性代数里的东西意义确实不大,比较有意义的部分可能是在于拿空间语言来解释很多的矩阵定理,但如果习惯于A1的只用矩阵做出这些会感觉太“水”。总之学有余力的同学可以翘掉所有课,反正期末考也几乎只考A1内容(两个班顺序和重点完全不一样来统考真是幽默完了吧),拿到卷子真笑了,大题第一道求Jordan标准型的题目几乎和25春A1期末考一模一样吧,感觉这半年的线性代数是几乎没有学的,但只要记牢A1内容考试还是能考的。当然很炸妈的是这卷子考了一堆A1里矩阵奇异值分解QR分解之类的东西,在A2里面几乎没用过真会忘光。王老师自己也评价A2比较水,就是在“学说话”。
个人觉得对自己水平比较自信或者想划水的同学都可以选王班,一周交一次作业(可以发邮箱交电子版),平时每节课要按照学号填写签到表,大大提高了到课率。
出分了
听说今年给分是爸爸级别,那还是打个10分吧
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:一般
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:一般
前人说的已经很全了,但我还是想强调:如果你对自己的自学能力有信心,或者自学过线性代数,那么可以考虑来wxm班。这里没有小论文,作业只用交18道任意的线性代数题,期中期末只考察最基本的东西,调分也很猛(奶力只有隔壁wffc可以相提并论)。
最后,虽说A2比A1简单不少,但我在学习的过程中还是碰到了诸多困难,感谢两位助教哥哥总是热情地解答我的问题,谢谢你们(≧∇≦)/!
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:一般
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:一般
上了两个学期的wxm线性代数了(而且两个学期都是个性化到王班上的),总体感受是比较不错的。第一学期比较naive,认真阅读讲义或者听课,受到了一点小小的矩阵震撼,于是狂做wxm习题,不会的就硬花工夫想,那种打洞打半天的题也做了,属实是题瘾犯了,唉。第一学期后半段老是看隔壁班的人使用空间语言吹牛,于是看了一下LADR,感觉和wxm相比,这上面在讲一种很新的线性代数。第二学期感觉内容比较少,就直接开摆了,开学两三周之后就根本不去上课了,作业也不写,还是最后一周补交的整个学期的(这里必须要感谢一下助教)。
总体来讲,wxm讲课水平应该还算可以,内容选择这块很多人批评过,我也觉得不甚合理。我认为如果第一学期以矩阵论为核心内容,也应该适当引入空间语言,可以不严谨地讲,只是作为直观辅助,这也可以避免wxm老师对于空间和矩阵逻辑先后顺序问题的担忧。wxm讲义我认为也是写的不错,内容比较精炼,适合速通。应对wxm老师的考试,除了掌握基本内容,可能需要重点把时间花在课后习题上,原神的作业题答案很有用,比较难的题看看答案就行,自己做纯属浪费时间,以我这两学期的经历来看,可能看课后习题的难题根本就没啥用,出题比较基础。
最后回到线性代数这门课,在数院和少数培养方案中,这门课都是大一下才开课,是比较晚的,所以我相信有相当多同学在修读这门课之前已经了解了一部分内容了,而且对于这种基础课,花在上面的精力可能不需要太多。如果你愿意自学线性代数,那我还是相当推荐wxm老师的课堂的,毕竟不点名,几乎没作业,速通难度也不大()。而对于想学习比较有代数意味的线性代数的同学,不推荐这个课堂。我还记着这学期wxm讲同态基本定理的时候一开始把ker和im写反了,之后我就再也提不起听课的兴趣了。。。
另外看到wxm老师因为其他课程上的教学事故导致班级都快开不起来了,感觉也比较难绷,我个人认为只要助教靠谱问题应该不大。
第一学期给分不错,这学期现在还没出总评,期中期末都上90了,先给这个课往上拉一点分,希望老师也给我往上拉拉,给个4.3吧。
哦对了,再补充一点关于线性代数的东西,李文威老师近几个月在主页上更新一本真·线性代数讲义的草稿,大家可以读一下,我没仔细读,但是李文威老师的水平还是相当值得信赖的。
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:一般
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:一般
一大早起来发现出分了,期中90(均分60)/期末90(均分51),4.3应该稳。
据说这次统考比较神必,偏重本班出题,考完隔壁班的人破防,不过为什么本班平均分比隔壁班还低(
本课程自我感觉上课体验不佳,主要是老师板书字小,后排看不清,以及老师思维过于跳跃,因此我后半学期就没怎么听过课了,全靠自学。我建议选wxm的学弟学妹提前做好预习工作,要不然上课真的会听不懂。
期末考试中规中矩。t1考迹的基本性质,以及经典的矩阵相乘化为张量积形式(这个事情告诉我们复习还是得看看上学期wxm打洞方法,这个方法作为经典方法出现过,上学期期末也考过,熟悉的同学可以直接写出答案)。t2是简单计算题,不过要想到构造内积还是卡了我一会。t3方法很多,第二问稀里糊涂凑出来了,运气好。t4作业原题(一定要把课后题做一遍!!!)t5简单计算题,没什么好说的。
以下是本人一点自学建议:
- 还是强烈建议把课后题都做一遍,做不出来的可以放着想一段时间,实在做不出来再去看答案,考试题方法不会变,都来自书内。你也可以在课后题中发现一些应用广泛的小结论,复习的时候可以记下来。
- 一定要自己多思考!!!上学期的矩阵打洞可以很好地帮助本学期线性空间的理解,记得经常思考一下这个线性空间的定理对应到矩阵是什么样的情形,例如最简单的,直和意味着矩阵表示是什么样的?循环子空间对应的矩阵表示是什么?等等。不会做的题也可以思考一下对应到矩阵来获取一些思路。
- 学有余力的同学可以适当补充一些线性泛函知识,比如正交补,正交分解等等。不过期末考试大概率只考有限维空间,补充这些只是为了增加理解。
- 线性空间,线性映射是线性代数的精髓,建议越早熟悉这些抽象的语言越好,方便后续深入学习。
- 课程难度:中等
- 作业多少:很多
- 给分好坏:超好
- 收获大小:一般
- 难度:中等
- 作业:很多
- 给分:超好
- 收获:一般
把之前的too simple的评课重写了一下,,,感觉看前面的评课大多也是大一大二同学写的,现在又学了一年半,我的评价是:如果想学数学那都不建议选wxm的线代。事实上我觉得上wxm的迫真课程是典型的在学字,一上来巨大多矩阵打洞让初学的同学无法看清线代究竟是什么,到后面好不容易开始结合线性空间的语言了,也不注重几何直观,最后硬塞入的半点被泛函分析完全cover的无穷维线性空间的内容更是不知道为了什么。感觉大多数同学(包括当时的我)都是刷刷讲义上的难题感觉做出来挺有成就感,考试出的不难给分也好,整个一套混下来具有迫真很满意。但是这样越到后面越是有害,碰到遇到线代的地方都比较容易蒙古,而那些所谓的打洞机巧,因为不被(显著地)用到,也只不过是沦为神必科气壬的谈资,这种人真叫他做个讲义上的题114.514%做不出来。
不过话说回来,我觉得这门课与其巨大讲一些没法用上的迫真内容,不如讲讲多重线性代数(陈省身的《微分几何讲义》Chapter 2)。你科数院好像没有好好讲了张量的本科课,但是并不是每个人都会修微分流形和黎曼几何,,,
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:一般
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:一般
学完两学期的线性代数一起评价。就王新茂的教学来说,A1应该比A2难太多。我A1只有85,但是A2期中期末都还不错,总评95。 王老师人真的很好,有不会的直接问他就行,老师会直接教你,再简单的问题都会!吐槽一下:感觉A2的助教没有A1的助教认真负责。。还是挺推荐的,毕竟给分是真的好!(A1期中期末都是70+,A2期中期末都是90+)
- 课程难度:困难
- 作业多少:中等
- 给分好坏:超好
- 收获大小:一般
- 难度:困难
- 作业:中等
- 给分:超好
- 收获:一般
首先,新茂给分真是超好的!!!本来算完成绩都要挂科了,他应该是调高了二十分… 但是!!!学了一学期空间理论,最后和隔壁班统考真的是无力吐槽!!! 希望来年重修A2的时候是新茂出题…
- 课程难度:中等
- 作业多少:中等
- 给分好坏:一般
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:一般
- 收获:很多
王新茂老师讲课特别清楚,定理证明现场想,有时翻车也会根据讲义及时纠正。同学们的反馈也很积极,班上dalao应该很多,气氛很好。王老师上课爱请人上黑板做题,不过和平时分无关。有时点名喊人上来,有时则是随便喊在座的一位同学。 而王老师的讲义则更是言简意赅,又不缺关键步骤。当然没有完全进入状态的同学可能会觉得有些跳步。(顺带一提,二次型化为对角形的步骤似乎少了一步,不知道现在有没有补上)矩阵部分有许多拓展的知识,比较偏矩阵分析(Jordan标准型也是打洞证明的233) 矩阵部分习题也较困难,从第五章开始完成作业感到吃力也不用太担心。作业的话除非你不及格不然是不算分的 但是能力范围左右在提示下可以掌握的题还是尽量掌握,这学期期末考试最后一道证明题就是讲义前面一作业题(虽说是陈小伍老师出的卷)线性空间部分王老师介绍了无穷维线性空间的性质,不过期末考试不涉及。线性空间部分的习题难度也有所下降。(跑偏了 扯了好多A1课程的事( 总之收获很大,最后自己考的也不错,得到了应得的成绩。想有所收获、挑战自己的话选wxm的课来听课绝对是不错的选择。
- 课程难度:中等
- 作业多少:很多
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很多
- 给分:超好
- 收获:很多
来答。 王老师是将矩阵和线性空间理论分开来讲的,A1基本上矩阵技巧玩的很6了,毕竟打洞来开辟各种标准型...到了A2,由于有限维的问题基本都能用矩阵来做,因此A2就是先把定义讲一遍,然后就进入无限维...这就特别sao,很有趣的~不过我觉得最好最后再看看Linear algebra done right这样以线性空间理论讲起的。 然后习题依然是默认全做,上个学期花了好多时间~这个学期比较顺手,讲义的习题质量都很有价值,并且一直在更新、在升华,为什么这样说,我注意到A1部分的一些例题和定理添加了了更有启发性或者更自然的思路。 如果你想学好线性代数,王老师的课不会后悔。
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:一般
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:一般
唔,wxm的线代A2,都是在补空间的知识,但是我A1就学的差不多了orzzz
咱平常不经常去上课,都是看教材以及各种各样莫名其妙的东西自学,做各种各样的习题+往年例题。
wxm的教材会特别介绍无穷维线性空间与有限维的区别,感觉还挺有意思。
教材课后习题有原神写的答案,很棒,很赞。收获很大
补充一点,确实要对自己水平有信心才建议选,wxm感觉是比较看成绩的那一类,我A1,A2都没交过作业,全靠期中+期末。得分都是4+。
- 课程难度:中等
- 作业多少:很少
- 给分好坏:一般
- 收获大小:没有
- 难度:中等
- 作业:很少
- 给分:一般
- 收获:没有
刚出分来评个课,新茂的A2基本都是空间的东西,不过由于他按照自己的讲义来讲课导致讲了很多期末不会考的无穷维的知识,感觉也很难听懂而且用处也不大。期末隔壁班出题,真是大跌眼镜,这么多计算给非数的写写不行吗,我考前准备的上学期积累的很多矩阵难题有一次扑了个空,有点失望说实话,算一堆过渡矩阵我实在不能理解有什么意思,这学期除了考前半个月就没怎么碰过线性代数,不过想复习的话还是建议速通一遍新茂讲义的定义,练习的话就换个稍微正常的教材吧。利益相关期中87均分69好像,期末76均分49,总评90+应该问题不大,考虑到一学期都是混下来的,也算是不错了,此生脱离新茂了。
- 课程难度:困难
- 作业多少:很少
- 给分好坏:一般
- 收获大小:一般
- 难度:困难
- 作业:很少
- 给分:一般
- 收获:一般
A1被折磨到想死,A2总体比A1舒服点 第九章可能会有一点难 其他的部分难度适中吧 不过感觉A2没A1奶了(? A1 期中高均分16 期末低均分5分总评78 A2 期中高均分16 期末高均分20 总评88 不过我这种废物能3.7已经够赏脸了( 不过说实话 对于计算来说矩阵确实很重要 虽然新茂A1难但是啃下来收货还是蛮大的
- 课程难度:中等
- 作业多少:很少
- 给分好坏:一般
- 收获大小:一般
- 难度:中等
- 作业:很少
- 给分:一般
- 收获:一般
A1选了王新茂,A2只好继续选。对像我这种水平中不溜的,说不上推荐,也说不上不推荐。班里几个大神都很喜欢,但似乎调分不如隔壁叶郁给力。所以建议大佬来王班,讲义里不少大学生数学竞赛难度的题;对实力不太自信的可以去叶班,A1期末叶班平均分才28,但有些个位数的人都调到及格了。
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:一般
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:一般
这学期只讲空间,老师讲课讲得很精简,清楚。作业自由度也比较大。期中期末比例2:8。然而期末考试陈小伍老师出卷,个人感觉做起来极其不顺,也有可能是自己学得不太扎实。。。最终考得极其爆炸估计60-70左右,然而wxm老师调分大法非常棒,大约调高了20分。 但我感觉可能按照李尚志的那本书学可能会更好一点,虽说舍弃了无穷维的内容,但是对我这样的学弱应该是更好理解,并且能够得到一些常规题的练习不至于考试的时候不太会做题。
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:很多
王老师很认真负责,讲得也很清楚。只是与A1相比,A2感觉内容比较少,可能有一定的反差。
- 课程难度:简单
- 作业多少:很少
- 给分好坏:超好
- 收获大小:没有
- 难度:简单
- 作业:很少
- 给分:超好
- 收获:没有
在这里只要粗略学过主流路线下的线性代数,平时将彻底没有附加的课程压力。阅读讲义还可以深入体验到一种更精细的别致体系,到处掺杂着矩阵分析技术。这一来A2空间部分就是转换叙述的矩阵部分+无穷维。其中无穷维的内容很有些无关直觉的例子,常常要拿几个特定线性空间套进去看产生反例与否,万幸不会作为考察点。课程唯一的压力来源于新茂亲自改卷落拓不羁,以至能够生产均匀分布的卷面分数,但也有3:7后统一调分。总之很适合叠课或水必修,想要精进技巧也有电子版讲义习题练手。
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:很多
wxm讲课水平不错,逻辑性比较强(前提是你得认真听)。听了一学期空间理论,与上学期的矩阵理论对照着去理解,收获不少。wxm的教学方式有不少人评价过了,个人认为其优点是能较好地体现出矩阵理论和空间理论各自之美(矩阵的技巧,标准型主义;空间语言之严谨、条理性)。但缺点也很明显,缺乏了讲二者之间的联系。
期末隔壁班老师出的牛马卷子,不想过多评价。考了四十多分(均分50左右),万念俱灰。但是没想到被wxm捞到了3.3。wxm捞人力度还是可以的。
- 课程难度:中等
- 作业多少:中等
- 给分好坏:一般
- 收获大小:一般
- 难度:中等
- 作业:中等
- 给分:一般
- 收获:一般
上课非常认真,作业要求也非常低,很适合摆烂的同学,上学期给分非常好,希望这学期能保持
- 课程难度:简单
- 作业多少:很少
- 给分好坏:一般
- 收获大小:一般
- 难度:简单
- 作业:很少
- 给分:一般
- 收获:一般
王新茂老师水平很高,他的讲义详细到可以让人不用上课都能自行速成(bushi),从矩阵到空间都有一个相对完备且可以做题的体系。相比上一学期的高强度高难度来说下学期的课程难度低了很多,以至于甚至最后有三个星期的时间没有上课。最后期末考试和隔壁班联考直接把我坑死,和讲义平时的出题风格完全不同导致暴毙
- 课程难度:简单
- 作业多少:中等
- 给分好坏:超好
- 收获大小:没有
- 难度:简单
- 作业:中等
- 给分:超好
- 收获:没有
实际上一个学期没讲多少东西,期末考试考的东西和这学期学的也没什么关系,甚至考线代A1作业的原题,属实是绷不住了,卷面分直接爆炸。。。还好老师给分比较好
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:一般
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:一般
从逻辑的中间插进去开始写评价吧
如果你上学期学的是王新茂,那建议还是接着选下去
纵使上学期你可能被他的难题蹂躏得体无完肤,但这件事和你这学期学的东西又有多大的关系呢?你如果想偷懒不想复习,只需要建立一点观念:上学期的矩阵知识主要来源于定义和技巧,而那些和他这学期所要讲的空间关系并不大(表面上是的)。你只需要留下这个观念,在偶尔需要的地方翻回去找找之前的结论即可,这些就是王新茂的空间语言和上学期矩阵知识的唯一一点联系。
但是你如果上学期选了鑫茂,这学期可以说是几乎必须要选他。众所周知,他讲课的时候把矩阵和空间完全割裂,大概率和另一个班顺序不一样。你如果换班就很可能漏掉许多应该知道的东西。而这学期说实话他的题目并没有上学期那么变态。上课一定认真记笔记,理解每一个定义和定理。他讲义上定理的推导至少要看会,然后即使作业不算分也最好把作业题全做了。其实那些题也基本上都是玩定义,偶尔几个特别难的懒得想了就问人吧。
虽然表面上他讲的顺序是矩阵和空间完全割裂,但其实他就像给了你两个电极。它们之间怎么通电产生火花那就是你的任务,革命没有结束不是吗?比如把矩阵看成线性变换的描述,用特征子空间分解可以直接弄出若当标准型,或是一些矩阵里的结论弄到线性映射之类的,他上课只会强调定义,而思考矩阵空间之间的联系那是你的任务。
似乎是期中期末37开。我期末有幸考炸了,也算是被鑫茂按名次给分的做法捞了一下
- 课程难度:中等
- 作业多少:中等
- 给分好坏:一般
- 收获大小:一般
- 难度:中等
- 作业:中等
- 给分:一般
- 收获:一般
王老师人还是很好的……具有一种洒脱气质。
值得吐槽的是和隔壁叶老师班的蜜汁进度。上学期直接干到正定,结果这学期只有空间,到最后基本上大家全在摸鱼,其实还挺舒服))但是期末统考把王班人干傻了,奇异值分解什么的基本上大部分人都想不起来。
不知道以后要怎么干。
给分……别人都说好,但是我被卡了两个学期,确实是因为自己拉可是也说不出来什么别的了吧)))
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:很多
之前很抗拒上茂爷的课的,毕竟疫情期间网课效果确实一般。结果真正到了课堂,我发现老师貌似之前在划水?讲的很清晰,重点突出,思路也很好,板书也很漂亮,而且非常愿意给同学讲东西,有任何问题直接问老师,老师都会耐心解答,甚至下课呆了快半小时才走,但态度一直非常好。考试的话是期中期末37开+15分平时分,调分力度我认为很大了。我觉得期中很难,毕竟老师自命题,均分只有41,期末陈老师出卷比较基础,我期末复习直接把李书后两章过了一遍,感觉还是挺有用的。出分后老师总评忘给我加平时分了,发邮件联系老师很快就解决了,(虽然教秘拖了三天才修改),但老师确实十分认真负责,出了总评还能让我改分真的十分感动。整体线代A2要比1简单不少,茂爷讲义尽量做,李书看看夯实基础,我觉得是个不错的学习方法。我觉得大家可以放心选茂爷的课,是个好老师!
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:很多
很久没有遇到讲课水平高,给分还这么好的老师了5555 生活不易 憨憨叹气
- 课程难度:中等
- 作业多少:很多
- 给分好坏:超好
- 收获大小:一般
- 难度:中等
- 作业:很多
- 给分:超好
- 收获:一般
这学期紧接上学期疫情,前一个月复习了一下,然后从第六章讲起,矩阵和后面空间理论对应,期中说好不为难大家结果平均分41,查卷时候老师很严厉,过程太菜想加回来,10分一分也没给,但是心服口服,自己写的确实不够好,期末隔壁班出题,记住把李书上面好好看看,隔壁班陈老师会出书上原题,期末很简单,总的下来好好学,两本书结合看,收获会不少。 给分超好,入股不亏(✪▽✪)!
- 课程难度:中等
- 作业多少:中等
- 给分好坏:一般
- 收获大小:一般
- 难度:中等
- 作业:中等
- 给分:一般
- 收获:一般
A2基本不调分或者是优秀以下不调分吧,习题建议全做,或者讲义最起码都看一遍 真的建议能及时并有能力发出习题答案讲义的学长学姐来做助教,就这样,嗯
- 课程难度:简单
- 作业多少:很少
- 给分好坏:超好
- 收获大小:没有
- 难度:简单
- 作业:很少
- 给分:超好
- 收获:没有
这边就是上面提到的55+37=3.3的那位,来报到了()
本学期由于一些原因没学数学,居然能被茂爷捞到这个分数,无所谓了哈哈。
确实非常适合摆子开水,可惜我并没能在王的课堂上学会线性代数——倒不如说妮可目前A系列线性代数整个是混乱的,几乎没有一个正经老师,期末更是经典的整本书内容,并不便于备考。
如果想学,建议还是自己去网上找点资源。