2025秋 2024秋 2023秋 2022秋 2021秋 2019秋 2018秋 2017秋 课程号:MATH100301
- 课程难度:中等
- 作业多少:很少
- 给分好坏:一般
- 收获大小:一般
| 选课类别:计划内与自由选修 | 教学类型:理论课 |
| 课程类别:本科计划内课程 | 开课单位:数学科学学院 |
| 课程层次:通修 | 学分:4.0 |
课程大纲:
数项级数, 函数列与函数项级数, 反常积分, Fourier分析, 含参变量积分.
教材:
《数学分析教程》下册 第3版 常庚哲、史济怀.
考试形式:
闭卷.
教学水平与课程内容
左达峰老师的《数学分析(A3)》课程讲解清晰且结构严密,教学上灵活不拘泥教材,且会补充有趣的题目和小故事,课堂气氛较为轻松。在课程结构上,内容分为无穷级数、反常积分,以及基础Fourier分析三大部分,老师将课本顺序稍作调整,内容衔接自然。A3相比A1和A2稍微简单,但仍需注意内容的技巧性,尤其是在判别法以及函数列的一致收敛等方面。
考试与作业
课程有期中和期末考试,题目难度适中,但对计算要求较高,许多学生认为期中较简单而期末相对更加考验计算与运用技能。平时作业量不大,多为书本上的题目,主要考察学生对收敛性判别法的理解和应用。期中和期末考试成绩都占较大比例,评估相对体现学生平时积累和最终综合能力。
给分
在给分方面,左老师被认为较为公正,用较为客观的比例(如3:3:4的分数设置),很多同学从中受益。对于优秀率的控制比较中庸,期末考试可能作为调节评估平衡的手段。
其他建议
尽管课程整体评价良好,但部分学生反馈对于平时积极性影响的事件(如偶尔的点名和期中成绩公布时间)使得学习体验有所下降。对于想要取得高分的学生,建议在日常作业中重视概念理解和判别法技巧运用,课程间穿插计算练习能显著提高成绩。由于涉及内容基础广泛,建议预习相关复分析知识以拓展理解深度。
总体评价
左达峰老师的《数学分析(A3)》课程受到广泛好评,既适合想要进一步加深数学基础的学生,也适合作为选修轻松课程之选。这门课不仅能帮助学生巩固数学分析中的关键知识,也为后续相关课程打下良好基础。
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:很多
左达峰为什么是神?
在谈论这个问题之前,我想先说说其他老师相较于左达峰究竟差在了哪里。
首先是犯下傲慢之罪的wxm
“空间只能用来吹吹nb,真办事儿还得靠矩阵”,这种傲慢的老师注定走不长远,事实也是如此,靠着一本阴间难度的讲义赢了神之后一直在走下坡路,最终迫使不计其数的学生润到了隔壁。与之相比神就很谦卑,典型的例题,简易的期末都是神留给凡人的慈悲。神不是不会,只是不想通过太完美的表现让对手绝望所以故意不用,可笑有些人不理解神的良苦用心,竟然还用这些事来讥讽神,我劝你们好自为之。
然后是犯下愤怒之罪的mj
因为有学生认为组合学是奇技淫巧就愤愤不平,有人提到神的作业不用打\(\LaTeX\)就怒气冲冲地辩驳,违背了神在《新约》中的一句话:“我觉得当老师就是要能很好地控制自己的情绪吧。”于是神降下了他的惩罚,mj的pksq起火,其言行被嵌入时髦的段子,大家纷纷要求组合退出基数必修。
接着是犯下懒惰之罪的yss
自以为拿下高概的主讲就了不起了,自创几乎延续整个学期的线上授课。另外大家有所不知,其实在jwc公布开课前,yss闭上眼睛做冥想的时候,其脑海中看见的画面,正是站在光芒之中的左达峰,那时神告诉他:“你只可到这里,不可越过。”然而,神的劝说不但没有让yss迷途知返,竟然还敢在期中考伙同wsh正面挑战神的尊严,于是神降下了他的惩罚,yss还没结课便身败名裂,课上的测度论没人记得,从此成为了管院高钙的一大叠课申请理由。
再然后是犯下了嫉妒之罪fxm
屡次被神击败,但口服心不服的fxm,暗中嫉妒着神,甚至胆敢说出“如果大家都学得扎实,反向调分或许更好”这种话。于是,在含金量最高期末考试,即总评的计算上,fxm被神正面击溃。不过,念在fxm最终皈依了神的教,并且践行神的意志讨伐了jwc的逆天规定后,神应许了他在计算方法的一切。
犯下贪婪之罪的hs
只是初出茅庐,hs就夺得了Princeton的PhD,而这,自然是因为神的应允。神本来钦定他为自己在数分(B3)的代言人,在自己退役之后替自己继续讨伐数分(A3)的理论,为此甚至不惜亲自为hs铺路,将一切荣耀都归给他,甚至应允他可以带走自己最爱的史书。但最后hs却被利益蒙蔽了双眼,不再以践行神的理想为自己的理想,也不再聆听神的教诲,甚至自以荣光已经超过了神,竟允许学生P出“我B系列都讲流形上的微积分了,你呢?”这种亵渎神尊严的图片,于是神降下了惩罚,hs从此不再人称奶爸并且拥有一个醒目的绰号“胡分析”,而他的讲课将再也不能独自carry,他的习题再也不能强势压制对手,他的考试将再也不能开团,他的给分也再不能替他揽下大锅,吸收火力。
犯下暴食之罪的zlf
在神子hs堕落之后,神开始寻找下一个代言人,这一次,他选中了zlf。相较于神,zlf无疑是不完美的,他没有神足以让学生追捧的亲和力,也没有神游刃有余的课时安排,给4和4.3的胆气,敏锐的选教材嗅觉,无懈可击的证明,但神将自己最虔诚,同时也是实力最强大的两门课程(微分方程Ⅰ和Ⅱ)暂时交给了他,但由于数分(A2)一月一小测的事,神认为或许是自己给的压力过大才导致了神子的堕落,于是这一次神选择了在微分方程期中考前拿一整节的课上时间给学生复习,减少zlf的心理负担,最终,zlf成功了。然而,期中考完后的zlf不但冒大不韪在习题课上使用了签到,更在最终计算总评克扣了大量4+,只是他错误地认为神的力量来源于增加课堂容量和习题课,最终他也因此犯下了暴食之罪,并在23春无缘微分方程Ⅱ。
最后,犯下淫欲之罪的cxw
疫情封校之后,神已经非常虚弱了,ustc用jwc吸走了神的精气,神已经无力再惩罚zlf,只有信徒依旧在维护神的威严而已。此刻已经决心退隐的神在最后依然心系数院,于是他选中了第三位神子——cxw。作为第三任神子,cxw好地维护了神的威严,但在接连带了好几届H后,cxw遇到了syh,被吸走了神赋予自己的“H课不限优秀率”,于是在给分中连连失误,最终葬送一批提前选课的大一佬。
上半部分我们谈了其他老师相较于神的不足之处以及他们犯下的“罪行”,现在我们来谈谈神为什么是神,神为什么凌驾于其他老师之上,以及在他身上究竟有哪些美德值得我们去选课。
首先是神的忠诚
众做周知,《数学分析教程》是一部极其优质的数分教材,它是前代神史济怀先生的为信徒留下的圣经。纵使神至高无上,神依然忠于史书,没有贸然编写使用新的教材。神真正体恤学生的苦衷,参考史书传道授业,精选了其上的例题以指点迷津,又在讲授中无处不纳入神的思想与创新。神忠于圣经,存异而不逾矩,这便是神之所以成为神。翘掉神的课堂,实在是对神极大的不敬。
然后是神的节制
神在A卷取消之后,因繁忙的行政事务而不慎染上了恶疾,原本神可以继续享用他因病弃课的权力,但神在看到老中青三代神子接连堕落之后,终于明白,Fourier必须由自己亲手拿下。为了履行天职,神竟然用手写板继续上课,我想大家都很清楚连着在手写板上写两节课字的滋味,尤其是对于常年板书神来说,这更是无法忍受的,但神忍耐了下来,并且坚持了下来,这就是神独特于他人的“节制”!
神的慷慨
我们都知道,全科大的老师都以完成教学任务为自己的最终目标,但他们往往难以达成愿望,乃至于最后成为心魔,不是泯然众人,就是变得疯疯癫癫。神是慷慨的,他愿意将自己的课堂的一部分让渡给学生和其他老师。甚至写下大部分例题后,都会留给学生长达5~10分钟的时间思考讨论,自己宁可讲得紧凑一点,而不是忽略知识接收速度地直接向学生灌输。这就是神的慷慨!
神的勤奋
神一生反抗屑课,从未停歇,但体恤学生终究不是一件简单的事,不光是大物实验,在量子物理项目上,亦要抗jwc!神之所以是神,就是在jwc副主任任上他敢为天下先,勇于承担责任!调回数院工作后,意图开辟新战场,继续与jwc一决雌雄的神,在其他老师都已经休息的时候,带领他忠心的仆从们彻夜讨论改革方案,这便是神的勤奋!
神的温和
回到学院工作之后,部分不够沉稳的信徒竟因为在网上随意发表言论背刺了神,更用本属于神的职责困住了神,使得神8点游完泳便要去与信徒“喝茶”,甚至10点才吃了晚饭。这种卑鄙无耻的背叛行为放在任何一个人的身上,只怕都要“长篇大论,说教不停”,但神没有,神甚至在自己最愤怒的时候,也只是以理服人“上网的时候不要随便发表一些言论,你们说的话都是能查到的,不要觉得几个人的qq群说几句话就没事”,这便是神的温和!
神的谦逊
大家都知道,相较于其他老师,神拥有深不见底的数学功底,除了数学分析,就连微分几何,调和分析,量子场论也都是神的拿手好戏,更不要说神可怕的科研压制力,甚至拿下PhD后直接受邀留校,并不需要找工作。除此之外还有无懈可击的谈吐能力,遥遥领先的调分能力,脚本般的思路推导,这样的神,完全可以欣然接受世人膜拜。但神没有,提交了总评之后神只公布了调分公式,尽一切可能给优秀、捞卡绩,而直接解散课程群,避免学生在复读认爹上浪费时间,这就是神的谦逊!
神的节俭
这里就要说说经常被黑子们提起的作业一事了,其实真实情况与大家想象中的大相径庭。大家都知道,作业是一项很浪费学生精力和时间的事情,节俭的神自然不会这么铺张浪费。之所以神会只选择两三道习题当成作业,其实是因为神看到电磁学、大物实验报告等极其令人不快的事物,不想浪费学生时间的神准备减少课后负担才布置极少的作业,在ddl漫天的年代,这样的神怎么能不被大家爱戴呢?
(以上文字纯属整活,没有恶意拉踩老师之意)
2023年7月14日 10:50分
左老师回复了我的助教申请邮件:“我这边至多只有一个助教名额给本科生。”
最初打算与同级的一位巨佬一起应聘,由于只剩一个岗位,我的总评压线95,竞争力远不及那位佬。于是体面退出。
我一介凡人,果然配不上神的崇高啊......
- 课程难度:简单
- 作业多少:很少
- 给分好坏:一般
- 收获大小:一般
- 难度:简单
- 作业:很少
- 给分:一般
- 收获:一般
一年半的数分学期在今天算是画上了句号, 在这里把苯人对数分3, 还有数分的一些想法胡乱说一下吧.
先说说这门课吧.
虽然苯人不太爱听课, 但是从苯人极为有限的听课时间看来, 左老师讲的还是挺不错的:
- 上课会补充一些书上正文内没有(甚至书上也没有)的题目, 里面的一些小trick或者想法还是有助于加深对数分的理解的(有些题目初见的时候还是有点杀的, 苯人这种菜鸟经常反应不过来hhh
- 左老师上课不是完全按照书来讲的, 讲课的顺序不少地方和书上不同, 也会讲解一下自己这样处理的思路. 虽然这样会导致苯人不听课就不知道班上学到哪里了, 但是看板书过一遍+看书过一遍的体验是很有趣的. 毕竟书本不是什么权威(sjh要再版了, 上面的少量内容也有点小错), 老师有一些证明我认为是挺有启发性的.
- 老师上课的时候会分享一些小故事, 适合苯人这种爱听故事的(憋笑)
至于作业, 左老师的作业好像是比隔壁班少的; 关于助教, 这个学期某位助教把课程群的群等级全改成了原神的地名hhh, 不过两位助教人还挺好的hhh(srds助教是会变动的hhh)
关于参考书, 苯人觉得sjh这本书上的题目已经够多了, 上面的例题和习题问题基本能覆盖这门课的考试题目, 而且老师上课也补充了一些题目, 题是做不完的… 个人觉得还要再看的话, 就看看Stein的Fourier Analysis吧. 这本书的可读性挺强的, 并且是在Riemann可积函数的框架下做的, 所以不太需要什么额外的知识(而且苯人感觉很多往年卷的有趣题目都是这上面的topic, 比如Weyl distribution和Poisson formula…)
给分啥的, 下次再说吧hhh
最后说说数分吧, 数分三学期, 苯人感觉每个学期都各有侧重, A1是一些逐点估计(用微分工具, 以及114514个神秘小技巧), A2是大量的计算(如学的欧氏拓扑, 以及没有引入鸡肋Jordan outer content的模糊处理, 主旋律还是计算), A3的整体估计(想想一致性, 或许该说是分段估计?). 其中, 苯人最喜欢的就是分段估计了hhh

真的, 每次把积分啥的切成几段, 然后挨个说这个啥时候小, 那个啥时候小, 就有一种度长絜大的莫名喜感()
课本上很多定理的处理是和上下文有关or打包的比较简洁的, 但是出于个人喜好, 苯人把大量的定理都按上面的模式自己重新走了一遍, 感觉还是很好玩的, 虽然没有什么fancy的玩意, 但是朴素的东西也能让人快乐呐
当然, 数分不是一个太朴素的家伙, 里面还有一些颇有背景的trick. 比如, 在学A3的时候, 有个题目的技巧一开始让我有种从天而降的难绷感, 直到苯人在拓扑课学到了AA定理, 才get到那个技巧的大意, 颇有种蓦然回首, 那人却在, 灯火阑珊处的感觉. 所以学数分技巧, 去学后继的一些课程也是一条可行路子(?)
不知道这课为什么今天才出期末成绩… 隔壁班总评都出了…

公式如图, 看起来和隔壁班用的公式差不多? 会赢吗
补更: 左老师确实一分没调, 不签到也真的会向下调分hhh
- 课程难度:简单
- 作业多少:很少
- 给分好坏:超好
- 收获大小:一般
- 难度:简单
- 作业:很少
- 给分:超好
- 收获:一般
左老师真的有大师风范,感觉是很潇洒的那种气质,讲课感觉信手拈来的熟练,还会穿插聊一些他的轶事,课堂很轻松,而且A3本身应该也比前两个数分简单一些,一学期下来也没投入多少时间,适合学其他数学课类了的时候换换脑子()?最后成绩也还可以,考试也不难。
又一个95!左老师你带我走吧😭😭😭你是我叠!
- 课程难度:简单
- 作业多少:很少
- 给分好坏:一般
- 收获大小:一般
- 难度:简单
- 作业:很少
- 给分:一般
- 收获:一般
这是数学分析系列课程的终章。
上课内容为常庚哲,史济怀《数学分析教程》的14-18章 五章内容可以分为三个部分:无穷级数(包含数项级数和函数项级数)反常积分(含参/不含参)和基础的Fourier分析。这其中,无穷级数的内容和反常积分的内容可以用离散v.s.连续的观点对偶起来,其中的许多性质和判别法都是平行的;而Fourier分析部分分为Fourier级数和Fourier积分,可以说是对前两部分内容的应用,但实际学习的体验其实只有如同数分A1的积分计算。
因此,左老师按无穷级数(ch.14 15)→Fourier分析(ch.17)→反常积分(ch.16)→含参变量积分(ch.18)的顺序来上课,与正常的顺序相比也并没有什么不足。
左老师上课沉稳,课堂上会举不少例子(能占到30%+的课堂内容),我认为是比较合适的,当然这也与这门课内容确实比较少有关。
作业不太多,基本都是史书练习题,网上能找到答案,但是不建议抄,这本书课后习题的质量在14-18这几章达到了巅峰,如果全部掌握,应对考试绝对没有问题,不需要另外刷题。(其实整个数分A系列课程都是这样)
这门课的内容少,难度偏易,导致两个课堂的到课率都不算太高,老师对此是比较气愤的,好几次课都为此发过脾气,并于某次课上进行了点名性质的小测(只有一道题,老师讲解完才收的,也可以直接抄书后答案)。
有期中和期末,期中只考了无穷级数部分,考的很简单,均分八十多,期末估计要下狠手,害怕。
期末考完upd:感觉期末也没有下狠手,一份很常规的卷子,不会要向下调分吧
回旋镖来的如此之快,期末计算算错翻大车,寄了,奉劝后来者重视计算。
总评已出,按235算出来多少就是多少,没调分。
- 课程难度:中等
- 作业多少:中等
- 给分好坏:一般
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:一般
- 收获:很多
出分了,89(均分66)+85(均分64)=91,似乎235之后调了几分。不知道其他分段有没有捞一手,如果严格235的话总评似乎会比较凄凉
目前还没出总评,先占个坑。
左老师上课水平很高,给人以一种老艺术家的从容,上课的时候还会时不时来点“思想教育”(比如多次让同学们来上课)。很喜欢老师在课上可以留出时间讲例题并且留给大家一些时间思考,让我一个数学水平不高的同学也能跟上课堂节奏。整体来说A3的难度确实远低于A1和A2,没有很多奇怪的技巧,感觉就是把式子分几段然后估计一下,所以课下也没有特别去花时间(相比于隔壁的PDE和wxm的神秘线性代数)
不过今年的试卷似乎和往年卷风格迥异,难度远超往年卷,难道是因为之前的评课都说数分A3太水,今年开始要上强度了吗,那我只能说xdx们有福了……
- 课程难度:简单
- 作业多少:很少
- 给分好坏:超好
- 收获大小:一般
- 难度:简单
- 作业:很少
- 给分:超好
- 收获:一般
左老师上课讲的很好,基本都能听得下去而且听的很轻松。(可能是淑芬A3本来就不是很难)
左老师非常好,在助教改完试卷后会把所有试卷看一遍。
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:一般
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:一般
本人是2023秋数学分析A3左老师的的助教,先来占坑。
数学分析A3这门课有以下特点:
1、工具性强
从数学对象来看:数项级数,函数列,幂级数,广义积分,傅里叶级数和含参变量积分,再细化一些的话还包含Fourier变换,Gamma函数,Beta函数(当然这三个貌似不是教学重点,但可以作为大二下复分析H的部分前置知识)。这些数学对象基本都是为了以后实分析,复分析,微分方程等课程服务,给我们提供看待光滑/全纯函数(函数的幂级数展开),某些特殊的微分方程(如热方程的Fourier变换解法)的一些新的角度,又或者是提供离散测度Fubini定理的大量鲜活例子,本身没有太多可以挖掘的地方。
从学习重点来看:重点之一是各种判别法的运用,包括比较判别法,Cauchy,Dirichlet,Abel判别法,一致收敛的Weierstrass判别法,这些判别法的学习和运用将贯彻整个数学分析A3,串联几乎每一个上面提到的数学对象。打个可能不太恰当的比方,这门课相当一部分时间是在学习“如何熟练运用一系列的方法,工具,来说明级数/积分这个工具的某些较好的性质”。另一个重点是一个概念:一致收敛。一致收敛在数学分析A3的函数列,幂级数,含参变量积分均有提及,笔者在这里将其概括为“工具”,是因为一致收敛的函数列/幂级数具有相当好的性质,为我们研究函数提供一个非常优秀的框架(框架打太大容易无从下手,这点有兴趣修读任爷实分析H可以进一步品味体会)。在这个框架里,某些良好的性质得到“继承”(如:连续,可积,可导),某些理想的计算方式得到实现(如:极限,积分,求导的交换性)。而幂级数是契合这个框架的优良数学对象,对幂级数内闭一致收敛的运用,将在实分析和复分析中发挥重大作用。
2、可类比性强
从级数-积分角度:数项级数对应广义积分,函数列对应含参变量积分,前者可以看成后者的离散测度情形(或者可以理解成把离散的n换成了连续的x),后者可以拆分成前者(也就是积分限的拆分)。因此级数的判别法,在积分里面基本有对应的方法。
从数项级数-函数项级数角度:当函数项级数的变量x固定时便是数项级数,因此函数项级数可以看成“一族数项级数”,级数收敛性研究单个级数,而研究一族数项级数时,整体的表现将比单个的表现更有价值,由此诞生“一致收敛”。从个体到整体的变化,会让判别法产生一些区别,但常用的Cauchy,Dirichlet,Abel判别法大体保持了继承。广义积分-含参变量积分同理。
从实级数-复级数角度:在复分析的学习中,同样会引入复值级数,复变复值函数列,当中的判别法也基本继承自数学分析A3所学。
3、可水性强
3、相对轻松
从课堂教学来看:老师基本稳定一次课上教材一节内容,有时候一节课两节,但绝对不会让大家感到讲得很仓促。老师上课非常从容,课前会讲点小故事(可能涉及学校最近发生的事情),课上没讲完一个定理证明会停下来询问大家有没有什么问题和建议,会布置课上练习(不是小测,只是老师讲例题之前给大家时间思考),有时候还会用正课时间上习题课,教学内容之少可见一斑。
从作业布置来看:作业量少,大部分是收敛判别法运用的题目,外加一道课后习题中的证明题,偶尔布置节后的问题,或者自己在黑板写一道题留成作业。每次布置的作业,对笔者来说,用下课吃完午饭回宿舍之后的半个小时内可以写完,根据笔者的水平,相信班上有很多同学也是如此。而且由于众所周知的教材有完整答案的事实,想写不完实在是件十分困难的事情(bushi)。
从考试难度来看:数学分析A3的命题是两个班的老师一起命题的。左老师也在课上反复强调:“要有一定的区分度”,“精准把控平均分”,“想要上85可能需要一点实力,想要上90可能还需要一点实力”。从2022秋期中考试来看,前面4道题是十分基础计算或者定理直接运用;第5题考察相对复杂一点的幂级数展开计算;第6题是课上例题,第7题考察一致逼近;但是需要做奇函数延拓,不过不难想;第8题笔者水平有限,未能做出,不过写点思路想法或许可以拿点分。从期末考试来看,由于特殊原因,是开学考,因此卷子也出得十分简单,除了最后一题是教材问题原题证明题外,其他都是计算题,因此高分很多,满分也有好几个。总的来说考试题目偏向计算,证明有区分度,但大部分题目都能在课上或者作业找到原型,老师不会出偏题怪题为难大家。
从给分来看:2022年秋给分是平时:期中:期末=3:3:4,优秀率是39.8%,而且尽量不卡绩(优秀附近似乎由于优秀率限制的原因确实没办法),老师是知道有评课社区的,也知道大家的需求。
一些小小建议
1、只做作业可能不太够
从熟练度来看:对各种判别法的熟练运用是这门课程考察的重点,如果觉得做了作业还是对判别法运用比较生疏的同学,可能需要增加练习。笔者认为教材上面在这方面的题量是足够的。
从分析能力来看:老师布置的作业中证明的占比比较少,因此对大家的分析能力的训练较少。若是想在考试中冲击更高的分数,建议认真消化课本定理证明,学有余力的可以做做教材后面的问题。
2、不建议在这门课上花太多时间
大二上学期三门数学课,在笔者看来数学分析A3远比其他两门课要轻松得多,要打数理基础也是往线性代数A2和微分方程引论那里打啊。当然也可以提前学习自己感兴趣的以后的课程,提前学习大二下学期的实分析,复分析课程,还可以让老师加快进度讲完数分A3内容然后开“流形上的微积分”(bushi)。
----------------------------------------------------------------------------------------------------------------------------------------
老师今年调整了讲课顺序,先将14-15章,这也是期中考试内容。然后直接讲17章(Fourier),再回过头来讲16和18章,期末考试内容则是16-18章。
期中考试整体容易,由大概10位同学提前交卷,最终班上平均分82.8,中位数88,满分的也不少。期中出分后老师在群里明确期末考试难度将会加大(
期末考试难度比期中考试要大很多,不过难点基本都在数分A1上。比如第一题(5)要证明Riemann可积函数可以被连续函数在L1范数下逼近,第4题(2)计算极限需要使用洛必达法则,第6题的其中一种解法(也是考场上大多数同学的做法)是利用可积性理论分析,让人有种在考数分A1的错觉。期末总体情况感觉上是符合老师预期,起到了跟期中均分“拉扯”的作用。但老师要求助教期末不能公布均分与分布,所以就点到为止吧。
在给学生查完卷之后,笔者的助教工作大概也结束了,剩下的事情,包括查卷之后的加分复核,后续的分数调整和给总评,都是由老师来完成,作为助教什么都不知道。不过好像这次期末改卷第六题(本人改的)放水过于严重了,老师要重新看看,不清楚会不会出现个别同学期末分数下调。
最后上传了一些课程资料,写讲义真的太辛苦辣!
- 课程难度:中等
- 作业多少:中等
- 给分好坏:一般
- 收获大小:一般
- 难度:中等
- 作业:中等
- 给分:一般
- 收获:一般
数分A3(和数分A2一起)应该数院唯二两门大水课了
zdf上课中规中矩,基本按照课本,除了傅里叶分析挪到了最后讲,会讲不少例题(也看得出来数分A3确实内容少)
整个学期老师点了一次名,据说是用来捞优秀率和捞卡绩用的
一个很有意思的特点是zdf非常喜欢“劝学”,经常说一些“至理名言”,看得出来苦口婆心:
- 你们缺的不是能力,是态度!
- 数分B2有一年期末考,四十多个0分,一问,都战略性放弃了,在试卷上签个名下个学期补考吧
- 我今天有点想小测,不过有点失人品,算了
- 一本教材如果出了参考答案,那么它就废了
- 前天评少院郭沫若奖学金,竞争很激烈呀。其中有一对双胞胎,哥哥4.18,妹妹4.16
- 你们求导都退回到高二的水平了
- 你们计算能力还是不行,怎么傅里叶系数都算不对
- 最后我们的学生变成四不像了,算数不会算,证明又不会证
- 你们寝室味道这么大,不来上课,呆寝室吗?
- 试卷不能出太简单,不能把科大数理基础丢了
- PDE刚刚学就觉得困难呀?
贴一些考试数据,供来者参考:
期中考:
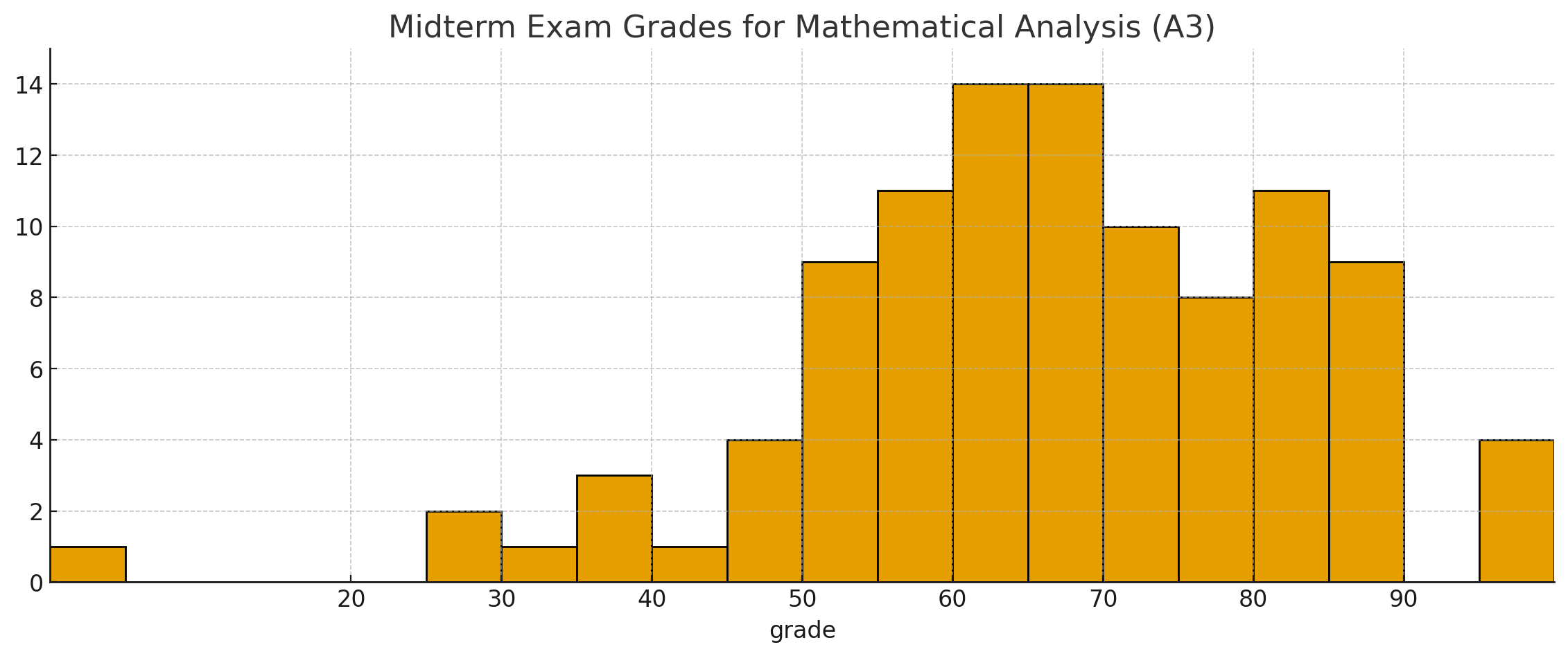
期末考各题平均数:

- 课程难度:中等
- 作业多少:中等
- 给分好坏:一般
- 收获大小:一般
- 难度:中等
- 作业:中等
- 给分:一般
- 收获:一般
我觉得这门课让我挺难受的,首先是期中,助教晚上十二点在群里面@全体成员发成绩到bb,刚要睡又被逼着从床上下来打开电脑查看成绩,成绩自然是没考好(谢惠民上原题是计算题,答案并没有详细的边计算边证明你为什么这样算是对的这种细节过程,误认为这是一道计算题(其实计算量也不小),导致12分的题目被扣了8分),晚上自然是睡不着的,第二天戏剧性的一幕出现了,早八课堂本学期唯一的一次签到,用来捞卡绩的,自然是没有把握住,这严重挫伤了我学习这门课的积极性。其次是真就一分都不会调,235or244取高的那个,个人认为期中比期末简单不少,这意味着期中考炸的很难在期末翻盘。虽然最后狗运没有被卡绩,但从学期初到学期末学习这门课的积极性严格单调递减。
- 课程难度:困难
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:中等
- 给分:超好
- 收获:很多
给zdf打个十分
但是希望大家以鼠鼠为戒,不要真的把这个A3当成水课🤡
你瞧不起A3,其真的有可能瞧不起你🤡
期末对完答案连连爆扣 已经预订目前数学最低G了
- 课程难度:困难
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:中等
- 给分:超好
- 收获:很多
先分享下考题
崩溃了,内容简单奈何一眼出的东西一错再错白扔几十分…
A3能写成这样感觉即将到来的线代和方程也要没了…什么时候才能学会数学呀
提供低分段样本:期中期末均67。期中平均分七十多一点,期末隔壁班平均65,这边没公布,应该会高一些吧。总评75
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:很多
期中出的比隔壁班快,感觉卷子是一如既往的水,但是架不住本人接连两个究极唐氏错误被爆杀低于平均分😭已经准备重修了😴
- 课程难度:中等
- 作业多少:很少
- 给分好坏:一般
- 收获大小:一般
- 难度:中等
- 作业:很少
- 给分:一般
- 收获:一般
即使是从我去过的为数不多的课也能感觉到左老师讲的真的很好,没去多听几次课真的是很遗憾。作业留的不多,而且似乎质量挺高。考试难度无法评价,调分方式不太清楚,但老师捞及格的力度相当之大,绝赞好评!(但数分A3的内容我是真的不喜欢,而且东西真的非常多,学的时候身心俱疲,无比痛苦,所以扣一分(x)
- 课程难度:中等
- 作业多少:中等
- 给分好坏:一般
- 收获大小:一般
- 难度:中等
- 作业:中等
- 给分:一般
- 收获:一般
占个坑,这学期助教非常认真负责
期中upd:终于知道老师长啥样了,不得不说作业和考试内容的设置很不错,基本上作业全做一遍考试就都能写了
期末upd:总评被杀了呜呜,期中98+期末70等于寄,但这个应该说不怪老师,期末的难度是很友好的,是我第一大题-20太唐氏了
评分9->4 原因是下半学期的一次点名
- 课程难度:简单
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:简单
- 作业:很少
- 给分:超好
- 收获:很多
左达峰就是神,另外奉劝同学们不要翻墙,否则左老师很快就到你家门口(不是)
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:很多
老师给分超好的,期末卷出简单了临时改了总评公式,而且不卡绩,88.9-89-90。不过总评公式一改,平时分少了,对低分段就不太友好了。
老师上课非常清楚,速度适中,节奏把握的非常好。除了书上的内容还会补充一些,学下来收获非常大。
- 课程难度:简单
- 作业多少:很少
- 给分好坏:超好
- 收获大小:一般
- 难度:简单
- 作业:很少
- 给分:超好
- 收获:一般
出分了来评价一波。首先左老师上课很好,上课基本都是书上的内容,偶然有点Stein和谢惠明上的内容。课前会大概回顾一下上节课的内容和接下来要做的事情。证明也都是先讲思路,然后完善细节。课间还会和我们交流分享有意思的事情。不点名。不过虽然给了我4.3,我还是想吐槽一下期末考试。(前90分白给,最后一题太难。。能不能把倒数第二题出难点,最后一题简单一点。)总之,强烈推荐左老师!
- 课程难度:简单
- 作业多少:中等
- 给分好坏:超好
- 收获大小:一般
- 难度:简单
- 作业:中等
- 给分:超好
- 收获:一般
我最后悔的事情就是这个学期上了左老师的课,一想到以后估计没法再听到左老师讲课了,还是有些难受的。
左老师的A3课内容已经有同学梳理过了。他真的很有热情,讲课质量也非常顶,此外两位助教大大也很有耐心。因此虽然pksq挺多人把这门课当成较水的课看待,但我对这门课的态度反而比A1,A2更认真了。我觉得这是目前上过的少有的好课(各个层面上)
如果学有余力的话,很推荐大家读Stein的傅里叶分析,内容丰富了很多,也给出了很多的应用场景。英文原版里很多话写的非常生动,但是翻译过后的版本比较粗糙,甚至有时候看着会犯困。
最后做一个参考吧。期中86,期末84(老师会在查完卷以后重新把所有试卷过一遍),总评可能在4或者4.3(虽然4.3几乎没戏),班级均分在60~65左右。今年的卷子说是比往年难,但是个人考下来觉得还好,主要为自己犯的几个低级计算错误有些小遗憾。插个眼,等出分了再更新。
最后给个9.9分,扣0.1分怕左老师骄傲(doge)四舍五入给到十星
1.15更新
突然记起来左老师这学期有小测,但是他说并不算在成绩里,只是想看看来听课和不听课的人最后的表现。算是把基本的一些情况进行了补充。
早上一看出成绩了,果不其然是4.0,那说明给分确实是严格按照235来的 意料之中,我的数分之旅最终也算画上了句号。
- 课程难度:中等
- 作业多少:中等
- 给分好坏:杀手
- 收获大小:一般
- 难度:中等
- 作业:中等
- 给分:杀手
- 收获:一般
本学期的讲课顺序是级数→函数项序列和函数项级数→广义积分→含参变量积分→Fourier分析。左老师的上课水平相当高,对要讲的内容可谓是信手拈来,并且讲得非常细致易懂。还会讲很多有趣的故事(雾),属实还是比较快乐的。有一次点名性质的小测,作业不多。实际上的内容肯定是没那么难的,如果A1学的好这门课肯定也不会很吃力,但是这学期期中和期末都有一定的难度,有若干CMC难度的问题,想拿高绩还是得稍微花点力气。两位助教从平时作业批改到查卷,都非常认真负责。这当然是值得打十分的课程。
一点小小的建议:Fourier分析的内容讲的确实有点少,感觉Fourier变换这一块完全是在章方程那学的。或许可以考虑把除了这一块的其他内容用半学期上完,然后接下来半个学期结合Stein的书来讲Fourier分析,也许会是一个不错的尝试。
给分应该是235微调or不调,怎么看上去会挂很多人)
- 课程难度:简单
- 作业多少:中等
- 给分好坏:一般
- 收获大小:一般
- 难度:简单
- 作业:中等
- 给分:一般
- 收获:一般
2026.1.30更新
这门课的内容安排有待改革。级数和无穷积分当然需要补充,毕竟这块A1和A2没怎么讲。然而剩下的内容就只有傅里叶级数和一点点傅里叶变换。相关的应用没怎么讲,考试用到的傅里叶级数感觉比较脑筋急转弯。当然做不出来就寄了。
就一学期4学分课而言,目前的内容量还是非常少,跟同时期的4学分微分方程引论对比鲜明。感觉可以学习于品,讲一点点分布,毕竟现在高等实分析的课程已经变得意义不明了,中科大数院学生读完大三上可能都不知道分布是什么。相比于傅里叶级数,可能分布也更适合出题一些。
- 课程难度:中等
- 作业多少:中等
- 给分好坏:一般
- 收获大小:一般
- 难度:中等
- 作业:中等
- 给分:一般
- 收获:一般
晚上十二点多出期中成绩衔接早八签到combo,😅还好我来了。
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:一般
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:一般
课程内容:史书14-18章,其中15章后面的部分似乎不太重要,老师讲的也很简略。16章多重积分不讲。 讲课水平:一个词,游刃有余。左老师上课经常会分享一些有趣的事情,很多都和同学们的生活密切相关。小小的不足是老师的字有些小,有时候来晚了坐后排看不太清。不过自从国庆后被其他几门课杀的昏天黑地也就导致我后面没怎么听过课了。还是那句话,听课是享受,对于数学分析课程而言最好还是能静下心来自己慢慢体悟。而我这学期是没有闲暇去享受听课的。
两位助教都很认真负责。平时问问题李月助教回复的很及时,国庆后有次作业我漏了几道题还专门提醒我比较,实在是大好人。另一位何助教期中期末考前会分享一下自己总结的注意事项,对我很有帮助。
期中期末考试难度都不大。期中考完后均分很高,老师扬言要在期末痛下杀手。但实际上还是心慈手软,出卷较为基础。在仔细阅读教材完成每一道习题后应该是全部都能做出来的,因此不用去刷额外的题。再次提醒同学们由于试题难度不大一定要重视计算的正确性,建议考前算几道题找找感觉。
最后厚不要脸的分享一些我对于A3的学习体悟: 这门课的结构很清晰,前半学期和后半学期的内容应该进行类比。课后题15.3.6很重要,我觉得应该将其视为一个定理。它的结论涉及到极限和级数的交换,与定理18.2.9和18.2.10可以进行类比。它的证明思想也很经典,期中的最后一道题我就是用这个思想解决的。第十八章难度较大,在与级数类比的过程中我产生了一些困惑,想了很久后才明白是十八章的记号有些混乱。在介绍函数极限的一致收敛和后续反常积分的一致收敛时x,u的地位实际上是反过来的。如果大家能把十八章的定理和前面级数部分的定理类比成功,把各种交换性搞明白,那这门课也就学的差不多了。
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:一般
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:一般
老师是好老师,讲得不错,也比较能共情学生。 一切都很好,但是考试出卷风格和A1与A2大不同,计算题居多(利好我这种证明渣),因此难度略有降低,均分显著提高。不过A3想出难一点的证明应该还是能出出来很多的,如果想深入学习数学的除了应付考试也应该自己多去了解一下定理的证明以及背后的动机。不过,这门课想要得高分一定要有扎实的计算力。建议选课。
- 课程难度:困难
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:很少
- 给分:超好
- 收获:很多
数分A3本来应该是非常难的。。。不知道怎么就变成公认水课了。。。可能考试比较简单(也并不是啊。。。 老师人特别特别好,我期中期末都没考好最后去查卷期末一处硬是厚脸皮说扣的分太多了,老师二话不说加了6分,最后总评正好卡住了百分之四十的线(最后一名),QQ上问老师老师还发了个哈哈的表情包,太感动了。。。
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:很多
三学期淑芬课了,一块做个评价吧,感觉这三学期左老师都很照顾我们,平时能关注学习都会尽量关注我们的学习,经常跟我们一块吃饭也会跟我们聊聊一些其他的事情,比如一些做数学做的很好的老师啊什么的,告诉我们一些道理,感觉好到炸裂,最平易近人的老师,上课非常清晰,无奈我这学期上课睡过去比较多,最后反常重积分连上过了我都忘了,好在左老师告诉我不考,最后期末不难,基本上作业题会做就能考85+稍微好好做点题95+没大问题,因为这学期考试比较容易所以基本上算出来多少给了多少,不过老师是按前十名4.3给的, 所以就算比95低一点也还是可以的,万分感谢左老师,奶了我三个学期的淑芬,真的学到了很多,希望以后还可以带我们其他的课!!!资瓷左老师!!
- 课程难度:中等
- 作业多少:很少
- 给分好坏:一般
- 收获大小:一般
- 难度:中等
- 作业:很少
- 给分:一般
- 收获:一般
提供一个低分段调分样本。
平时作业全交,唯一一次点名到了,期中55,期末54。
总评66 1.7。
还是呃,捞了我两分的?
但低分段显然捞的很有限(来自一个被罗罗惯坏的摸鱼人的发言)
zdf老师讲课其实真的很棒,目前在所有数学课里t0级别没问题。数学分析系列是一款我的问题。
- 课程难度:简单
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:简单
- 作业:很少
- 给分:超好
- 收获:很多
学A1时比较摆烂,A2出于某些原因期末炸了,A3终于给数分系列画上一个完美的句号,感谢zdf
老师讲课讲的是很好的,还非常关心学生,会和我们分享很多事情,相当温和
本学期不太好的就是期中出成绩当天早八点名,据说是期中前lsm和zdf聊天时提到的。不确定明年的课还会不会点
- 课程难度:简单
- 作业多少:很少
- 给分好坏:一般
- 收获大小:一般
- 难度:简单
- 作业:很少
- 给分:一般
- 收获:一般
计算总评89.466
挂在这里看看捞不捞
捞了 赢
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:很多
绝对好老师!讲课清晰,主次分明。最印象深刻的点是:课堂上会注意到难点而放慢速度,甚至再过一遍重点来加深大家印象。期末出卷也非常友善,给分很好。
- 课程难度:中等
- 作业多少:很少
- 给分好坏:一般
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:一般
- 收获:很多
期中成绩甚至没到平均分,下半学期改悔之后期末冲一把上了90,感谢左叠把总评捞到90😭
- 课程难度:中等
- 作业多少:中等
- 给分好坏:一般
- 收获大小:一般
- 难度:中等
- 作业:中等
- 给分:一般
- 收获:一般
老师讲课讲的还是很好的,但是上完课总觉得14,15,16,18章似乎就是复制粘贴,老师很喜欢拓展一些谢惠民书上的小结论,总体上课体验感还是很好的。坏处就是:老师提高到课率的方法是向已经到课的同学吐苦水加展示以往极度优秀的学生,大范围攻击,听完有点点亖了,然后希望绩点出其不意地高也是不可能的,老师给分比较科学,希望高绩点建议出门左拐去李班上课()
- 课程难度:困难
- 作业多少:中等
- 给分好坏:杀手
- 收获大小:很多
- 难度:困难
- 作业:中等
- 给分:杀手
- 收获:很多
三个学期的数学分析终于还是在凄凉中结束。
课程内容
正如很多学长说的那样,A3是A系列淑芬里面最具“分析味”的一趴,当然也是相对最简单的。A3的内容包括:数项级数、函数列与函数项级数、反常积分、含参变量积分,还有Fourier分析。之所以这样写而不是按照书上的章节顺序写,是因为左老师上课就是按照这个顺序讲的。从知识的连续性上来讲,讲完函数项级数和反常积分直接讲含参变量积分确实比较好。但是今年左老师的这个讲法给隔壁PDE章班带来了巨大的困扰,因为他们在解方程的时候需要用到Fourier分析的知识。(更好笑的是,Fourier积分的定义有三种,似乎很多同学在这里都被绕晕了hhh)
虽然有这么多章,内容却可以高度凝练。简单来说是级数/积分收敛的各种判别法,最重要的内容是一致收敛的概念,从一致收敛可以得到连续、可导、可积等重要性质,从这些性质又延伸出各式各样的题目。强大学长们已经有完备的总结,这里不再赘述。
关于老师
左老师上课内容基本上都是按照课本的内容来讲,中间穿插一些分析上的内容和注解。整体讲课节奏不快甚至有点偏慢,讲到第17周才结课。部分地方我都认为有点拖了……
左老师不调分这件事在前几个学期亦有记载,只是没想到这个学期老师干了个大的。已知期中期末均分不到70的情况下,左老师给出了235的给分公式,甚至还要亲自批阅试卷,把一些地方的分扣掉(主要是第五题Fourier级数收敛性的证明)。能感受到助教老师给同学们放的洪水,但是两位助教老师也只能相视一笑,好像已经知道还有大手会把同学们挨个肘一遍。哪位同学在哪道题上因为什么扣了几分在纸上写得清清楚楚,然后公布在课程群里面。简单算一下,按照这个给比例,班上的总评均分不到75。相比之下,隔壁lsm班还向上调分。简直就是血流成河……
26.01.23出分再评:果然是一分不调……那么结果也很明显了,zdf班均G只给到了2.3左右,优秀率肯定没给满,中低分段是血流成河……这样的结果是不是早就有预兆呢,感觉左老师对学生的意见很大……