2021春 课程号:00125001
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
| 选课类别:计划内与自由选修 | 教学类型:理论课 |
| 课程类别:本科计划内课程 | 开课单位:数学科学学院 |
| 课程层次:专业基础 | 学分:4.0 |
教材:Elias M. Stein, Rami Shakarchi: Real Analysis
参考书:周民强《实变函数》,第三版
课程内容:教材第1~3章(不含打*号内容),第6章部分;依测度收敛和部分定理的证明参考周民强上相应内容
教学水平与课程内容
王兵老师的《实分析》课程主要按照Stein的内容授课,讲解测度、积分、微分等基础内容,个别定理采用了周民强的方法。尽管老师上课主要使用英文板书,并且脱稿讲解,能够将宏观思想讲得很清楚,但在证明某些定理时细节处理会导致节奏变慢,影响课程流畅性。助教的评价也支持这种观点,其指出王老师大部分证明讲得细致,但可能会卡在细节上。Stein上的题目被推荐作为课后练习,尽管作业量相对较少,每周仅四到五道题。
作业与教材推荐
王兵老师选择了Stein的教材作为主要参考,对于学习建议,助教则推荐Folland的《实分析》作为更高质的阅读材料。助教还指出,理解集合论及其在测度论中应用十分重要,可以边学边补充集合论。
考试与成绩
考试分为期中和期末两部分,分别占总成绩的30%和60%。期中考试内容较简单,但及格率不到30%,期末考试有助教参与命题,难度稍降。从成绩分布来看,总体给分较好,优秀率29.4%,多个学生反映给分“超好”,甚至有同学期末成绩较低(28分)也能获得2.3的绩点。助教提到,因原定比例下没有一人能上85,因此进行了调分处理。
评价与总结
整体上,学生对王兵老师的评价较好,认可其讲课水平高、思路清晰。尽管板书初期较乱,但在逐步适应后可接受。在教学互动方面,王兵老师强调理解定理比掌握证明更重要,建议学生多做练习。尽管课堂节奏偶有停滞,但整体课程内容扎实,为后续高级分析课程打下基础。因此,该课程还是非常推荐的,特别适合那些需要扎实基础的同学。据调查,王兵老师对低分段学生也非常友好,是除了赵立丰外的数院第一“大奶”。
课程总结
- 教学内容:讲解细致、思路清晰,重点内容包括测度论、积分论及其广义应用等。课程涉及面广,推动学生深入理解函数空间。
- 作业与课外阅读:作业量少,主要从Stein题目中选取,推荐辅以阅读Folland的《实分析》。
- 考试与给分:期中期末考试难度适中,总体给分宽松,但改卷严格,最后进行调分以反映学生整体水平。
- 整体评价:适合需要夯实基础的学生,教学互动好,对低分段学生友好,总体上是值得推荐的重要课程。
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:很多
我是这门课的助教。我于大一下学期学习了实分析(H)的内容(任课老师是任广斌),大二上学期旁听了科大高等实分析的课程(任课老师是赵立丰),并在大三下学期担任了这门课的助教(主讲老师是王兵老师)。作为这门课的助教,我仅以自己的学习经验,给选这门课的学弟学妹们写一些学习建议,希望能给大家提供或多或少的帮助。
写在前言:
实分析是近代分析学的起点,在分析学大厦中起着“地基”的作用。我们学习任何一门数学课,都要明确两个问题,一是这门课所要研究的数学对象,二是为了研究这个数学对象我们引进了哪些数学工具。在数学分析中我们的研究对象是一个单独的函数,所使用的数学工具是微分、积分、极限理论。实分析提出了一个全新的观点:我们不再单独研究一个函数,而是把一些函数打包成一个集合,组成“函数空间”这样一个整体。我们的研究对象就是各种“函数空间”,所使用的工具是“测度论”与“积分论”。分析学大厦中的一个重要支柱是利用“函数空间”去解“偏微分方程”,实分析将教会我们两个研究“函数空间”的重要数学工具。所以说,实分析是分析学大厦的一个重要地基。
教材与参考资料:
Rudin的“实分析与复分析”建议作为参考书,这本书内容很全,但在没有老师讲解的情况下,不太建议当作教材直接阅读(我个人认为不适合用于自学)。Folland写的“实分析”是我所有读过的实分析书中质量最高,写的最好的,也很适合自学,强烈推荐大家认真阅读。但这本书书写的难度对初学者较大,如果大家直接读Folland感觉很困难,可以先看看Stein或周民强的实分析教材找找感觉。王兵老师本学期使用教材为Stein,相关内容我已经发布在课程群。不过以我个人的经验,我还是要建议大家认真阅读一下Folland这本书。
考核方式:平时成绩(10%)+期中考试(30%)+期末考试(60%)
总评:由于期中期末的卷面分都不太好,按照原定的比例没有一人能上85,所以在上述考核方式的基础上又进行了调分,最高分95(给了三个),优秀率给到了29.4%,后面能捞的基本也都捞到60,总体来说给分还是相当不错了。
实分析这门课的核心内容是:
(1)测度论。
(2)积分论。
(3)利用测度与积分去研究函数空间(主要研究Lp空间与L2空间)。
(4)傅立叶分析与广义函数。
集合论的引入:
一些教材会在最开始花笔墨讲解集合论的东西,引入集合论的原因是我们在这门课的学习中会遇到不可数的集合,进行不可数次的运算,为了避免逻辑上的自相矛盾,我们需要引入选择公里。事实上如果你承认一些基本事实,那么即使不学这部分的内容也无伤大雅。但是对于一些有精神洁癖的同学,凡事都想刨根问底,那么跳过这部分直接学测度论可能就会有一些难受(比如用一些给定的集族生成一个sigma代数,它的良定性就需要集合论的相关知识)。我个人建议先开始进入测度论的学习,需要用到集合论的知识时再边用边学。知道后面需要用哪些集合论,然后再回过头补充。毕竟集合论绝不是实分析这门课的重点,如果一上来就纠结在数理逻辑的地方,容易死绕进去。
分析是极限的艺术,我们在数学分析中学过数列的极限,在这里我们要学习集合列的极限(类似地,当极限不存在时我们要定义上极限与下极限)。这样我们在后面学习“测度到积分的提升”时,就可以很自然的打通可测集与特征函数之间的一一对应。也正因为有了这个观点,我们便可以非常清晰的看到:集合是特殊的函数,测度是特殊的积分。
测度论:
测度,顾名思义,就是指如何测量一个集合的“度”,这个“度”是“长度”、“面积”、“体积”等概念的推广。Stein和周民强是从欧式空间的Lebesgue测度讲起,它是欧式空间上最自然最canonical的测度,是最符合我们直觉的测度。它的构造测度的步骤是:“(长方体的)体积->(任意集合的)外测度/内测度->(Lebesgue可测集的)Lebesgue测度”。Folland则是着重讲解抽象测度,在最一般的集合上建立测度理论,把Lebesgue测度作为一个具体例子。具体步骤为:“(长方体的)体积->(可构造集的)准测度->(Borel可测集的)Borel测度->(Lebesgue可测集的)Lebesgue测度”。这两种方法都是需要熟练掌握的,前者可以推广到几何测度论,后者可以推广到抽象测度论,而在欧氏空间上,Caratheodory定理告诉我们这两种方法构造出来的测度是等价的。我个人更加倾向于Folland的讲法,因为实分析就是要学习最一般的测度,为后续课程打下基础。例如我们在数学分析中学过的Jordan测度,在概率论中学过的概率测度。在以后的学习中,微分流形中会学到李群的Haar测度,几何测度论中会学到Hausdoff测度,黎曼几何中会学到黎曼体积测度,辛几何中会学到Liouville测度,量子混沌中会学到半经典缺失测度,等等。这些都是抽象测度论的具体例子。
在对一个具体的空间定义好了什么是测度后,我们很自然地要考虑更加整体的性质,即把所有带有测度结构的空间放到一起研究。注意到可测函数的复合依然是可测函数,这是一个范畴性质!所以所有带有测度结构的空间放到一起就不单单是一个真类,更是一个范畴!我们会在课堂上听到老师经常讲这样一句话:很多年后你们会忘记实分析这门课具体内容,但你们应该会记得Littleword三原理。这是一种哲学上的观点:可测集差不多是开集,可测函数差不多是连续函数,依测度收敛差不多是一致收敛。如果我们用范畴论的观点去看,Littleword三原理其实就是在比较拓扑范畴与测度范畴的关系。作为范畴中的对象,拓扑结构由开集刻画,测度结构由可测集刻画,Littleword第一原理(也就是Caratheodory定理)描述了这两个结构的关系。作为范畴中的态射,拓扑范畴的态射是连续函数,测度范畴的态射是可测函数,Littleword第二原理(也就是Lusin定理)描述了这两个态射的关系。这两个范畴中又都有极限结构,Littleword第三原理(也就是Egorov定理)描述了这两种收敛的关系。
从测度论到积分论的提升:
对比较特殊的欧式空间,我们会学习Lebesgue积分,它是数学分析中黎曼积分的推广。这里大家要理解:数学分析中学的黎曼积分有哪些不足,Lebesgue积分如何弥补了这些不足;黎曼积分中的许多定理如何推广到Lebesgue积分上去。但还是那句话,实分析不要只盯着欧式空间,要学习最一般集合上的积分,才能为后续课程打下基础。在微分流形中会用“形式张量”定义积分,在几何量子化中会对“半密度函数空间”定义积分,在广义函数理论中会利用“积分核”去定义广义算子,等等。
对于最一般的空间,如何从测度定义积分,是实分析积分论要掌握的核心知识。正如前文集合论中所讲,集合一一对应于特征函数,所以我们可以定义特征函数的积分,再由sigma可加性,我们可以定义简单函数的积分,再利用Levi单调收敛定理,我们进而可以定义非负可测函数的积分,最后利用绝对值可积,我们定义一般可测函数的积分。值得注意的是,这一系列提升的过程是非常标准的,它不仅做到了“把测度的定义提升到积分的定义”,这个提升还将测度结构下很多良好的性质与定理保持到了积分中。例如:测度论中的Fatou引理可以提升到积分论中的Fatou引理;测度论中的控制收敛定理可以提升到积分论中的Lebesgue控制收敛定理;测度论中的Fubini定理可以提升到积分论中的Fubini定理……更一般的,比方说一个测度空间满足定理A(这个定理A可以是刚刚提到Fatou引理、控制收敛定理、Fubini定理,也可以是其他的定理或只依赖于测度结构的性质),那么由这个测度结构所定义的积分也必然满足定理A。证明是标准化的,就是走一遍“从测度到积分的提升”,先证明特征函数满足定理A,然后证明简单函数满足定理A,再证明非负可测函数满足定理A,最后证明一般的可测函数满足定理A。
从积分的观点看测度:
在学完积分论后,我们以一种事后诸葛亮的方式回头再看测度论:测度论本质就是三条公理,而积分也满足那三条公理。唯一不同的是测度只能为正,而积分可正可负。我们只要将测度的定义拓展到可以取负值,那么测度与积分便统一起来了,Hahn分解定理告诉我们这样的拓展是可以做到的。在这种意义下,积分与测度就是一回事了。就像“鸡”和“蛋”的关系一样,积分可以看成测度(Lebesgue定理),测度也可以定义积分(单调收敛定理),二者相辅相成。从整体的观点看,我们可以把所有的测度结构放到一起(也是所有的积分结构),这便组成一个线性空间。在这个线性空间中任意取出两个不同的测度(记为u、v),由于测度与积分是一回事,我们不妨将u看成测度,将v看成积分,那么一个自然的问题便是:v这个积分是否是由u这个测度提升得到的?Radon-Nikodym分解回答了这个问题,它给出了v的一个直和分解,能由u提升得到的部分(即完全取决于u的部分),和与u相互奇异的部分(也就是与u完全无关的部分)。
注记2:关于泛函分析内容的补充
在函数空间的学习中,我们需要少许泛函分析的知识。正如前言中所说,实分析教会了我们两个研究“函数空间”的工具,泛函分析也是如此。泛函分析的研究对象是“赋范线性空间”与“线性算子”,研究工具是“拓扑”与“算子谱理论”,也就是说,泛函分析提供了另一种研究函数空间的工具。关于这部分,我个人建议,即使本学期没有泛函分析这门课,也希望大家通过业余时间自学一点泛函分析的内容(知道什么是Banach空间、什么是Hilbert空间)。
Lebesgue积分与Riemann积分的比较:
我们在前文提到欧氏空间中的Lebesgue积分是黎曼积分的推广,黎曼可积函数一定Lebesgue可积,L^1[a,b]是R[a,b]的完备化。那么我们很自然地会问,黎曼积分中的一些定理和性质是不是在Lebesgue积分的框架下依然成立呢?我们在数学分析中学过以下四个理论:牛顿莱布尼兹定理、局部积分公式、中值定理、链式法则。在推广到Lebesgue积分论的过程中,最重要的一定要知道,我们是在什么框架下推广的!!!在黎曼积分中,这四套理论都是在C^1[a,b]框架下建立的。在实分析中,局部积分公式可以建立在有界变差函数BV[a,b]的框架中,中值定理可以建立在绝对连续函数AC[a,b]或Lip[a,b]框架中,链式法则可以建立Lip[a,b]框架中,牛顿莱布尼兹定理可以建立在AC[a,b]/R~L^1[a,b]/a.e.,或Lip[a,b]/R~L^\infity[a,b]/a.e.框架下。如果框架选择错误,就会出现反例,例如有界变差函数BV[a,b]的框架中是没有链式法则的,也没牛顿莱布尼兹定理!
关于具体的计算:
这门课的计算题大致有三类:计算Lebesgue积分、计算有界变差、计算抽象测度。计算Lebesgue积分的常见方法有换元法、局部积分公式、中值定理、单调收敛定理、Lebesgue控制收敛定理。计算有界变差的常见方法有导函数的黎曼积分、计数函数的积分。计算抽象测度的积分,要么是直接使用定义,要么利用分布函数转化为黎曼积分。每种计算的每种方法都可以在书上找到课后习题,这部分的内容就是靠做题练的,没有捷径。
函数空间及其上面的拓扑:
在分析学的大厦中,我们会遇到各种各样的函数空间,这门课我们主要学习两种最为基础的函数空间:Lp空间,它是一个Banach空间;L2空间,它是一个Hilbert空间。Lp空间的对偶,以及各种积分不等式的估计,是这一部分的学习重点。到了这个阶段,大家必须明白:“理解定理”比掌握“定理的证明”更重要。大家必须自己体会为什么这个定理有资格叫作定理,它为什么重要,有哪些应用?“掌握定理本身”比“会做题”更重要,这与我们之前学习的数学分析、线性代数等课,在学习模式上有着本质不同。举个例子:在积分不等式的学习中,我们会遇到一个重要的定理,Riesz-Thorin插值不等式。它的证明用到了调和分析的技巧,在这门课中是不做要求的,而且在后续的学习中,也基本没有地方会用到它的证明。大家初学的时候,可以直接跳过证明,但必须要理解它为什么重要(它刻画了当p在一个区间上连续变化时,一个线性算子在这一系列不同的Lp空间上,有着怎样的联系)以及它有什么应用(在傅立叶变换与广义算子的有界性控制中,起着重要作用)。
研究函数空间的各种拓扑结构之间的关系,事实上就是各种收敛性之间的互推。我们这门课常见的收敛大致有:几乎一致收敛、依测度收敛、几乎处处收敛、依L^1范数收敛、控制收敛……它们之间的关系大致为:
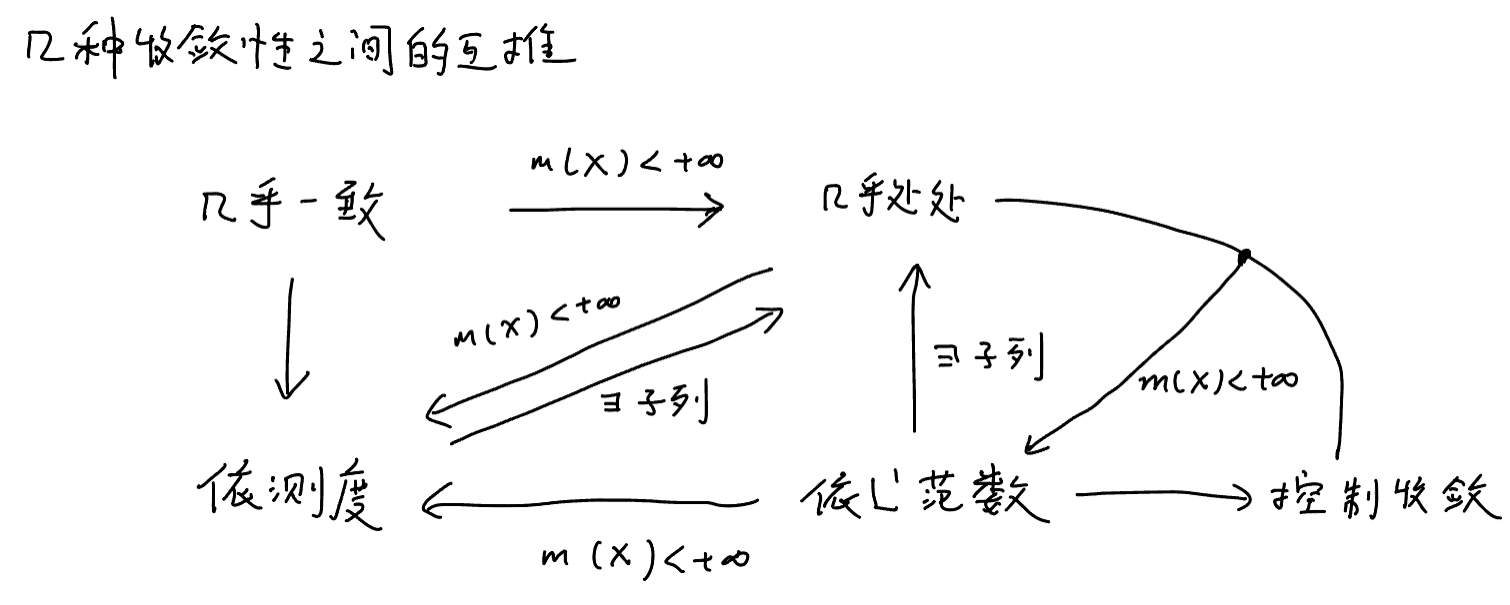
而对于那些没有包含关系的收敛,我们要能举出反例,常见的范例大致有以下几种(应该可以应对90%举反例的题目):
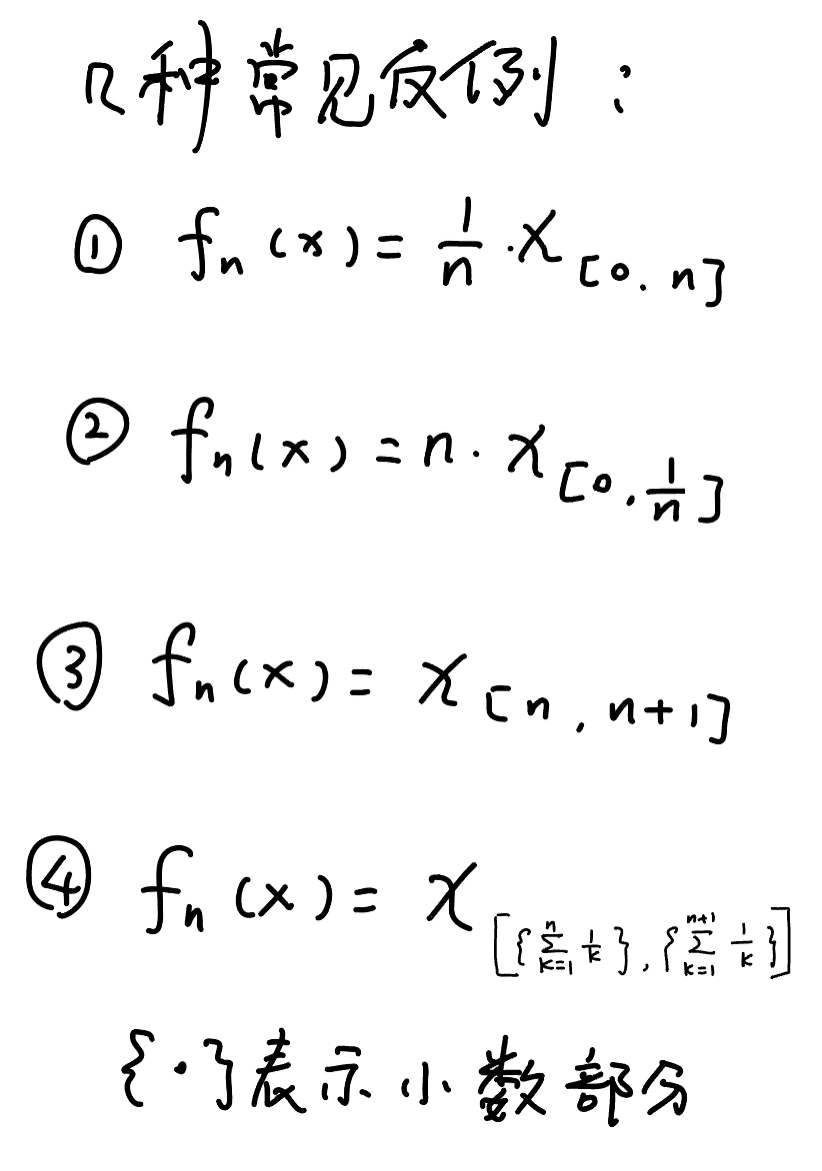
傅立叶分析与广义函数:
这一部分并不是实分析的标准内容,只是作为实分析的拓展和应用。为我们后续学习更深入的分析课程打基础。这部分的内容包括卷积,带有参数的傅立叶变换,以及在此变换下,函数的Lp范数是如何控制的(这就涉及到一些不等式),以及傅立叶变换有哪些应用(将求导转化为乘法),等等。广义函数也叫“分布理论”,它是一个非常重要的函数空间。当我们把微分算子看成从一个函数空间到另一个函数空间的映射时,我们很自然地会问,这个映射的定义域是什么?紧支撑的光滑函数是很好的函数空间,几乎所有的微分算子都可以作用上去,它包含在这个映射的定义域中。但我们要真正搞清楚这个映射的定义域,就必须扩大我们已知的函数空间。事实上,我们所能涉及到的最大的函数空间就是广义函数空间。例如傅立叶变换的定义域是“缓增分布空间”,半经典拟微分算子的定义域是广义Sobolev空间,等等。这些函数空间都是广义函数空间的子集。学习广义函数,我们所能处理的函数空间就更大了,这也就方便我们进行各种操作。
傅立叶变换其实本质上是一种泛函演算,是对求导算子进行的演算,将微分算子与多项式一一对应起来。算子是复杂的,而多项式是简单的。进一步观察我们可以发现,傅立叶变换将k次求导转化为了x^k,而作为函数我们不需要要求k是整数,所以我们可以对一般的实数k(例如k=1.5),利用傅立叶逆变换,便可得到“求1.5次导数”这种操作,这种对导数的推广就是拟微分算子。学过微分流形的同学,可以进一步学习流形上的广义函数,利用单位分拆的技巧,傅立叶变换可以自然地推广到流形上。
- 课程难度:困难
- 作业多少:很少
- 给分好坏:一般
- 收获大小:一般
- 难度:困难
- 作业:很少
- 给分:一般
- 收获:一般
课程内容
没太多好说的,王老师基本完全按照Stein上的内容讲的,就是测度、积分、微分,再加一丁点抽象测度,个别定理的证明采用了周民强上的方法,补充了依测度收敛(这应该都算不上补充),没有讲Lp空间。可能是中间有几次课节奏太慢了导致最后抽象测度讲的内容实在太少,最后考试也没涉及。
王老师上课全英文板书,大部分时间是脱稿的,会把一些宏观的思想讲得很清楚,但在证明一些定理时可能会在一些细节的验证上卡住,导致上课的节奏被拖慢,课程的流畅性降低。大部分证明讲得比较细致,有些重复使用的技术用到时也会再写出来,王老师对此的解释是“如果你觉得我写的这些都是废话,那就说明这块内容你掌握了”。课程作业非常少,每周就四五道题,但王老师在课上曾指出如果你想学好这门课,那就把Stein上的题全做了。个人认为王老师这学期讲得最好的一节课就是讲度量和测度的关系,引申到曲面上的度量,然后介绍Gauss绝妙定理的那节课(就是有人来拍照录像的那次)
关于考试
期中考试考前两章(测度和积分),王老师觉得卷子出得挺简单,结果卷面成绩及格的不到30人(这个班总共121人)。期末考试考讲过的所有内容(本来说有一道抽象测度的题选做但最后也没考),有一位助教参与了出题,试卷难度整体降低了,具体成绩分布未知,但从均分来看并未改善太多。从题目本身来说并未涉及偏题、怪题以及技巧性太强的题。
关于给分
从我自己的成绩来看给分应该算挺好的了,优秀率29.4%(算法是优秀率上限×出勤率),但王老师好像只给了三个95以及好多个94,助教对此的解释是“4.3是一个非常严肃的事情,必须非常非常优秀才能拿到”。
总的来说这学期王老师的课没能达到我的期望值,只能算是中规中矩,但毕竟这是王老师第一次带本科生课,要求也不能太高。
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:一般
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:一般
wb对低分段很友好,除了zlf外的数院第一奶王!无脑选wb!期末28 还能有2.3!
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:很多
总体上还是很推荐的。
老师的水平非常高,讲课思路很清晰,虽然板书一开始有点乱看不懂,后面慢慢适应了也还可以。实分析之前零零碎碎学过一些,但跟着老师学过一遍之后才知道自己学的有多拉跨。。。
作业大概是大二下几门课里最少的了吧,每周最多4道题,全都出自Stein习题。
期中期末难但也没有特别难,虽然改卷好严,但是最后的总评却是出乎意料的高。
- 课程难度:简单
- 作业多少:很少
- 给分好坏:超好
- 收获大小:一般
- 难度:简单
- 作业:很少
- 给分:超好
- 收获:一般
老师很奶,优秀率给了30%出头,老师讲课比较慢,比较细致,但偶尔的时候会挂黑板哈哈哈,比较适合慢慢学的同学