2026春 2025春 2024春 2023春 2022春 2021春 2020春 2019春 2018春 2017春 2015春 2014春 2013春 2012春 课程号:00170201
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:一般
| 选课类别:计划内与自由选修 | 教学类型:理论课 |
| 课程类别:本科计划内课程 | 开课单位:数学科学学院 |
| 课程层次:专业核心 | 学分:4.0 |
教材:周民强《实变函数论》
PPT主要参考Folland
教学质量与课堂风格
任广斌老师的《实分析(H)》课程因其独特的教学风格而广受讨论。任老师采用PPT授课,有学生反映PPT过于简略,但也有认为老师在课堂上以深入浅出的方式讲解数学概念、构建知识框架,强调思想性。这中间的差异可能在于学生个人对PPT的接受程度及对于"高观点低难度"这一讲课方式的适应度。
课堂内容
课程大纲涵盖了集合论、Lebesgue测度论、Lebesgue积分论、抽象测度、微积分基本定理和(L^p)空间等。部分学生认为课程内容较少且深度不够,尤其是一些高级或拓展内容未作详细讲解。不过,对于实分析核心内容的讲授,任老师通过比喻等手段使复杂概念更为直观易懂,使学生能够较好地掌握课程主线。
教学方式
任老师的课堂中规中矩,讲授内容循序渐进,不急不躁。不过,使用PPT教学使得课程失去了一部分数学课的传统板书感,这对部分学生的适应产生影响。任老师曾尝试转换为板书教学,显示出对教学反馈的重视和开放性。
作业与考试
作业以周民强的题目为主,被部分学生认为简单,缺乏挑战性。考试有被描述为“PPT背诵大赛”的趋势,主要考核PPT中出现的内容。在设计上显得轻松,尤其是理解PPT内容者很可能在考试中获得良好成绩。
给分与学术反馈
课程给分普遍较高,是选择这门课的一个主要因素。虽然学生水平与背景有差异,但即便期中或期末成绩不理想,最终仍可能获得不错的总评。助教出卷并在给分上相当慷慨,也对学生体验有积极影响。
课程改进建议
尽管任老师对教学质量与学生反馈持开放态度,未来课程可进一步调整教学内容,增加挑战性,并确保教学资源(如PPT、教材)的充实。这门课适合那些希望通过轻松的考试和良好的课程大纲掌握实分析基础的学生,但若想深入学习仍需综合利用Stein或Folland等其他教材资源。
总评
任老师的《实分析(H)》课程以轻松的教学氛围与良好的给分著称,但在课程内容深度与覆盖面上,尚有提升空间。适合自学能力较强,习惯自我补充知识体系的学生。
- 课程难度:中等
- 作业多少:中等
- 给分好坏:一般
- 收获大小:没有
- 难度:中等
- 作业:中等
- 给分:一般
- 收获:没有
25 秋补评:看到这学期有23级学生反馈任✌🏻数学分析A1用板书不用ppt讲课进度过慢,感觉任✌🏻可能要无语了🤣
各位旅行者大家好,我刚刚从稻妻跑完委托回来,现在可以集中时间来回应大家关心的问题。针对最近大家在版本讨论中出现的一些误解,我想在这里做一个比较系统的说明,希望大家能够认真阅读,并从中获得清晰的理解。
⸻
一、关于“是否有保底机制”的误会
这部分的误会已经由(深渊代打大神)帮助大家发现并澄清了,值得大家学习。
讨论的焦点是是否存在保底机制,而不是“保底是否容易出货”。从事实来看,确实存在保底机制,因此当事旅行者的说法并不成立。如果该旅行者本意是说概率太低、容易歪,那他在表达上确实存在“词不达意”的问题。这个误解的责任,应该由表达不清的一方承担。
在此特别感谢的细致入微的观察和指正。他不仅是大家的队友,更是老玩家中的“璃月七星”,非常值得大家尊敬与学习。
⸻
二、关于旅行者的意见
旅行者提出了质疑,但显然并没有真正理解米哈游的原意,产生了强烈情绪反应。这种误会并非源于官方机制,而更多是因为对信息的误读。
首先,关于“偷换命题”的问题,第一条已经说明得很清楚了,这一点与策划无关。
更关键的是,米哈游多次强调:不能单靠B站剪辑来了解版本内容。正确的探索方式是“直播为主,攻略为辅”。如果没有完整看直播,只看短视频,容易误解内容、甚至抽歪一池子的原石。我已经多次强调“看直播、看直播、看直播”,但显然没有得到足够重视,为此我安排了小测验和数据复盘。
旅行者说自己关注了更新,也参加了版本测试,的确如此,我对旅行者记忆颇为深刻。他具有好奇心强、勇于发问的优良品德,这在社区中非常难得,值得表扬。我欢迎任何旅行者“不懂就问”。但遗憾的是,旅行者缺席版本前瞻次数较多。
请记住一句话:批评机制之前,先问问自己有没有听从策划的语重心长的建议:看直播。
⸻
三、关于攻略和材料的公开与使用
有些旅行者对攻略材料提出了看法,我想统一回应:
一般来说,米哈游并没有义务公开全部数据。因为一旦被搬运,容易被商业号二创变现。
但我出于帮助旅行者探索提瓦特的初心,还是选择公开我的路线图与组队建议。这本身就是对大家掌握机制、精通打法的期望。
如果你完整参与了活动,仍然对配队或抽卡存在困难,我们还有两位策划助理提供答疑支持。我自己在每次更新后也主动开直播复盘,耐心讲解,目的是让大家真正掌握机制。
看直播 + 攻略笔记 + 助理答疑 + 官方答疑,这是提供给大家的标准通关路线图。如果省略其他只保留剪辑一个选项,这相当于选择了还没开放的野图路线,应该自我负责,而不是指责版本,要求策划开荒未开发区域。我在提瓦特已经探索了37个版本,这份热情和责任感是一直未变的。希望大家能够珍惜。
⸻
四、再次强调探索方式
请大家一定要重视游戏内容本身,认真观看前瞻。攻略只是辅助材料,如果不参与游戏内容,对机制的任何负面评价,都是对自己不负责任的表现。
⸻
五、欢迎参与优化攻略
如果大家确实愿意在野路子中整出新活法,有意愿成立兴趣小组,对攻略内容进行改进,我非常支持。我可以提供原始的 TeX 文件供大家编辑。可以负责这件事。
说实话,众口难调。比如有旅行者提到“逐行展示机制”的形式,实际上意见不一,有人认为这是遮遮掩掩、不利于复盘。提醒大家,攻略不是神之眼,每个人对“好攻略”的定义不同,人见人智。如果意见分歧太大,不再公开原始攻略材料也是一个可能的选项。
⸻
最后寄语
希望大家在提瓦特的旅程中真正打下坚实的机制基础,不仅仅为了出金,而是为了真正享受游戏。我们愿意全力支持你们,但前提是——你们愿意认真探索。
让我们一起把这款游戏玩明白,不辜负彼此的原石与热爱。
——致每一位认真探索的旅行者 敬上
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:很多
"我们走后,他们会给你们的成绩审核通过,会提高你们的优秀率,这不是因为他们良心发现,也不是因为他们变成了好人,而是因为我们来过。"
今天上了一节课后,大一上熟悉的感觉回来了。可以说很久没听过如此酣畅的数学课了
上任爷的课,恰似乘观光巴士游览景区。
这辆车速度不快,没有心惊胆战的狂飙;这辆车不会停车,没有始料未及的急刹。
到达每一处景观时,乘客无须急忙掏出手机拍照,担心下一秒就错过精彩,而失去了端详品味的兴致。
路过崖侧的青松,一瞥便能尽收旖旎于眼底;行至无垠的花海,这辆车会带你遍历一切路径,从不同视角欣赏其全貌,直至完全内化于心。
这趟旅程景致缤纷,上车时的兴奋、路途中的惊叹、下车后的满足,皆不虚此行。
什么是任爷?
他说:
人类是宇宙的眼睛,数学是人类的眼睛。
他说:
实分析是积分定义最广的场所。
他说:
数学是一门仿生学。
他说:
八元数统一人类社会。
他说:
集合X,我们视为宇宙。
他说:
Zorn引理是一步登天的膨胀法,具体表现为稳扎稳打、得寸进尺、一步登天。
他说:
它们两个打乒乓球,不断地拉回。
他说:
当时美国用的是c,苏联用的是\(\aleph\),其他国家呢?其他国家说了不算。
他说:
Cantor集上的居民,生活在分数维空间。
他说:
Cantor函数几乎处处不学习,但最后能拿满分。
他说:
可测集能将任意集合很好地一剖为二。
他说:
没有一把万能的尺子。
他说:
要避开\(\infty-\infty\)的陷阱。
他说:
可测集可以由开集收缩的到,或者由紧集膨胀得到。
他说:
外测度的下半连续性是Fatou引理的另一面目。
他说:
开集中的点是有房一族。
他说:
令人无法接受的是,\(\mathbb{R}\)中不可测集的势竟然也是\(2^c\)。
他说:
可测集差不多是开集。
他说:
可测函数差不多是连续函数。
他说:
几乎处处收敛差不多是一致收敛。
他说:
可测函数的分解,就是原子搭积木。
他说:
和可测函数的四部曲一样,积分的定义也分四步走。
他说:
处理双指标的时候,用到min阀门技巧。
他说:
测度是对特征函数的积分,而积分是一种测度,称作“绝对连续测度”。
他说:
实分析中没有级数理论,因为级数就是一种积分,是关于计数测度的积分。
他说:
Riemman是采用切片面包的方式,而Lebesgue采用的是分层蛋糕的表示。
他说:
这个Fatou引理就像我们科大的学生,在校内看不出什么,拿到社会上就变得很厉害。
他说:
控制函数可以防止面积逃逸到无穷。
他说:
好久没写字了,胳膊有点累。
他说:
取不到极限是因为框架太小了,我们要把框架搭大一些。
他说:
实分析的顶峰,就是交换次序的等价定理。
他说:
测度论的顶峰是Radon-Nikodym定理。
他说:
昨晚喝了一杯咖啡,一晚上没睡着,如果我站着睡着了,请把我叫醒。
他说:
量子物理研究的是Hilbert空间中非有界自伴算子的谱。
他说:
Fubini一统天下。
他说:
把它分成“好+小”两部分。
他说:
Vitali覆盖是分析的手术刀。
他说:
\(L^p\)空间是边角料中的边角料。
他说:
对偶和变分是分析中的两大法宝。
他说:
测度论和积分论是实分析的双子塔,美国的双子塔已经倒了,但我们实分析的双子塔不会倒。
他说:
一学期下来,我们也到了收获的季节。
他说:
分析是极限的艺术。
- 课程难度:中等
- 作业多少:很少
- 给分好坏:一般
- 收获大小:没有
- 难度:中等
- 作业:很少
- 给分:一般
- 收获:没有
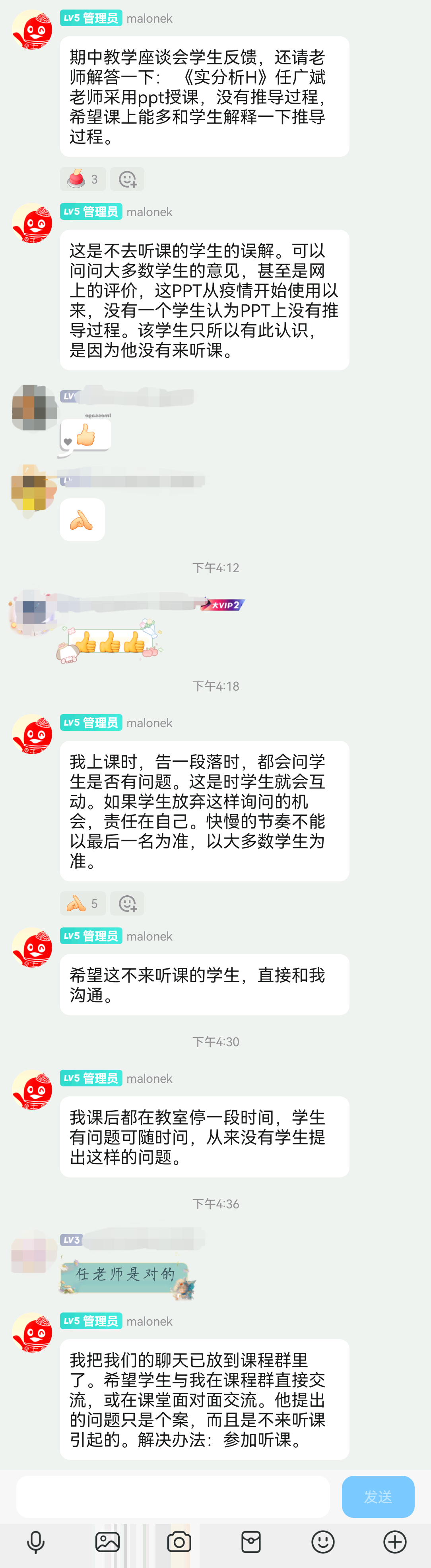
在此之前,任广斌给我的印象是一个PPT挺烂,讲课还行,比较和蔼的教授。但经4月18日此言一出,他在我眼中便彻底成为了一个犯了傲慢之罪的教授。
当学生向他提出问题时,他的反应不是思考自己的PPT是否有不合理之处也就算了,居然开始在没有任何依据的情况下指责提出建议的同学不来听课?
即使抛开PPT究竟有没有问题不谈,这样面对问题的态度也很恼人。何况任爷的PPT也是众所周知的可读性差。
为什么当他停下来时,没有人提问?
因为晕的人压根不知道从何问起了。
为什么任爷的课没有人来?
不是因为不来才听不懂,而是因为听不懂了才干脆不来。
我希望任爷在听到别人给他提意见时,至少先思考一下自己教得是不是的确有些问题,而不是只知道反过来指责提出建议的同学。
希望吧。
二编:任爷回应了。
其实我之前还是觉得任爷应该是会改进的。
以下是在群里有人指出问题后,任爷在群里回应的原文:

……有效信息是多少大家自己判断就好,我不替大家做主观判断了。
唉唉。

那么在他批评学生不来上课之前,又有没有问过自己是否把课上好了呢?
三编
任爷似乎红温了。
周一早上一来直接开始全覆盖点名,还数人头防止大家代签。
于是在各位同学的呼朋引伴下教室变成了这样

该怎么说呢,能让入座情况和政治课有得一拼,任爷也是有点水准了。
另:任爷开始板书了,这算一个进步,不过依然无法挽回之前的恶劣态度。暂时保持1分不变。
其实任爷的课上得并不糟糕,只是糟糕的PPT确实拖累了水平。在大家向他提出建议后,他却以同学不到课为借口转移话题,对现实存在的问题避而不谈。唉,任爷也是玻璃心了。
四编
周三任爷的复习课全在用板书,这是一个进步,如果任爷只是嘴上说说傲娇的话,实际上有所改进的话,我将酌情将分数上调。
希望我不要擅自期待吧。
五编
周一上课,还真不用PPT了
不过鉴于其此前的态度,再观望一会儿
六编
任爷真的不用PPT了。
看来任爷还是能听进建议的,虽然同学们一开始只是建议任爷PPT写得详细一些。
接下来我再提一点吧。希望能有一套配套的教材或者讲义,因为任爷讲了很多周明强书上没有的。这些东西如果课上没搞懂,希望能有一本参考书可以参考。
相应地上调评分。
七编(怎么这么能编)
确定了,后续课程采用板书上课。
任爷是听劝的
- 课程难度:简单
- 作业多少:很少
- 给分好坏:一般
- 收获大小:一般
- 难度:简单
- 作业:很少
- 给分:一般
- 收获:一般
原本写了很多, 感觉也没啥必要, 不如写写任✌. 六旬老人, 重新开始板书, 认真授课, 值得每个人尊重. 有些深刻的思想, 初看或许就略去了, 复习时才恍然注意, 因此这门课还是让人有所收获. 即兴仿词一首, 歌以咏志.
临江仙
滚滚流年东逝水, 岁月愁了白头. 三十五载转头空, 五教依旧在, 几度夕阳红.
六旬老汉三尺上, 惯看人去楼空. 今朝一聚生皆从, 分析那点事, 都在极限中.
出分后有点好奇任✌的给分公式, 感觉参考了较多的期中成绩? 或许给分在普班选课人数大增后也没有那么夸张了. 还是觉得不要为了给分选H课吧hhh
- 课程难度:简单
- 作业多少:很少
- 给分好坏:超好
- 收获大小:一般
- 难度:简单
- 作业:很少
- 给分:超好
- 收获:一般
时来天地皆同力,运去英雄不自由。
实分析哦圆满结束。这个给分感觉应该是跟往年一样不错。考试也延续了默写PPT的传统。期中前有一次小测和一次点名,并且声称会有三次小测,但后半学期实际上并没有任何小测和点名。
教学内容方面,有人说讲的比普班少,真学东西还得是普班这类的言论,感觉并不客观。我在考前做了近三年的普班期末试卷,并没有超过任广斌讲课范围的东西。
但话又说回来,这门课的内容安排极不合理。前期浪费了太多时间在集合论上,最后几周几乎只讲了微分这一边角料内容,直到倒数第2个ppt才简单介绍了Lp空间,holder不等式,闵可夫斯基不等式这样的大本营内容(甚至还不用插值定理就证出了一般情形的杨不等式)。
总的来说,在任广斌退休之前,自学能力强的同学可以无脑选这门课,并且通过folland学习真正的实分析,考前两天背诵ppt即可。
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:很多
今年第二次带这门课助教,整体内容与去年大同小异。随着mj教授的改革,H课的给分也迎来新时代,今年一共选课51人(有一人是0分,相当于有效人数是50人),有25人总评拿到95以上(含95),36人总评拿到90以上(含90),成绩顺利审核通过。
附一下今年的考试题(助教出题):
在科大数院跟着任爷上过两门课:实分析H与数学分析A1,这学期担任任爷的助教,简单写几句。
关于课程:
实分析课程的内容与学习建议我已经在王兵老师的评课下面写的比较详细了,任爷除了实分析标准内容之外,还会讲一些集合论与点集拓扑的知识。但相比华班学生的知识接收速度,任爷讲的确实有些慢了。
关于考试:
任爷每年都会让助教提供一些考试备选题,最后基本上80-90分都是助教出的,所以从往年试卷推测当年的出题风格是不可能的。我提供的期中题如下: Please login to download the attachment。
关于改卷:
期中改卷标准非常严苛,不过也可喜地看到在如此严格的扣分下依然有学生能拿到96的高分。期末大放水,不少人拿到了卷面100,班级中位数87。
关于给分:
第一次上传的分数被打了回来(jwc嘛。。。懂得都懂。。。)好像是新规定了总评平均分不能超过85,反复试验了几次,最后调分后总评平均分84.9,一共39人,90以上给了17人,任爷已经尽力了。说真的,华班的优秀率其实应该再高一些。
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:很多
知道jwc没有马,也知道任爷是被jwc压力不得已而为之。
但是这一条逆天政策总不是jwc的直接指示吧…这可要比单纯的点名计入平时分严重多了。

upd:有理由请假的也要为难一下是吧

感觉wdh已经可以说是全科大最伟大的助教了
为方便同学们期末预习和23级卷批预习传个ppt合订本(应该跟23年没啥区别):
upd:
任爷考试不为难人这点还是很认可的,等到出分了再来重新评分
很多人都抱怨今年选课的人水平低地太夸张了,这里面包括很多学长,虽然事实上就是这样的(怎么感觉比普班还夸张)但是也听到一些学长说这件事情的时候举的例子是某最后一节课谈谈对实分析理解的高手,只能说很难评价
upd:
这个给分确实挽尊了,加上wdh和rgb的一波操作基本上把小测和签到事实上无效化了,但是就冲着最后这几周糟糕的体验我还是把这个1分留在这里
rgb的课今年评价突然变差很多,但对于以后的同学而言他的课还是有一选的价值,毕竟我还是认为不是所有人来这里都是为了学好知识的
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:没有
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:没有
首先声明一下,任爷是个非常朴实可爱的人,和他交流数学或者人生想必是件愉快的事,正因如此我才更为这门课感到遗憾,它缺乏荣誉课程的自我修养。对课程本身我最多打到六分,但出于充分的助教工作、宽松的要求、对良好给分的妥协,我打了七分。
周一连上三节,第一节能对着前几页毫无内容的ppt讲上45分钟👍,后两节开始赶ppt,往往到最后还要跳过些内容。
不是,你这一次课连一个ppt都放不完是不是有些说不过去了。。
ppt上细节大多需要自己补充,当成小练习也没什么不好的,懒妈妈才能生出勤快孩子。但是整个学期上下来,感觉就是做了一遍周民强习题四,学会了用Lebesgue控制收敛这种傻子都会用的定理而已,真的不如自己看书,任爷这套老油子上课话术应该也产生惯性了,很难指望以后有改进。
dh助教是知识水平和表达能力都非常优秀的助教,如果不是真的想分享知识帮到后辈,我想没有什么动力能支撑一个人写出这么多份十几二十页的讲义(微分方程和实分析均如此),奈何我对这门课实在不上心,之后如果机缘合适的话可能会看看。
考试的话,如果认真看过一遍ppt并背诵了典型方法,那么大部分题真的是秒,起码六七十分吧。最难的二十分不是很好拿,不过凑点过程也能拿到一个很可观的分数了。期末以附加题的名义延长了半小时,有充足时间思考所有题目,体验非常好。改卷我反正是被捞了。
你院一旦有门课给分超好,第二年就有超多人选,宁方程尚可理解,跟风来实分析H班上的起码五六十个吧,个个都觉得自己是前一半吗。。新编:我狭隘了,不需要考到前一半也可在查看总评后嘴角上扬。
如今为了准备一门动力系统的课恶补(本该在实分析课上讲授清楚的)一些抽象测度,感觉\(\href{https://perso.telecom-paristech.fr/decreuse/_downloads/c22155fef582344beb326c1f44f437d2/rudin.pdf}{\rm{Big\;Rudin}}\)的第二、六章可作为很好的资料,基本覆盖ppt对应内容且简洁明了。
目前来看实分析对于一些方向的学生还是十分重要的,这些学生如果修读这门课的话至少还要自学基本的测度空间知识、紧群与Harr测度。
- 课程难度:简单
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:简单
- 作业:很少
- 给分:超好
- 收获:很多
时来天地皆同力,运去英雄不自由。

彻夜睡不着觉,再多说几句吧。通过这门课我们也能深刻体会到一些函数性质的意义。比如Vitali定理刻画了L1和m的关系以及一致可积对于控制收敛条件的细致刻画,包括Littlewood三原理和一些测度正则性对差的函数和集合的处理方式。更细致的比如说AC等价于BV+C+Lusin N property这样的东西没有被提及。实分析重点在这些东西上能够给人以好的分析上的直觉。以及书写上确实要注意,像我就会经常跳关键步骤(虽然补上不难),不然这门课就会变成语文课。实分析本身是不需要深入挖掘的(类似点集拓扑),而是醉翁之意不在酒,在于其结论在其他方面的应用。(比如你再也不用担心积分与极限换序,比如你的各种展开的种种性质即使不那么好也没关系)
然而最后因为一个Lorentz吸引子般的场外因素期末寄了。平心而论这种非智力不可控因素确实不在意料之内,但是因为不是自己知识的原因考低分肯定是一件不公平的事情却也没办法。但毕竟分数乃身外之物,王鼎涵是一个非常好且有耐心的助教,任爷上课也很认真且有趣,我也学到了很多知识,为什么又彻夜睡不着觉呢。bc
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:一般
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:一般
难度中等-作业不多-给分超好-收获一般 大概是这门课比较合适的评价 任爷还是很好的 后来也发出了大部分的ppt 但过于简洁的证明思路书写还是会让人在理解上产生不少困难(内容含量(zmq1-6和一点点抽象测度论 但比较阴间的部分都不会涉及)与作业都不算多 因此可以摸 实分析也算是相对可以速成的科目 成体系地理解概念之后 任爷的考试一般不会涉及什么变态技巧)
期末放水 但我因为有个ppt上的定义没注意到喜提-8 这个故事告诉我们书和ppt都得好好看
- 课程难度:中等
- 作业多少:很少
- 给分好坏:一般
- 收获大小:一般
- 难度:中等
- 作业:很少
- 给分:一般
- 收获:一般
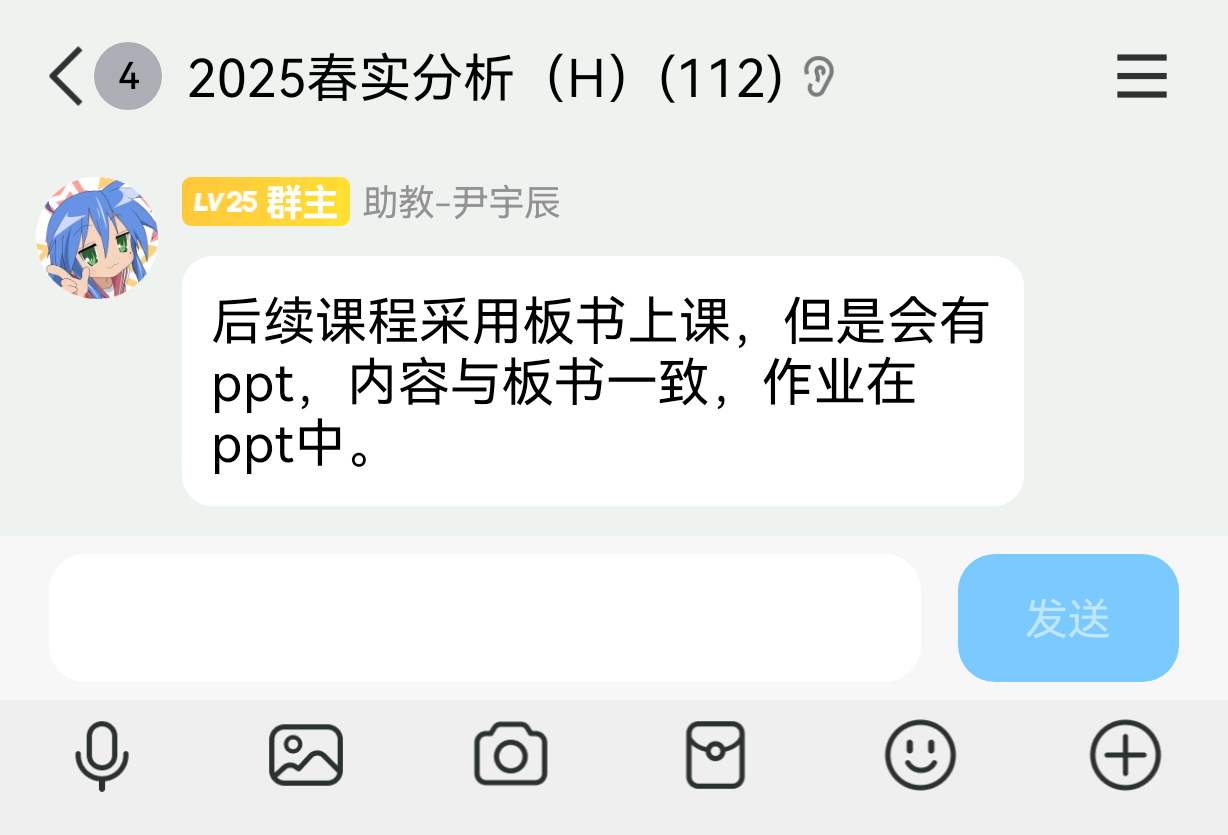
周一345前线报道,上周三刚小测这次又数人头点名,彻底发疯了
作为两次都到的既得利益者仍然对此丧心病狂的报复性举动感到无比心寒,任✌🏻的传奇已彻底落幕了。
2025.4.28前线报道
任爷似乎开始全面使用板书,暂时先观望一下🤓
- 课程难度:困难
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:很少
- 给分:超好
- 收获:很多
很抱歉拉低了大家的平均水平……
没错,我就是那种冲着pksq给分好+内容“比较适合入门学生”+看到课堂容量疯狂扩充到100人才来的同学……
我看好多同学都说任爷讲得慢、内容少等等;但我觉得内容已经好多好快了……任爷讲“废话”的时间刚刚好是我用来课堂消化的时间……
(也许应该把任爷带的实分析H变成普班课???然后把H课换成内容更丰富的,这样看上去可能会更符合花瓣高手的预期……阿巴阿巴……)(不过其实我也并不清楚普班比H班多上了些啥……)
然后就是,感觉考完以后,就我一个人觉得这次考得难……怎么说呢,很受打击;以及就是,还好没选普班课,不然指不定被怎么薄纱……
呃,关于小测和签到,任爷倒是在课后提过一嘴是怎么回事。
任爷说是因为这学期上头(我记得好像是教育部?)来人检查了(几年一轮的那种)。锅似乎还真不主要是jwc的。
【哦,我印象中,记得这群检查的人还会干一件事情,就是抽查批改的试卷和这份试卷的主人对应的总评成绩。要是抽查出来他们认为不合理的判卷(指判卷过于宽松)或者不合理的总评给分(指总评捞得过狠),老师就会受处分……】
以及dhgg是大爹!(细节不说多了……)
最后,纯好奇,最后一节课那位同学分享了些啥内容啊?
出分了。
任老师和dhgg是叠!
本来以为要亖了,结果居然给4了。这样看了估计优秀率起码得有70%了吧。
是真奶啊!
- 课程难度:简单
- 作业多少:中等
- 给分好坏:超好
- 收获大小:一般
- 难度:简单
- 作业:中等
- 给分:超好
- 收获:一般
这课对于妮可数批就等于终点之于舞萌痴,不吃这分的树皮有难了
期中比中位数低6分期末比中位数高10分总评90,rgb和wdh你是我爹
诶但是dx2025更新了终点降定数到13.7了,希望这门课的风评别降
- 课程难度:简单
- 作业多少:很少
- 给分好坏:超好
- 收获大小:没有
- 难度:简单
- 作业:很少
- 给分:超好
- 收获:没有
省流:水课
就这还指望H课绩点乘1.1呢?某学期大量人冲着上一年的好评来选结果没人到课搞得要多次签到,什么水分不用我说了吧\偷笑。
球球你院换个老师来教吧,任爷毕竟还是老了。反正也不指望在这门课上学到什么东西了。不建议想走基础数学方向的同学选这门课,或者你能确定脖子烤可以不烤分析那也无所谓。否则,还是在普班扎扎实实地学吧。即使你在华班不想学组合学进阶/概率论进阶/具体代数而不得不修这门课,也最好旁听普班/自学。我相信华班同学的自学能力是非常不错的,至少对于这门课来说,自学的效果会更好。
以下为原评论
任爷讲课很接地气,经常会用一些通俗的话语解释实分析里的基本思想,但是我认为只听这些东西的话还是会缺乏对数学本身应该具有的严密性的认识。用PPT讲课就更是如此,讲一些证明过程的时候就像是在念latex代码,听下来还不如我自己自学的时候认认真真的在纸上follow一遍收获大。这也是我为什么坚持认为数学课用板书讲课才行。至少对于实分析这门课,这么做非常有助于对初学者的“分析功底”的构建,而这是仅凭“把证明念出来”所无法做到的。
讲zmq的内容至少我可以课后自己重新学一遍,讲其他一些补充内容的时候,虽然我在看其他教材的时候自己就学过一遍,但是再听他讲的时候还是觉得云里雾里,甚至没有我第一遍学的时候那么明白。当然补充内容也不考,听不懂也就无所谓了。
作业都是zmq的习题,不是太水就是太多技巧。我在自己把Stein前三章的习题做了一遍之后就觉得做zmq上的题就是为了做题而做题,做过之后对理解整一个所学内容其实没有多大帮助。相比之下Stein的习题就很多干货,像普通班今年期末考就考了大量上面的原题,但是个人觉得能把这些题理解清楚,实分析这门课也就基本上算是学懂了。(不过zmq的正文内容还是不错的,一些比较重要/奇怪的例子的构造实际上也是Stein的习题)
给分的时候有点小插曲:
最开始助教帮任爷拟定了给4.3,4.0,3.7各十个(总人数39),但是据说由于教务处新增了“均分不能超过85”的规定,最终结果如田助教的评论里所写。由于此事事关H课是否真的“不限优秀率”,我先后向数院负责管理华班的老师以及jwc负责成绩管理的王晓荣老师求证,得到的答复均为没有这种说法。(下附截图为jwc王老师的回复)
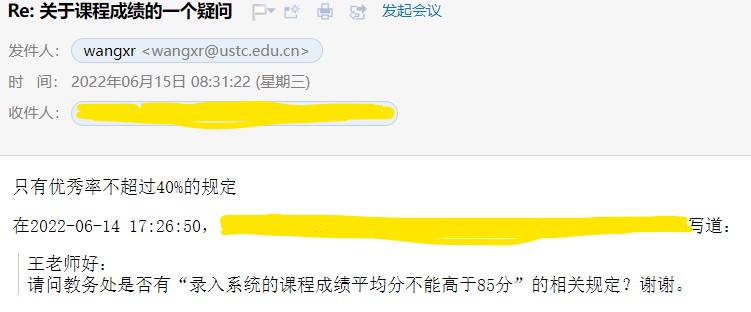
不过最后给分还是很不错的。
2023.06.23 更新:
这学期选了调和分析,期末被gank了,恰逢今年实分析H期末出成绩,特地在此破个防:
2023.07.28 更新
怎么到现在还有人总觉得H课就理应给多高的优秀率啊,又动不动就说优秀率给高了教务处不给过什么的,是有迫害妄想症还是咋的,,,最近水群又听说去年“被驳回”实际上是助教把总评给好之后任爷觉得大家考得也没那么好不想给那么高才这么说的,而且我去年就问了并且在这条点评里也写了教务处根本没有这种规定,自己选择性失明还赖教务处,教务处才没那闲心管你均分多少呢(当然这不影响教务处没ma的事实)
反正任爷,助教,教务处当中至少有一个人没说实话,你们自己猜是谁吧\偷笑
- 课程难度:简单
- 作业多少:很少
- 给分好坏:超好
- 收获大小:一般
- 难度:简单
- 作业:很少
- 给分:超好
- 收获:一般
想了想,还是给了十分。
任爷在今年还愿意重新回到黑板上讲课,并且之前的小测和点名应该也没有对成绩产生影响,在给分上也没有为难大家,又何必对一位教了三十多年书的老先生要求如此之高呢。
课程内容前人已经写的很多了,客观来说任爷对实分析主线把握的还是不错的,勒贝格可测集-可测函数-积分-微分。当然我认为这点内容应该只占实分析H的一半,当然剩下的我由于本身也不是做分析的,也没有读过别的实分析书,就不做评价了。任爷花了很多时间在控制收敛,交换次序这些东西上,不过这些东西其实这学期我也在很多概率课上用了非常多次,所以这些东西我认为也是有价值的。
作业质量太低也是这门课的一个问题,再怎么样也应该stein和zmq结合起来做,zmq的题目实在品味太差。
考试的话还是基本背诵ppt,不过我期末两道题都没背到(好像在习题课那节的ppt),不过也在考场上现场弄出来了,这边建议想拿高分还是得背的更熟一点。
给分的话个人感觉还是超级无敌奶,获得了上大学以来第一个满分总评。
唉还是希望这门课能上好的。
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:一般
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:一般
cy,看看接下来还有什么精彩操作
二编:改成全板书上课了,还是能听进建议的
比较意外地,后续任爷彻底白化,一直到期末再无点名,说的三次小测也没测,并且坚持使用板书。给分应该也是不错的,我小测没去期末比中位高9分也是捞到95了。这样下来本学期任爷其实没什么可吐槽的地方了,遂上调至10
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:一般
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:一般
实分析这门课确实展现了分析的很多经典思想,比如说“好+小”、从“原子”(特征函数)到一般可测函数等等,然后Vitali覆盖等小工具的使用也比较有趣。感觉这门课脉络还是很清晰的,比隔壁复分析好多了。
从课程内容来说,其实这门课有点低于我的预期,作为H课感觉讲的东西也不算特别多吧,由于没看过普通班的大纲,所以我也不清楚比普通班多讲了哪些东西。不过在以前实分析还是4学分的时候火箭带过,其课程主页上挂了当年讲义,讲了很多东西(感觉至少比这门课多了四分之一),如果还想学的更多的话可以看那份讲义(讲义Link:http://staff.ustc.edu.cn/~wangzuoq/Courses/18S-RealAnalysis/index.html),也可以去看Stein和Folland上的一些没讲的东西。
然后其实任爷对着PPT这种讲课方式我也不太适应(没上过数分A,之前没体验过),一门数学课还是有板书才有感觉。至于喜欢谈一些思想性的东西,我觉得没什么不好,毕竟分析学科确实要先有一些感觉才能去做具体的操作,不过讲这些的时候我喜欢走神就是了,不知道大家是不是这样。
这门课作业不多,基本来自周民强的书,前四章网上也可以找到答案,大部分难度不大。
今天期中期末都考完了,谈谈考试。根据做往年试卷的体验,今年的考试难度肯定是比往年低的,甚至可能比普班的简单。期中期末基本都是有大概四五十分PPT上的内容(包括某个命题的证明,或者是一些经典的例子和反例),如果把PPT记得比较牢的话这些部分可以快速写完。然后还有大概一两道很简单的题目,基本上就是顺着题目验证就可以的。所以有很多的时间处理剩下的比较新或者有一定难度的题目,基本上也就靠这个拉开一些差距了(还有你是否记得PPT上的内容)(吐槽一下期末最后一题是zmq正文的一道题目,没见过感觉很难想到怎么做)。总而言之,考试比较水。
最后期中97期末100总评100。
这门课真还是挺水的,无论是讲课、作业还是考试,作为H课这样有点不应该。
不过给分真的好到爆了,优秀率直接开到了65%,如果冲着这个来选课的话确实是相当好的选择。
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:一般
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:一般
实分析H还真有点是水课,虽然我学的不好,但平时尤其是期中之后真没花什么时间学过这门课。给分肯定是H课里很靠前的水平了,所以我觉得很多同学青睐于选H课也是无可厚非的,无论水平是高是低肯定还是有追求高绩的理想,这应该说是没问题的,但今年可能H班的水平确实比往年要低了一些。
体验的话也是不痛不痒,任爷的课比较提纲挈领,可能因此也有一些独属于任爷的话术。提纲挈领没问题,但是用ppt上课的话我觉得还是少了一些数学课的感觉,这是一个问题,并且内容确实并不多,期末前几天突击背诵ppt的话对应付考试基本是够用的。考试题的话感觉和zmq的题差不多,并没有太多营养,这可能也是一个问题。
- 课程难度:中等
- 作业多少:中等
- 给分好坏:一般
- 收获大小:没有
- 难度:中等
- 作业:中等
- 给分:一般
- 收获:没有
教材是周民强,一本陈旧而标准的教科书,正如作者所在机构北京大学的培养计划一样。如果你实分析只会周民强上面的内容,那么你还活在二十世纪上半叶。
实分析这门课,在后续学习中我只在动力系统课程中用到了其内容,在我的研究方向中完全没有再出现过。如果还在背诵周民强,还不如取消。
华罗庚会多复变,但不会在1963年(文革之前三年)就已经成熟了的微分流形理论。所以华罗庚没有资格搞复几何。
华罗庚班真是个笑话。15级数院很多厉害的同学们,比如姚院士,主动不加入华班的。
- 课程难度:简单
- 作业多少:很少
- 给分好坏:一般
- 收获大小:很多
- 难度:简单
- 作业:很少
- 给分:一般
- 收获:很多
任爷经常在课上用一些很好玩的比喻去描述实分析中的一些概念,令人印象深刻。这学期期中期末考试等于背书大赛,准确的来说是背上课内容大赛...,出题确实挺费心思的,但是两次都是背书大赛就一点意思都没有了。另外,球球任爷实分析多讲点东西吧orz
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:很多
对不起
中位数4.0
任爷你是神!!!
考勤和签到是应当的!
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:很多
先捡着优点说吧,任爷上课总是先把整个框架展示出来,再在后续时间里慢慢填补,对于小白来说确实很好接受,上课跟上也完全没有问题。而且任爷本来也很有人格魅力,自己期中考炸之后去找他聊天,给了很多指导(虽然自己没几项做到了),而且很鼓励我这个垃圾转院人学数学。哭死~~
但任爷的PPT确实很简略,假如考试按照PPT上写,要被扣惨。。。。而且上课花在一些“框架”上的时间有点太多了,整体显得华而不实。
有没有一种可能,H课比普通班更适合没什么基础的人。。。(迷惑)
- 课程难度:中等
- 作业多少:很少
- 给分好坏:一般
- 收获大小:一般
- 难度:中等
- 作业:很少
- 给分:一般
- 收获:一般
数分A1就是跟任爷上的,感觉任爷算是进入大学为我揭开数学大门的第一个人叭。这门实分析的话,感觉任爷功底很足,但讲课确实站位较高,相对来说细节就没有那么详细。所以可能提前学过一点或者预习到位的话听起来就会非常地爽。给分的话,还是比较友善的,本人期末一道大题看错题目导致卷面分没上80,但任爷还是奶上了优秀(虽然最初还是想上90,奈何发挥不行)。美中不足的就是由于疫情影响,线上上课,任爷课后也没有答疑的机会,助教习题课也就期末前上了一次。
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:一般
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:一般

效率很高,昨晚查的卷今天就出总评了,满意但还是有些小小的遗憾吧(期中不够高导致的~
整体一学期的体验还是很不错的,较之普班前半学期多了一些集合论的内容(神秘连续统基数),后半学期多了一些测度分解的内容吧,任✌也十分听劝的后半学期改成了全板书授课,对于一个教书几十年的长者,这无疑是值得尊敬的
考试方面个人感觉比普班卷子简单,背熟PPT就能拿到一个不错的分数(非常适合考前突击),给分虽然没有前几年那么超标但还是一如既往的奶,非常推荐习惯速通又想拿一个好成绩的同学来选(代价就是实分析a.e.没学会吧,缺的这块得靠高实了qwq
- 课程难度:中等
- 作业多少:很少
- 给分好坏:一般
- 收获大小:一般
- 难度:中等
- 作业:很少
- 给分:一般
- 收获:一般
实分析课程不是水课!不是水课!不是水课!重要的事情说三遍!!!
虽说任爷下半学期改用板书上课,但我还是难以跟上,再加上PPT以及zmq糟糕的可读性,感觉一学期下来没学到什么东西,甚至不如普班。
本来说有三次小测,一次都不到直接挂科,但最后只小测了一次,而我又没去,导致后面每节课都因为可能小测不得不去教室坐牢,体验非常差。期中最后一道20分题据说是小测原题,可能是变相扣平时分吧。
优秀率应该是和往年差不多,但优秀以下调分的力度似乎不大,反正我的成绩低于预期,可能准备二周目了。总结一下,如果水平还可以而且相比学到的东西更看重成绩,可以无脑选H班,其他还是好好斟酌一下吧。
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:一般
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:一般
先插个飞雷神标记🤣
尽管rgb回归板书授课 但我需要泼一盆冷水:板书与ppt不是重点 重点是推导过程能否详细写出 从目前来看rgb的证明过程还是一如既往的抽象,口述化 需要进一步观望
不过为rgb作出改变这件事,愿意给他一个10分
贡献一个低分段样本:63+65拿到3.3,拿3.3最开心的一次 期中期末全部大寄
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:一般
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:一般
7.9出分补:期中83期末86,最后93分。任爷的给分又一次没让我失望。
多少有点不礼貌了 晚起了十分钟就要吃3.3吗
更新一下评分:任爷+10分 助教+10分 私募教务处抓到课率-10分(你以为为什么会有小测和签到 不都是私募教务处天天搁那嗯抓到课率)最后十分 等期末考完细细评价
本课程今年的优点和缺点,其他人已经说的很清楚了。这门课确实有很多方面的缺陷:内容太少,有些看起来很有趣的内容只是一带而过地介绍(如符号测度、复测度那一节,如果想细细学习可以看Folland第三章),习题基本是周民强第四章的覆盖。任爷也是老教师了,可能人老了就喜欢絮絮叨叨一些思想性的内容?但是教学上还是没什么问题的,可以做到你一点就通。
总之,像其他两门H课一样,这门课也会有人喜欢有人不喜欢,比如我本人对PPT教学并不抵触,且数分A1就粉上了任爷,所以才来选课。如果有人想选,就可能得提前考虑好自己是否适应这种教学方式。
今年教务处似乎开始抓本科生到课率,不知道是任爷自己想搞还是教务处要求,今年多了三次小测和一次签到,但由于小测为开卷而且不看正确与否,所以实质上是四次签到。缺了的话可以通过期末做附加题来弥补。如果明年选课人数回归正常(今年这种显然是过热了,有很多人可能都是被去年的给分吸引而来),可能便不会有这种政策。
希望这门课能越来越好。
- 课程难度:简单
- 作业多少:很少
- 给分好坏:超好
- 收获大小:一般
- 难度:简单
- 作业:很少
- 给分:超好
- 收获:一般
第一次写评课社区,各方面的评价可能比较主观,大家多多包涵。
实分析(H)这门课程主要的内容如下:
主线:集合论→Lebesgue测度论→Lebesgue积分论(PPT 2-16+20-21)
支线1:抽象测度与积分理论(PPT 17-19+22)
支线2:Lebesgue框架下的微积分基本定理 (PPT 23-26)
支线3:L^p空间理论(PPT 28-29)
每一部分的详细介绍与核心内容可以去看田助教的详细介绍,这里不再赘述。
不得不说,任爷对于主线和支线2的把握还是相当精彩的,内容有深度又通俗易懂,紧跟老师步伐弄懂PPT上的内容应该不会落入“实变函数学十遍”的囹圄之中(但是两三遍似乎是有必要的);但是支线1和支线3可能因为课程安排与时间原因讲的不是很详细,许多内容只是介绍性质的(当然抽象测度这块儿似乎考试考都没有考),不过这里还是建议大家多去学一些,可以参考Folland书上的相关内容进行补充(至少我个人认为该书上用支线1的知识去证明支线2的里面命题的过程是相当精彩的)。
教材方面,个人不建议使用周民强的教材进行自学(尤其是第一遍),感觉逻辑有些混乱。我自己学习本门课的路线是:寒假的时候先找网上任爷往年的课程视频听一下,了解个大概,适应了之后直接看Folland书。
助教方面,懂得都懂,个人能力强大不堪,而且感觉与带数分A1时候相比仁慈了不少吧(笑)。可能是因为毕业和出国相关事宜吧,这学期的习题课比较少,而且大部分时间讲的都是拓展内容(比如说Hausdorff测度和谱测度),其实还想听田神讲更多拓展内容的!!!希望明年的助教可以继承田神的精神~
考试方面其实我个人有点小小的不满意,其实我个人不太好评价“PPT默写”式的考试对于促进课程学习的效果如何,但是至少从最后的总评给分来看算是皆大欢喜(班级里面一半的同学拿到了满绩点)。
总的来说,我对于实分析(H)这门课程的整体评价还是很高的,但是内容设置上和考试题目设置上可能还是有一定的改进空间,所以打9分。内容方面,如果任爷还是不发生改变,讲的比较介绍性的部分可以通过自学弥补(或者求助教浇浇);而考试题目设置方面,或许会因为助教的变化而发生风格上的改变(这两年都是田神给任爷供题任爷略作修改,不知道明年会如何),这些就靠之后的大家了!
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:很多
任爷的讲法可谓是高屋建瓴、大道至简。这个学期很多课像听故事一样就过去了,一回头看ppt才发现讲了好多。 ts当助教也很耐心,我提的多蠢的问题都会一步一步讲解 ˉ﹃ˉ。改卷的时候放洪水。这个学期遇上任爷和ts不可不谓是一种幸运。 考试题目几乎是见过的,大多来自ppt、作业、习题课,期末会有一道稍难的。两次考试都是一道题错了就直接下中位数_(´`」 ∠)。最后原始分就很高所以没怎么调。虽然大半个班都得了较高绩点,但是苦了一些没考好的,没调分导致出来就很低。
- 课程难度:困难
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:中等
- 给分:超好
- 收获:很多
先来占个坑
这学期依然是ppt授课(那看起来以后都是ppt了),板书“差不多”是没有的。任老师讲课是很有特点的,能经常讲授数学思想,但其实我个人感觉这是一把双刃剑。。。就有时候课上空话套话稍微有点多。
然后个人还是感觉在ppt上做数学证明不是一种最好的方式。如果硬要用ppt,私以为权宜之计是一行一行地放出证明,而不是一下把证明全放出来。。。
另外还有一点是上课详略稍有失衡,一些例子虽然简单,但是却花了很长时间讲解;而一些证明比较抽象、困难,却只有干巴巴的文字(当然可能只是我太菜了😂
非常喜欢板书授课的同学,上述个人感受可能有小小的参考价值👻
期末出分了。给分是真心好,期末在平均90左右而我错了十道题里两道题的情况下仍然能给优秀。。。
下半学期的观点确实高,但自然细节就相对少了,看个人喜好吧
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:很多
我大三下,由于需要复习一些实分析的知识,选了李皓昭老师的班,两个班我都有比较,我认为任老师的这个课是很有意义的,他在分析的具体细节上也许讲的不是那么多,但是在整体框架的把握上,我认为做的非常好。而且讲解的内容很具有拓展性,比普班的内容是要多得多的,但可能在某些细节的处理没有那么细,需要感兴趣的同学自己去看书,给分当然是很好啊,当然,普班我觉得今年给分也挺好的。考试难度不是很大吧,至少我认为稍微花点时间拿个3.7是没有问题。
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:一般
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:一般
多年以后人们或许会忘记实分析的知识,但不会忘记任爷的“实分析双子塔”,“实分析大楼”,“仿生学”,“分析是极限的艺术”,甚至这些话语会在意想不到的瞬间浮现在脑海中。
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:没有
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:没有
事少给分好,值得6分。
希望少一点时间务虚,有些内容还是比较复杂的。PPT上某些难题,若解答过程简略,所列“要点”令人困惑时,常常能在周民强书上获得答案。
看任老师在本社区有极高评价,然而在该课程令人大跌眼镜,也许是用起了PPT?
任老师强调了几十次 Constantin Carathéodory 是天才数学家,但却在严谨的数学语境下拼错了他的名字。
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:一般
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:一般
前半学期的体验还是非常好的, 很清晰的构造测度和积分的主线, 特别是助教哥哥补充的从集类构造测度的一般定理给我一种我瞬间无所不能的爽感, 但是从这个主线结束就开始混乱了, 后半学期这边来点边角料那边来点边角料, 又什么都没多讲, 特别是卷积和 good kernel 这套东西竟然一点都没提, 包括 \(L^p\) 空间也是给了个定义就没有下文了, 再加上任爷特有的轻严谨证明重理解的讲法, 我基本全程蒙古, 不过也可能是我太菜了吧(
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:很多
虽然但是,这样强行小测是不是有点逆天了,我还没学明白呢硬控我两节课,最后糊了点交上去了
建议以后改为通知哪次课不小测😓
每节课开头都重复那一套😓
从备考的角度来看这门课确实很水,考前三天背一遍ppt就行了。一学期下来我的周民强还是跟新的一样,感觉可以转手卖了。这学期考试出的也并不完全是背诵大赛,不过ppt都掌握了拿个4应该问题不大。如果有时间卷的话可以看一下周民强,虽然这本书的排版实在劝退。比较奇怪的是我感觉期末比期中难,但大家的期末成绩却普遍比期中高。任爷讲课讲的最好的部分我认为是几种收敛之间的关系。复(预)习的时候再看任爷的ppt我发现内容还是不少的,只是任爷上课经常讲不完。我猜测主要原因是任爷目前使用的ppt是在20年疫情期间制作的,而从20年的回放来看任爷当时是调整了上课时间的,每次课都是2.5节。线下课是周一三节课,周三两节课,这就导致可能原来内容量平均的ppt不适合目前的教学。周一侃侃而谈的话或许尚能讲完ppt,但周三侃侃而谈的话ppt就势必讲不完了。不过也有好处就是迟到一会儿也不用担心跟不上。想想后面周一竟然能抽出来一整节课来小测就知道任爷其实是可以讲的快的。这学期助教很负责,详见dhgg的评课。如果想学更多干货的话习题课讲义内容也很丰富,不过我确实没时间看了。但是从某种程度上助教的过度负责或许也使这门课更加水了。比如可以直接把助教写的作业答案交上去。总体来说这门课所花费的时间可控且给分好,付出与回报呈正相关,推荐选课。
- 课程难度:困难
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:很少
- 给分:超好
- 收获:很多
实分析的双子塔:测度论,积分论
分析是极限的艺术
测度可以视为积分,积分也可以视为测度。
好了,实分析学完了(bushi)
原本以为PPT式教学会导致课堂笔记做不完,但任爷对节奏的把握总能让你及时补完笔记并且弄懂(
任爷所用的PPT应该是用了很多年了,每年都会对一些错漏作出修改,但所有内容关于时间保持a.e.相等,在孙天阳学长的主页里或者是西瓜视频(田神说的,我也没有考究过)都有任爷往年的录课,要是想提前学习实分析,可以去听一听。
PPT主打一个简洁,一面PPT的字寥寥无几,但是足以概括整个定理的证明。这样做的代价是,自己看PPT弄懂的时间要比上课听讲弄懂的时间还要长,而且有些具体的细节还需要课后进行补充。PPT的证明和例题大部分来自周民强的教材,或许是因为我之前看的是stein,因此对周民强还不太反感(?但是stein写的是真的抽象。
任爷讲实分析的思路主打一个体系建构,这是上其他数学课从来没有的体验,对于我这种喜欢搞体系结构化学习一门课的人来说再合适不过了。从关联测度论,积分论的大体系,再到重要定理证明过程的结构化思想(打包研究目标集合,积分经典四步走,提取微积分基本定理背后的商集对应等等),个人认为这样的学习才能真正把握一门课的脉络。当然要想更深入全面地学习实分析,还得是看Folland。
关于作业,周民强上的题比较适中,例题有部分比较困难,但是相比于stein和Folland上的习题可以说是没什么营养。要想在做题过程中领悟题目的真实意图,可以做stein的习题。不过考试(包括H和普班)的命题风格跟周民强贴近,这点需要各位自我权衡。
考试不必多说,考试的形式决定了这门课可以是相对轻松的课,但是容错率也会大大降低,平均分会很高,一题错了就会到中位数。助教改卷也主打一个尽量捞分,希望这个传统可以继续延续到以后的实分析H课上,造福广大生存不易的花瓣学子。
- 课程难度:中等
- 作业多少:中等
- 给分好坏:杀手
- 收获大小:一般
- 难度:中等
- 作业:中等
- 给分:杀手
- 收获:一般
老师是好人,助教也尽力捞了。
只有jwc是啥比!!!
- 课程难度:中等
- 作业多少:很少
- 给分好坏:一般
- 收获大小:一般
- 难度:中等
- 作业:很少
- 给分:一般
- 收获:一般
任爷水平还是高的,另外这学期的李助教必须点个赞,非常负责,习题课,作业考试的批改都非常认真。
扣两分一分扣在用ppt上,ppt的上课效果实在有点一言难尽。另一分扣在周民强这本书上,个人对这本书实在是深恶痛绝,正文中间穿插着一堆杂七杂八和正文没啥关系的例子和习题,使得主线很不明确。课后题目是很多,但做作业的时候感觉很多题目质量很差,有点强行拼凑或者意义不明的感觉。
给分:今年考试比较容易,期中很简单,90多甚至100者众,期末加大了难度,但也并没有难到哪去。因此最后没有调分(可能捞了一下卡绩的人),但最后大家考的都很好,优秀大概有30人左右(一共也就40人不到)。另外今年明显是助教出题(至少大半是助教出的),很多题目是从Rudin,stein之类的书上摘的,明年换成任爷自己出题的话情况可能会变化。
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:一般
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:一般
本人不太适应任爷风格。。。
话说任爷在疫情那学期之前应该不用PPT吧,这学期是不是有了PPT之后变懒了。。。(悲)
任爷的水平绝对是高的,但我觉得介绍性、框架性的内容的比重对初学者来说偏大了,一些细节不太到位。
不过任爷讲课速度确实不快,因此可以Stein和Folland同步跟着任爷进度。。。
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:很多
既卿爷以后第二个让我佩服的不行的老师,真的有这样的老师能让你觉得呆在科大是一种幸运。给分讲课都超好,自不必说。
- 课程难度:简单
- 作业多少:很少
- 给分好坏:超好
- 收获大小:一般
- 难度:简单
- 作业:很少
- 给分:超好
- 收获:一般
尽管任爷今年讲课挂黑板频率高了,不过毕竟任爷水平还是很高的,讲课大部分时候还是行云流水,非常舒服。
- 课程难度:简单
- 作业多少:中等
- 给分好坏:一般
- 收获大小:一般
- 难度:简单
- 作业:中等
- 给分:一般
- 收获:一般
感觉还是比较看期中的…一节课没来,期中大寄55 期末94无力回天 吃3.7 虽然基本都是ppt背诵但我还是太菜了
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:很多
也许永远抱着半吊子心态就注定伴随着卡绩瓶颈…但成绩之外,这门课还是让我获益匪浅,尤其抽象积分那一部分可谓述尽分析的美。PPT难免有不够详尽的地方,不过前半学期基本上和周民强相结合即可互补,后半学期有来自Folland的及lieb的部分可以参考原书。总之是非成败转头空,还是很感谢任✌🏻以及助教学长。
期中考最后一题似乎是小测原题,尽管是在理论上的考试范围之外——PPT15里。
感觉任老师偶尔有些头脑不灵光了,作为知识分子惯有的小傲娇又不离不弃,还是希望同学们可以宽容一些吧qnq
- 课程难度:困难
- 作业多少:很少
- 给分好坏:超好
- 收获大小:一般
- 难度:困难
- 作业:很少
- 给分:超好
- 收获:一般
任✌️的奶力都捞不回来我,我是不是没救了😭)
作为一个并不擅长也不太喜欢学比较抽象的数学的人,我选H单纯是因为任✌️的给分还有强基的要求。但是学了之后才发现,我能做的只有不断的看之前录课把PPT里每一个不懂的地方稍微搞懂一点,理解PPT里最浅显的思想罢了,考试两次都没到平均分,也是意料之中。
最后提醒一下之后的强基生,如果你打算走计算方向,是不需要选两门H的)
- 课程难度:简单
- 作业多少:很少
- 给分好坏:超好
- 收获大小:一般
- 难度:简单
- 作业:很少
- 给分:超好
- 收获:一般
这门课确实存在着一些问题,PPT过程简略,任爷上课也确实有些“侃侃而谈”,以及为了到课率而连续小测签到。记得第一次小测是早八,那天我起得挺早的,不过到了教室也过了七点半了,当时从后门往里一看发现整个教室只有任爷一个人,一方面感叹任爷对教学的热情,另一方面也觉得这个到课率确实感人了🤣,果不其然就小测了(现在回头想想发现任爷每次课都是提前挺久到的教室,貌似从来没有压点或迟到过,对教学真的是很上心了,站在任爷角度想一想,不管是谁遇到这种满怀热情走入教室发现空无一人的情况都会挺失望的吧)。
关于授课内容和PPT,其实我感觉这个PPT还是说得过去的,过程简略实际上省掉的大都是一些比较公式化套路化的东西,转而将其用一种概括性思想性的语言表达出来,其实读起来也不会有较大的阻碍,不过也可能是因为我去年在普班学过一遍实分析)说到这就顺便来比较一下普班和H班的内容吧,个人感觉任爷PPT作为H课确实内容稍有点少了,没觉得比普班多讲了很多东西,一些拓展内容也是点到为止,当然考试也不会涉及,最后很可能是教过就忘)但总体内容也绝不至于比普班少,也还是够用的。
再到后来任爷把PPT换成了纯板书,虽然我觉得这样讲课方式和风格没变化,写板书还不如PPT放得快,反而拖慢了进度,但是任爷愿意为了提高教学质量作出改变,凭这份对教学工作的热情,我觉得任爷值得我打10分。
最后考试和给分还是一如既往地奶,不过比较难绷的是期中最后一题是期中范围外的PPT上的原题,且是小测原题,小测时没听直接抄PPT了,考场上脑子也卡住了没想起来,爆扣了十几分🤣,并且前面还考了20分概念题,有点神秘了,送的20分也没拿全,最后喜提81,期末94,总评也是给捞到4.3了,神!
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:很多
转数人一枚,有幸成为任爷的学生。
ppt主要参考folland,课程主线与zmq差别挺大。大致框架是:基本集合论,抽象测度,Lebesgue可测函数,Lebesgue积分,抽象积分,Fubini定理,微积分基本定理,Lp空间。许多细节也采用了与zmq不同的方式处理。笔者由此认为教学内容与若干年前已经有了很大调整。作业依旧是布置zmq的习题,这一点将来也许可以改进。
任爷的课堂引人入胜,一学期下来获益良多,就是上年纪了,一些例题容易挂黑板(乐)。这节课其实不需要太多前置知识,给分也是极好的,属于是老少咸宜了,对自己有自信的大一学生可以尝试大一下就把任爷的实分析选了。不过假使有人能继承ts的伟大精神,以后这门课可能会一位难求hhh。
最后说一下听这门课比较遗憾的点吧。首先是积分本身与泛函有着千丝万缕的联系,囿于知识所限,这门课对此只能做到一点点科普。其次,在抽象积分这部分,不少重要的结果只给出了证明的部分或者不予证明,笔者翻阅了folland的对应章节,私以为无论是难度上还是篇幅上都是可以做到完全证明的,略有遗憾。不过教学内容仍旧是瑕不掩瑜。
- 课程难度:简单
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:简单
- 作业:很少
- 给分:超好
- 收获:很多
任爷数院同学都不陌生,上课主打接地气理解记忆法,摒弃了毫无直观可言的部分。
上课采取的是高观点讲课,低难度习题的策略,非常非常舒服,比隔壁复变函数好太多了。(史济怀复变教材习题太难了)
由于任爷PPT制作的独特风格,一开始可能不太适应他上课的ppt形式,但差不多过了6个ppt以后就能轻车熟路了。(不过ppt有点简略,没有适当笔记不具有可读性)
考试方面,同时感谢助教田神,出题心慈手软,都是些应知应会的东西(PPT里的),可能比较水(简单)?但毕竟是H课,教啥考啥应知应会。(不喜欢专门用来区分同学的压轴题,对于一道题,如果只有一半人做出来,那是老师上课没教好还是这部分人靠聪明才智胜人一筹?那要上课何用?)
期中中位数92,期末中位数90,皆大欢喜。
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:一般
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:一般
听任爷上课很舒服,看ppt虽然有些地方没写细致,但上课听过之后再复习也是想的起来的。而且本人不爱做笔记,所以ppt对我来说影响不大。 课程内容确实不是很多,真包含于zmq,第六章Lp空间那里只讲了两节课,最后甚至能够提早一两周结课,真是给足了复习时间。 给分超好这点是公认的了,本人期中比均分低了4分,期末只比均分高了5分,最后总评拿了90,任爷yyds。
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:一般
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:一般
说实话,一学期上下来收获不大。任老师是ppt教学,上课就像听讲座一样,很多东西也没有对应的课后题。就算听课,也没法巩固。期末考试的题目也有些难蚌。这学期基本都靠自学,不过给分挺好的。
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:很多
第一次遇见主要靠ppt而不是板书的数学老师,还是有些不习惯,个人还是更喜欢板书教学。然后好像所有人都在说这门课简单,菜鸡哭了。
助教超级好,每周都有习题课,补充很多内容,每次都是两个多小时,可惜我比较菜,基本上一个小时之后开始懵逼,大概也是习题课人数随周数递减的原因。
给分没得说的,优秀率接近70%,期末低了均分近10分都打算重修了,老师硬是把我捞上了优秀。
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:很多
大一的时候上了任老师的数分,那个时候就很喜欢任老师上课的节奏和板书,或者说对于任老师上课的高度很崇拜。于是一直期盼着上任老师的实分析课。其实上第一节课的时候,任老师用ppt过了一遍实分析大概的内容,那种感觉就好像又回到了大一上第一节课的感觉。
第二节课的时候任爷上课还是用ppt,那个时候还有一点失望。毕竟很大的程度上是冲着任老师的板书来的,但是听了几节课之后,慢慢的也就适应了任老师上课的节奏。对于一个证明任老师还是讲的很细的,就是有点快,如果要记笔记的话,那就有点考验手速了。哈哈。但是任老师讲完一个定理之后就会问同学们有没有问题,其实我感觉这样挺好的。
另外我感觉任老师最厉害的地方在于对于实分析内容的理解高度。任老师应该是教了很多年的实分析了,各种原本抽象的东西在他心里可能就已经变得很直观很具体,而且可以把它讲出来,这是我非常佩服的地方。个人感觉像数学这种抽象的语言,如果心中没有一个大致的轮廓,很快就会忘得一干二净。任老师给予了数学概念另外一种身份,其实是很有助于记忆的。不过任爷每一次上课都会重复之前的概念,前面几次可能还好,加深印象,但是到了后面阶段,感觉有点迷。。。难道这就是所谓的‘实变函数学十遍’??
至于作业和考试,作业很简单,没意思,感觉隔壁班的作业还要难一些。考试的话,期中挺简单的,有些困难的题有提示。期末有点难,没考完,不过貌似改的挺松。。
给分挺好的,最后感谢任爷抬了一手,在卡绩边缘捞了我一把,orz。
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:很多
教材是周民强《实变函数论》,强哥的教材特点是例题难度大,不过对华班可能正合适。任爷特别喜欢这本教材,备考只要做书上的例题和习题就好了。这学期课时比较充裕,老师补充了抽象测度,这部分可以参考徐森林老师的同名教材。
任爷的课最大的优点就是主线明确,从零开始构建实分析“大楼”,其中核心的内容是什么,每定理位居何种地位,不同的定理有哪些内在或外在的联系,老师上课会反复强调,直到你理解为止。其次,任爷上课行云流水,每一步都知道要干什么、为什么用这种方法、其中蕴含了什么思想,都给你解释的很清楚。这学期学了很多数学课,听任爷讲定理的证明是最舒服的、是永远不会犯困的。任爷不会难为学生,作业少而精,期末考试题目都比较基本,助教讲了一个挺难的例子被老师删了,最后给分也很好。
虽然拓展的东西不多,但是听课比自己看书舒服太多了,本来有一定难度的实分析被教成中学生都能理解的难度。这是一种高超的教学艺术,是大多数老师想讲而讲不出来的。听任爷讲课可以帮你把自己看书“百思不得其解”的时间节省出来,用来学自己感兴趣的东西,这才是基础课的最高境界。如此鉴课居然连9.5分都不到,米娜桑是不是有些要求过高了。
- 课程难度:简单
- 作业多少:很少
- 给分好坏:一般
- 收获大小:一般
- 难度:简单
- 作业:很少
- 给分:一般
- 收获:一般
任老师拿ppt上课,这点我不是很喜欢。ppt这东西翻得很快搞得不好记笔记,证明也过的很快。这多出来的时间老师比较喜欢拿来讲理解,但是讲来讲去很多东西都是复读,有这时间还不如把证明详细讲一讲呢。
另外上课的内容也emm。周民强那本书的内容较Stein单薄了一点,像是littlewood极大函数我们没讲,普通班倒讲了。还有抽象测度那里讲的也很模糊,有些证明不是很严格的样子。而且作业也太简单了,绝大多数都是在套公式,一点分析的意思都没有。
- 课程难度:简单
- 作业多少:很少
- 给分好坏:一般
- 收获大小:一般
- 难度:简单
- 作业:很少
- 给分:一般
- 收获:一般
因为之前没有上过任老师的课,所以不是很清楚任老师的上课风格。这学期的实分析H因为疫情上的是网课,任老师上课用的是ppt,但ppt上的细节严重不足,大多需要老师在ppt上手写补充。
另一方面任老师上课的速度个人感觉非常的慢,导致进度比普通班慢了很多很多,不过在后期用一节课(如果没记错的话)讲完了大部分抽象测度内容,但老师还是补充了很多有意思的例子。因为我很早就自学过实分析,所以我大部分时间只是开声音挂着直播然后刷手机,或者在周四和微分方程2H冲课的时候关声音去听微分方程2H。(为什么不直接不听是因为怂,担心自己漏掉一些细节orz)
考试的话很多人都已经提过了就不再提了,很简单,但还是zz错了几处细节(比如非常简单的积分计算)导致最后被卡了94(虽然一分没调很难受,但是因为错的题实在是太zz所以认了orz)。
- 课程难度:中等
- 作业多少:很少
- 给分好坏:一般
- 收获大小:一般
- 难度:中等
- 作业:很少
- 给分:一般
- 收获:一般
我是20春在家上的网课,,,
因为无法板书,任老师全程使用了PPT(但并没有发给同学,好像是担心泄露,无可厚非吧)。我因为很早为了学概率论、泛函、方程2等课,1年前就自学过了实分析,这学期网课事实上也没怎么听,,,
最后期末考了10道题(各10分),准确来说不难。我大概1小时出头就写完了9道,剩下一道“证明R中非空完全集不可数”这道之前的作业题想不起来,盯钟发呆了几十分钟。。。
后来出分,借着作业分刚刚好往上提了一档,应该算相当圆满了。
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:一般
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:一般
讲了的部分讲得很清楚,但是内容不是很多
- 课程难度:简单
- 作业多少:中等
- 给分好坏:超好
- 收获大小:一般
- 难度:简单
- 作业:中等
- 给分:超好
- 收获:一般
学过的课里面觉得上的最好的老师,没有之一
老师把所有的细节和思路,以及为什么要这样做讲的清清楚楚。而且不知道为什么,有一种高中老师上课的感觉,可能是他上这课已经上了无数遍了吧。
只要认真听课,感觉不写作业都没问题,唯一的问题就是讲的有点少,不过按照他的意思,后面有些内容不去在后续课程中系统的学,现在蜻蜓点水点一下也没有什么卵用,索性不讲。
最后,给分超好
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:很多
任神讲课不带课本,行云流水。
经常给学生梳理知识体系,构建一个完整的知识框架(实分析大楼)
中间穿插周易,庄子
给分超好,不卡g点,总评绝对出乎你意料。
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:很多
教材是周民強的《實變函數》。其中,第五章的5.5和5.6兩節沒講,而第六章只講了6.1和6.2中的完備性。(H班比隔壁王火箭和麻方程講得少)大概15周就結課了。
老師講得很好。作業大概是每週8道題。
期中考大放水,2小時6道題,平均分接近90;期末考提升了難度,2.5小時10道題。
給分好,總評91,比較滿意。
2019/3/1 講的少了點,建議自學folland。
- 课程难度:困难
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:中等
- 给分:超好
- 收获:很多
我觉的讲的挺好的,老师理的很清楚,不是全按课本讲,不带课本讲课(很强大),给分不错。数院男神。