2021秋 2020秋 2013秋 课程号:00135502
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
| 选课类别:计划内与自由选修 | 教学类型:理论课 |
| 课程类别:本科计划内课程 | 开课单位:数学科学学院 |
| 课程层次:专业基础 | 学分:4.0 |
教材:丁同仁,李承治《常微分方程教程》,第二版
谷超豪,李大潜 等《数学物理方程》,第三版
韩青,林芳华:Elliptic Partial Differential Equations, 2nd edition
参考书:Lawrence C.Evans: Partial Differential Equations, 2nd edition, 2010
课程内容:
ODE部分:丁同仁第2~7章,8.1~8.3,9.1~9.3(第7章由助教在习题课上讲授)
PDE部分:谷超豪第1、2章,韩青林芳华第1章,部分结论的证明参考Evans 第2章
教学水平与课程内容
赵立丰老师在《微分方程I》的教学中展示了深厚的学术造诣和高超的教学水平,尤其在PDE(偏微分方程)领域。他授课条理清晰,除了讲解定理外,会深入解释背后的动机和构造函数的思路。但课程内容繁多,包括ODE(常微分方程)和PDE各半学期,时间紧安排密集,部分内容只能略讲甚至略去,使得学生必须课后加倍努力。学生普遍反映,课程开设内容丰富,学到了大量的微分方程核心理论和求解技巧。
教材与参考资料
课程使用的教材为丁同仁和谷超豪的著作,但部分学生觉得谷超豪的《数学物理方程》记号过于晦涩,因此赵老师也借鉴了Evans和韩青林芳华的材料进行授课,学生表示这些辅助材料帮助理解。讲课时结合了不同教材的优点,对教材内容提出了自己的见解,讲解的内容远超教材本身。
考试与作业
考试主要分为期中考(ODE部分)和期末考(PDE部分)。期中考重在计算,题量大,多为解方程和定性理论基础题;期末考则主要考查对定理的理解和应用,一道题包含了更多的证明要求。整体考题中规中矩,与教学内容高度相关。作业量适中,但因内容深奥,完成质量要求高,学习过程需要大量练习和推导。
给分与表现
赵老师以仁慈的给分方式著称,许多同学反映总评分数高于原本预期,极大地鼓舞了学生们的学习热情,即便期中表现不佳,经过期末的努力也有机会获得不错的总评。
学生建议
多名学生建议将课程学分提升至6学分以匹配实际的学习负担,并建议在教材选择上进行改进,以提升学习体验。整体而言,课程强度大,收益显著,但需花费充足时间实践计算、巩固理论,以将所学应用自如。
总之,《微分方程I》在学生中口碑极佳,尤其推荐对微分方程感兴趣、愿意投入学习时间的同学选修。赵立丰老师以其幽默和扎实的教学风格,被称为是这门课的亮点。
- 课程难度:困难
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:中等
- 给分:超好
- 收获:很多
这门课是我这学期投入时间最多,也是收获最大的一门课。
关于老师和助教:
赵立丰yyds
赵老师不管是学术水平还是教学水平都很高,非常负责,通过助教反映,觉得大家作业做的不行,每个星期基本上都安排习题课,而且据我观察好多习题课 赵老师都亲自到场,坐在后面听。为了鼓励大家上习题课的积极性,还特别强调期末会至少出一题习题课讲的题。 3位助教也超级负责,水平很高。尤其是邵锋助教,习题课行云流水,给人的感觉非常舒服。总之,以后选课 无脑赵立丰就对了。
下面说一下课程内容
这门课使用的教材上面课程简介已经说了,ODE部分按照丁同仁讲,PDE部分波方程和热传导方程按照谷超豪讲,调和方程按照韩青讲,所以调和这部分讲的有点深度,难度也大一点。
ODE部分是一些初等解法,然后就是定性理论,不过方程的重点并不是解方程,最精彩的还是定性理论,从解的存在唯一性定理将我引入大门,主要证法应该有: Picard逐次迭代,压缩映射,运用Gronwall不等式证明唯一性。这个定理的证明是需要掌握的。然后就是解的延伸,最大存在区间,我认为最大存在区间的题目是最难的,很多操作想不到。 然后就是高阶ODE,微分方程组,有一个利用根子空间分解计算基解矩阵的贼复杂的公式,背得就是。微分方程的幂级数解法,赵老师没有正课上讲,让助教通过几次习题课介绍,期中考试是6道解方程题里面选5到,有一道是必须用幂级数解法,最后进入第二阶段定性理论,稳定性(线性近似,Lyapunov),动力系统初步,初等奇点类型判断(要背). 这部分内容由于时间限制,无法讲深入。不过要恭喜学弟学妹,这门课将变成6学分。
PDE部分给我印象最为深刻的就是调和函数里面各种性质的讲解,motivation, 各种精妙的估计和构造,截断手法。涉及到平均值公式,极值原理,梯度估计,解析性,Harnack不等式,可去奇点定理,最大模估计,Hopf引理等等。
上图!

热方程主要内容有:
Fourier变换推导热传导方程基本解(Fourier变换法非常重要!!!),初值问题的解的衰减性,稳定性,极值原理,以及通过构造各种函数来运用极值原理证明边值问题解的唯一性和稳定性,这部分的证明也非常重要,需要掌握。
波方程的内容有:
1维的达朗贝尔公式,球面平均推导3维的Krichhoff公式,然后降维 打击 2维的Poisson公式,波的有限传播速度等
除此之外PDE部分还有 分离变量法 特征线法(一阶方程的解法很容易被忽视)也非常重要
谷超豪数学物理方程里面的有些记号实在是过于拉跨,强烈建议看Evans! 我考前一个多月,耗费巨量时间终于把Evans 第二章大部分内容都搞清楚了,里面的很多细节其实并不显然,需要认真check.
这里引用彦神的话:
这是本科阶段第一门具有较高强度计算量的课程,请同学们务必用手拿着笔在纸上计算每一步。否则失之毫厘,谬以千里分部积分不会,请对照附录、写成分量计算!
学这种高级课程才知道自己基础分析知识掌握的多么不扎实!多么不熟练!
2020年最后一节课结课时老师还是顺带着介绍了方程路线,需要学哪些分析知识,一些研究的前沿,让同学们知道PDE不止那3类方程,前沿在研究什么,还推荐了几本书供后续想学方程的同学学习。
推荐的书是:
1.Serge Alinhac , hyperbolic partial differential equations
2.Qing Han, Fanghua Lin ,Elliptic partial differential equations


老师长得也太喜庆了吧! 完结撒花!
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:很多
这门课大概是大二上数学系必修课里最“硬”的一门了。正如赵老师所说,这门课并没有多难,但内容比较多(半个学期ode半个学期pde),想要学好还是要下功夫的。
ode部分,我个人感觉是比较无聊的。老师上课讲的中(fu)规(du)中(ke)矩(ben)。因为时间原因,很多内容不得不一笔带过 ,但不管怎么样,学完ode,至少要了解ode的基本理论(解的存在唯一性定理,解对初值的连续依赖性,可微性,这些也是这门课的核心内容,要掌握推导过程以及应用),以及会解常见的方程。要适当做一些解方程的练习,防止到了考场上一算就错。
pde部分,最开始赵老师选择的教材是谷超豪的《数学物理方程》,这书实在是无力吐槽。一方面,这书写作风格给人感觉很不“数学”。另一方面,课本上的记号简直可以用灾难性来形容,已经到了严重影响阅读的程度。“我从来没见过用这种记号的书”(助教习题课原话)。于是我除了写作业之外就基本上没再翻开过这书。后来老师似乎也意识到了这个问题,上课也就没怎么按照书上来讲,而是参考evans和林芳华的书来讲授,体验要好不少。
抛去谷超豪这本书的问题不谈,pde部分赵老师讲的还是灰常清楚的,个人感觉比上半学期ode讲的要好。赵老师并不是单单把定理的证明写到黑板上,而是会把定理背后的想法,定理证明涉及到的关键技术都讲出来,而这些东西在进一步的学习中都是用的到的。另外三位助教也都非常负责,每周都会安排习题课,讲解一些补充内容。因此虽然教材有缺陷,但我觉得pde部分的授课质量还是配的上10分的。
关于pde部分的学习,首先必须要做到熟练地掌握多元微积分,分部积分,高维的Gauss- Green公式,熟练地进行球坐标的变换。这些是pde里最基本的技术,在学习过程中要用到114514次。因此如果数分A2学的不够好,就要在这些上面花点时间,通过计算来熟悉这些操作(可参考evans附录)。另外学习pde的时候我个人认为没必要花太多时间去做一些无聊的计算题(指谷超豪上那些分离变量法,是真的无聊,且最后考试也没怎么考),重点放在理解定理证明的想法,掌握定理证明的关键技术上,而这些东西也往往是初学者感到困难的部分。具体说来,在证明极值原理,Hopf引理的时候,要引进一些辅助函数。在用能量方法证明解的唯一性,稳定性的时候,要在方程两边乘一个因子分部积分,然后用柯西不等式放缩云云,得到能量的估计式。在证明调和函数的内部梯度估计的时候,引进一个截断函数f,然后计算f方Gradient(u)方的拉普拉斯,最终通过极值原理得到估计,这些都是学习时候要重点关注,课下要花时间去看的。除去听老师讲课,课下可以自己去读evans第二章(一些比较麻烦且不关键的东西可以跳过不读,比如n维波方程公式的推导),以及第六,七章里极值原理的部分,把主要定理的证明都给过一遍,这样我觉得就已经非常好了。
关于考试,期中ode考三个小时(两个半小时延长到三小时),满分150,重在计算,主要考察计算的细心程度,如果不慎算错可能要翻车,因此平常要适当做些练习,课本上一些公式最好也要背一背(考了一个大题,二阶非常系数ode已知一个解求另一个解,如果背过公式那这题就是秒),奇点类型的判定也需要背(我背了半天还是记错一个,淦)。关于定性理论的题目,一题老师上课讲过(Liapunov函数构造),出自Smale的书,考试时仅仅改了个数字。另外两题,一题证明唯一性,和作业大同小异 ,另一题出自课本S-L理论部分,只要你对ode的几个基本定理熟悉,那基本也没难度。因此只要考前认真复习课本和作业,考试时细心一点就可以拿到很好的分数。
期末考试,满分100,时间两小时延长到两个半,题目风格大变,只有五道题,比较“分析”,主要考察对上课讲过的定理的理解。考前请认真复习老师讲过的定理,把每个证明都搞明白。
给分:期中141+期末100=总评100,我在科大拿过的最高的分数,也算对得起这学期的努力。
总之,这门课为我打开了对微分方程认知的大门,也激发了我对微分方程的兴趣。感谢赵老师一学期来的认真教学和助教们的辛勤付出!
- 课程难度:困难
- 作业多少:中等
- 给分好坏:一般
- 收获大小:很多
- 难度:困难
- 作业:中等
- 给分:一般
- 收获:很多
强烈建议改成6学分课程
计算量无敌大
一定要自己动手算
不然就像我一样, 考试寄了......
赵立丰真的奶王,zlf我的超人!
- 课程难度:困难
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:中等
- 给分:超好
- 收获:很多
老师和助教都超级好!
这门课的内容还是很多的,前半学期学ODE后半学期PDE,课时有限,不少内容都略去没讲,但还是很多。
ODE部分还是不难的,一部分定性理论一部分解方程。给你一个方程,你要能判断是哪一类方程,然后用相应的办法求解。定性理论主要是解的存在唯一性和动力系统平衡点分类。
期中考试比较简单,基本会算就行,六道还是七道解方程,后面一半考定性理论,其实还是计算。(比如动力系统平衡点那块,你要知道那个点的稳定性,就要算对应矩阵。)
后半学期PDE可就难多了,在此提醒同学们:
大一下的向量分析一定要学好!!!
不然你只能看着满黑板的nabla算子和积分号不知所云。这部分学起来会比较吃力,做作业会比较困难。(我经常写作业得重新看两遍书和笔记本,不然动不了笔。)最后考前重新看了一遍笔记本,发现思路还是比较清晰的。
好在最后考试很简单,送分从头送到尾,没有难题。(虽然我还是有一问智障了没做出来。)
总评99,还是有一点遗憾,当初期中拿了很高的分数想着这门成绩会不会成为我的第一门三位数,结果期末考差了那么一点,算是学PDE没有学到家的报应吧。
最后表白三位助教,水平好负责任,爱死。
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:很多
微分方程I,好神奇啊!
记得当年学的时候还囫囵吞枣,背完笔记就算成功没有任何时间消化,结果不出意料学得一塌糊涂,总评甚至比wffcII还要低好几分。。。学完之后很长一段时间对这门课也没啥印象了。
倒是刚刚这个学期学的内容最近又让我重新回忆起这门课。比如随机微分方程里的(局部)lip条件用picard迭代run一遍接存在唯一性,durret ch9讲了从概率论视角解古典PDE几个模型,可以看作是简单的ito积分的应用(找到合适的鞅就行),现在看了点点gaussian free field,感觉其中通过SRW构造的green function也非常神奇,看来概率论与PDE的联系还真能催生出有趣的数学问题,可惜自己基础实在太差了。。。
学完PDE感觉基本上要么拆括号(分部积分+holder),要么造轮子,而这恰恰也是深奥的学问,可惜自己对方程没有任何感觉。
当时赵老师应该是第一次带这门课,虽然节奏很赶,但还是把技术细节及其想法大部分都讲得很清楚,考试题出得很有水平,最后确实让我寄得心服口服。记得当年考试题计算量不小(不过听说近两个学期考试都放水了),大家学得也挺好,感觉还是自己的问题。。。
下学期还得三开PDE,永世轮回批地易啊!
- 课程难度:困难
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:中等
- 给分:超好
- 收获:很多
感天动地zlf!!!!!!!!!!
微分方程不能赵老师,就好比不能没有耶路撒冷
老师水平真的是非常非常高!!上课十分的精彩!!
会把证明背后的动机和构造函数思路告诉大家,而且比较难的课课后会把讲义发到群里面。
期中考试和课本贴合度很大,考了老师强调了非常多次的Nullcline.
自己期中认真复习拿到了137分,因为最后一题伪证了还不自知..期中总共考了2h45m(15m是后来延长的),总体来说不是很难。个人感觉ODE部分比较容易(可能是学的太少了?)
到了PDE...画风突变,,,自己学不会了qwp
被PDE苦苦折磨了半个学期,考前复习了三个星期(我太菜了对不起呜呜呜),好不容易感觉自己稍稍理解了一部分...然后被期末考试无情打垮。
期末本来说考两小时,赵老师延长了25分钟。感天动地啊!!不过我考完还是赶紧自己完了qwp
考后出分惊讶无比!!居然满绩了!!!期末比自己预计分数高了将近二十分!!!
总之,选爆好吧!!!
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:一般
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:一般
由于这学期课程作业太多,前半学期实在没花多少时间来学ode,再加上自己计算能力卜太行,半期考试空了二十多分没写,满脑子只有:
还好期末放了水,计算量小(第一题分离变量法还是没算出来),考题比较常规,用的套路基本上是上课讲过的,认真复习问题就不大。最后总评貌似有期中期末取高的操作所以期中炸了影响也不大?实在是
感天动地赵立丰。
三位助教认真负责,基本上每周都有习题课,讲义的内容也很充实,同时还考虑到团建活动,有的同学不能来五教参加习题课,于是采用了网上直播录像的形式。然而我去了习题课也没怎么听,而是一直在写其他课的作业,实在惭愧
关于PDE,其实可讲的内容很多,但赵老师并没有讲太多枯燥的定性理论和需要过多升级知识的复杂证明,而是在课上简要介绍了研究方程的各种方法,让同学们有一个简要的了解,可以说是在不给学生太大的压力同时,也在想办法提起大家对PDE的兴趣,同时也坚定了自己quit的决心。
10分!
- 课程难度:困难
- 作业多少:很多
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:很多
- 给分:超好
- 收获:很多
赵老师yyds。
从个人角度讲,或许是数分A2学得还行(雾),所以感觉PDE部分反而比ODE简单一些。
赵老师的考试非常非常偏重于上课内容,所以不听课是不行滴(震声,期中血的教训,,)
其它方面,学长们说了很多,我就不补充了。
给分:期末100+直接将我费拉不堪的期中带起飞,,,感谢赵老师给我在妮可的第一个满分总评。
更新:毕业一段时间之后回头看看,我认为这门课是本科最‘有用’的数学课之一,只因微分方程是普适地存在于所有的数学中的。一切泛分析学科(包括了传统分析方程、几何、概率、数学物理、应用数学)中涉及到连续时间演化与精细估计的问题,全部要回到这个视角,或是从其中寻找灵感。我至今仍然经常遇到当时学过的问题,惭愧自己学得太差。
- 课程难度:困难
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:很少
- 给分:超好
- 收获:很多
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:很多
课程内容
整个课程分成两部分,前半学期常微分方程,后半学期偏微分方程。常微分方程大致分为求解和定性理论两块。赵老师基本是照着教材讲,一些打星号的定理只讲结论省略证明,一些关键点会加入部分自己的理解。由于微分方程I这门课本身在课程安排上的不合理性以及本学期教学时间的紧迫性,教材第八章的极限环和第九章的Sturm-Liouville理论讲得比较粗略(S-L理论是在PDE讲分离变量法的时候介绍的),但赵老师能介绍这么多内容已经做得很出色了,个人感觉听赵老师讲比自己看教材体验好很多。
偏微分方程是赵老师的本行,主要讲了三类方程的一些求解方法和基本性质。由于这部分的上课时间只有不到一个半月,考试时间又比较早,赵老师和大家商量后把课程增加到每周五学时以便提前结课,给大家更多的期末复习时间,可以说是相当贴心了。不同于往年的是,赵老师选择了谷超豪校长的《数学物理方程》作为主要教材,没有选择Evans或者Strauss,但在一些结论的证明上采用了Evans上的方法,同时椭圆方程部分选择了按照韩青林芳华的第一章讲授,个人认为这种尝试非常好,回避了Evans上一些对初学者不太友好的内容(如heat ball,一般维数的波方程求解),丰富了椭圆方程部分的内容,把韩青林芳华书上省略了很多细节的证明讲得非常清晰。当然讲得清晰不代表你听过一遍就会了,很多东西还是要亲手算一遍才能真正理解。
关于考试
期中考试考ODE部分,题量较大,计算题基本涵盖了讲过的各种解方程的方法,证明题包括了Lyapunov稳定性、奇点分类以及利用延伸定理和比较定理证明存在性。个人认为Picard存在唯一性定理的证明思想挺重要的,可惜在考试中没得到体现。
期末考试考PDE部分,题量不多,两道计算三道证明,包括了分离变量法和Fourier变换求解方程,波方程解的依赖区域和决定区域,Green函数的性质,次调和函数的“拟平均值性质”(这个词是我编的hhh)
总体上赵老师出题比较常规,基本都在课上(包括习题课)和作业中有所体现。
关于给分
好得超乎你想象
总的来说非常推荐赵老师的微分方程I这门课(据说下一届开始要课程改革了,以后可能会叫数学物理方程)
最后附上赵老师推荐的一些后续参考书:
ODE部分:M. Hirsch, S. Smale, R. Devaney, Differential Equations, Dynamical Systems & An Introduction to Chaos, 3rd edition
T. Sideries, Ordinary differential equations and dynamical systems
G. Schneider, H. Uecker, Nonlinear PDEs, A Dynamical systems Approach. Part I
PDE部分:Serge Alinhac, Hyperbolic Partial Differential Equations
韩青,林芳华, Elliptic Partial Differential Equations
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:很多
赵老师是搞pde的,水平巨高,讲课也很到位,尤其是pde部分换教材之后,在讲定理证明的时候会把动机和证明过程都说的很清楚,很容易理解并应用,庆幸开学初换到了这个班。老师水平给十分,助教水平给10分。 扣一分在课程内容,ode讲的十分浮光掠影,内容也很少,定性理论少之又少(不过赵老师算好的了,隔壁班听说一点都没讲)。pde部分的设置还是不错的,把最简单的三类方程讲了一遍,也涉及到了证明的一些操作,将来pde2应该也会用到很多。 总之十分推荐,看到赵老师选他的课准没错。
修改一下评分 9变10。赵老师绝对值这个分数!
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:很多
赵老师的讲课内容和风格不再详述,可以参见其他高赞回答。
对于大多数人来说,这是一门全新的课,也是之前没接触过就无法吃老本的课。
像老师所说,每节课都能接触一些新的东西,新的方法。方程相比于淑芬、线代等基础课学起来会感觉有一点点玄学,经常会遇到许多神奇的操作与构造,但老师总在努力地把所有的动机和想法讲明白,让我们接受得更快一点。
上课还会有些不舒服的地方可能是,赵老师在写大篇的计算过程时对于初学者来说很快,而且还会边写边擦,好像老师不是很喜欢把自己的草稿留在黑板上,但那些计算所用的公式和技巧却正是我们在自己读书学习时难以想到的,所以一定要尽量跟紧老师。一定要知道每一步操作用到了什么,记下来用它的动机和想法,而不必在老师做计算时把每一步完全想得清楚明白,验算是必要的,但在知识没有透彻掌握之前不要在课上做,以防漏掉很多东西。
ODE部分技巧性比较强,从看起来最简单的解ODE到稳定性李雅普诺夫函数的构造都需要用到一定的技巧,这一部分在初学时会感到困难,但是老师可能只要求让我们掌握方法,所以考试题目完全是上课所讲方法的简单应用。
这门课的PDE部分只讲了波方程、热方程、位势方程最基本的一些性质,用老师原话来说,学完这门课的PDE最基本的要求就是会解方程,所以期末考试中,相对于相对于位势方程的Green函数求解(事实上容易解的仅仅是半空间,二维和三维球),波方程的分离变量法(非齐次方程和初值很重要),相对于热传导方程的Fourier变换(考试前一定要把e^(-x^2)的Fourier变换背下来,并熟悉使用方法,这门课从头到尾见到的Fourier变换题目没有不用这个公式的,但这却好像没有被强调过。当场用解ode的方法推可能可以,但要知道,解出这个函数的Fourier变换只是题目中的一小部分,直接记下来会省很多时间)也成了“最基本也一定会有”的题目。但即使提前知道了,计算是个大问题。
剩下的PDE的各种精妙的性质,老师上课讲的很明白,但是在老师讲完后一定要亲自动手验算过,并尝试着联系点物理意义去理解它们存在的意义。这里可以除了老师给定的教材,通过阅读不同的参考书去弄明白感觉玄学的性质。PDE部分的作业题基本是对所学方程性质的简单应用,稍有复杂的构造在作业和考试中也都给出了充分的提示。从考试题也中可以看出,热方程、位势方程的最大最小值原理是最需要掌握的部分,也是最典型最有代表性的性质。
总的来说,学好这门课最需要的是花时间,花时间把上课听懂没听懂的部分自己算一遍,平时写作业和总结时认真把一步步证明和计算写出来,花时间去把多变量微积分练熟(求导的乘法法则逆用,也对应着分部积分,格林公式,散度定理等,具体可以自己刷一遍EVANS的附录相应部分,其实效果最佳的可能是刷一遍相应正文,在自己尝试填补书上的计算gap时,对于符号和相应计算自然而然就熟练了)。不要怕花时间,学习过程中,每天课下拿两个小时去算PDE是值得的,而不是“低效”。
贴一个期末复习时把老师给出的框架填充了一下下的版本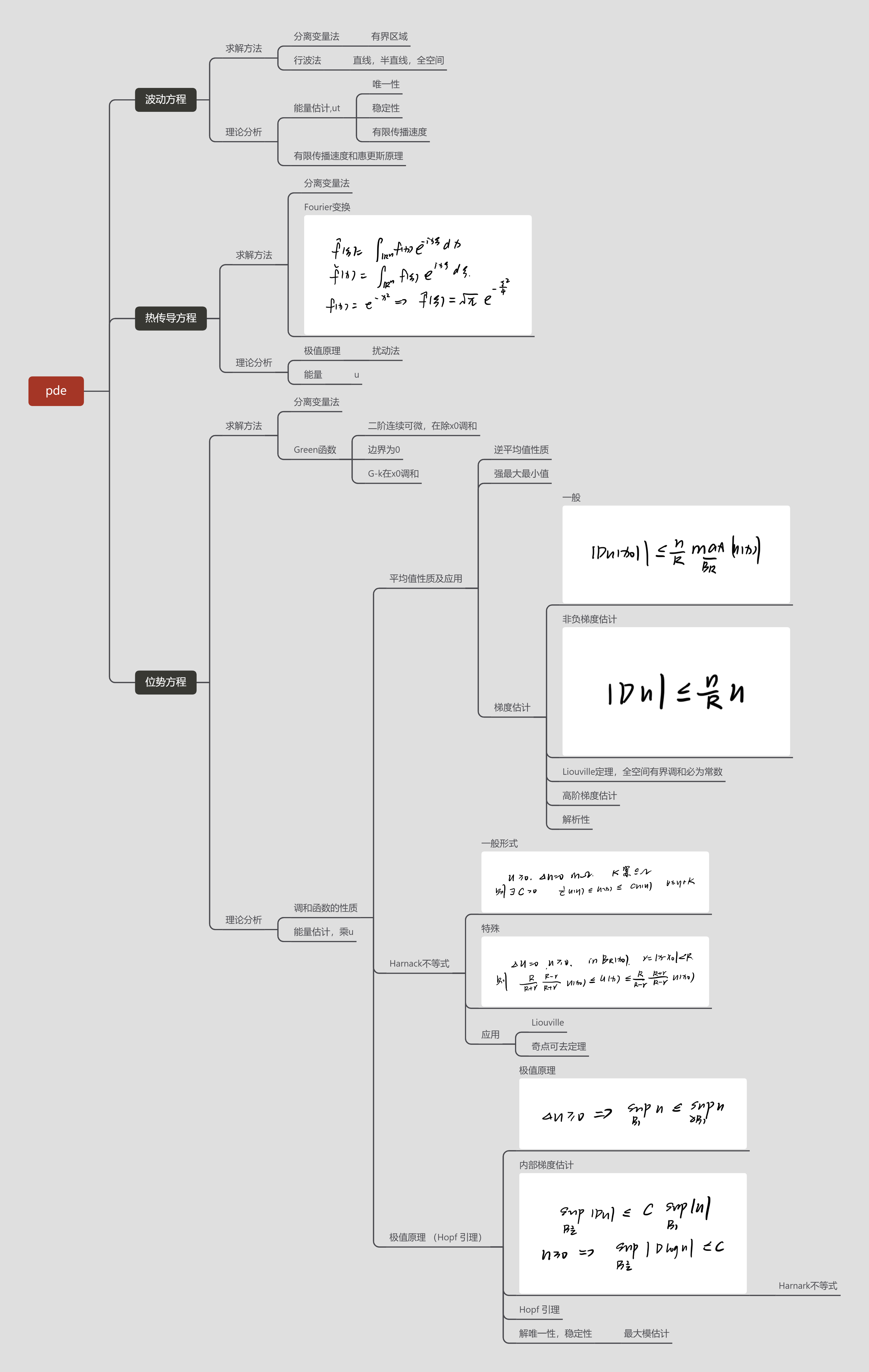
- 课程难度:困难
- 作业多少:中等
- 给分好坏:一般
- 收获大小:一般
- 难度:困难
- 作业:中等
- 给分:一般
- 收获:一般
赵老师非常擅长把简单的定理讲复杂(尤其是偏微分方程),上课和笔记就是不懂,看课本就明白了。我建议选宁吴庆老师的班,因为赵老师的班选的人太多了,大佬多卷的人也多,给分也不如想象的那么好。
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:很多
赵老师比“能量法”更yyds! ①讲课: 老师讲课超级清晰,每节课开始会用几分钟回顾一下上节课的内容。 上半学期ode和2020年内容基本一样。个人感觉内容比较多,所以复习很重要。习题课也是。 下半学期pde教材是陈祖墀(chi)。讲的和教材不完全一样,老师建议大家记笔记(虽然每节课都会发讲义)。用的所有方法都是以前没见过的,内容比较多,但不是很难理解(老师说的)。 最后一节课老师推荐了四本参考书,有一本是Stein的傅立叶分析,据说这是Stein自己最满意的的一本。 老师人很和蔼,长得喜庆,非常认真负责! 三位助教小哥哥人都很好,改作业和讲习题课超级认真! ②考试: 期中考试满分150,难度正常(老师说不难),最后一题考了零解稳定性证明,很多人犯了数分里的低级错误从头就开始错(孩子只得三分)。 期末考试满分100,个人感觉比期中简单。赵老师出题向来比较“正常”,有区分度又不会离大谱。有一道原题(圆盘green函数),其他的思路也都见过。 ③给分: 只能用yyds来形容。我期中122,期末96,最后总评95,给分比实际水平高太多了T_T看群里大家的反应,应该给分都很好。 得了大学第一个4.3之后点飘,来评课社区写篇流水账,由于水平太菜就不写关于数学的部分了。最后墙裂推荐赵老师的微分方程引论!
- 课程难度:困难
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:中等
- 给分:超好
- 收获:很多
课程确实比较离谱,塞得东西很多。期中考试ODE卷子不错,期末PDE的卷子稍微有点离谱,强调的Hopf引理Harnack不等式梯度估计一个没考,倒是前面的计算出得比证明难。不过老师确实很捞人,所以总体还是很推荐。
- 课程难度:简单
- 作业多少:很少
- 给分好坏:超好
- 收获大小:一般
- 难度:简单
- 作业:很少
- 给分:超好
- 收获:一般
老师很好,给分很好,pde部分感觉东一榔头西一棒槌不能串联(?)
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:很多
这门课的内容很多,上学期ode加下学期的pde,是这学期选的数学课里花费的时间能排得上第二的课,但其实这门课并不算难,但就为了赶进度一些地方讲的比较快也就不是很深入,但对我这种一般不去上课(我才不会说是起不来床)的人影响不是很大,ode里的稳定性讲的比书上多了不少内容,但多读几本别的教材搞明白稳定性还是不难的,期中考试很简单,就是送分的计算题加上几道难度中等的证明题,但由于没去上课所以不会画什么nu线再加上奇点判断错了最后只有139,不过也算比较满意了,期中之后的pde刚开始学很难,但计算可以找本数学物理方程的习题做,理论部分可以多读几本教材,理解了之后就会觉得蛮简单的了,一些比较难搞的理论比如球面平均法什么的可以不用管,反正估计期末也不会考 这门课最大最大的不足就是学分跟学时严重不匹配,甚至还要把幂级数部分放到习题课讲,强烈建议四学分改成5-6学分!!!
老师很奶!!期末爆炸2,3都算错了最后分数80出头还能调上4.3!!
- 课程难度:中等
- 作业多少:中等
- 给分好坏:一般
- 收获大小:一般
- 难度:中等
- 作业:中等
- 给分:一般
- 收获:一般
占坑
老师很好很耐心,你随时可以去问他问题。
助教也很nice。
- 课程难度:困难
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:中等
- 给分:超好
- 收获:很多
感天动地赵立丰!
感觉是大二上最难的一门数学课了,学的感觉很吃力,但是老师上课还是挺好的~
最后考试感觉做的很糟糕,数分考试时都做好3.3的准备了,结果考完一看有4.0!!!奶王!!!
zlf是我大爹!
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:很多
大家都来选赵老师的微分方程啊,真的是一门很好的课,内容是半学期ode与半学期pde,课程内容还是比较丰富的。我本壬ode部分学的稀烂,导致期中直接爆炸,pde部分的话感觉还行,就是很多学的东西不知道怎么落到实处,就比如波方程的有限传播速度,不会用啊,,,哎也许还是太菜了。
给分方面的话感觉期中期末占比应该不会差太多,期末稍微考好了一点点勉强拉上了3.7,给分方面的话见仁见智吧,总体上应该还是很不错的。
- 课程难度:困难
- 作业多少:中等
- 给分好坏:一般
- 收获大小:一般
- 难度:困难
- 作业:中等
- 给分:一般
- 收获:一般
课程内容太多了!PDE太难了!整个学期18周就要学习几乎整本《常微分方程》与几乎整本《偏微分方程》两册书!后期基本上听不懂,只能死记硬背一些结论。不过老师和助教都很nice!
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:一般
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:一般
这门课分为两个部分,前半学期ODE(教材是丁同仁),后半学期PDE(教材是谷超豪),由于课时限制ODE部分讲的不多,甚至将幂级数解法放在了习题课,PDE部分的话,老师本人是做PDE的,感受到老师高超的水平,讲的也很到位。具体的课程内容介绍我就不说了,交给大佬吧。
老师还是很关心学生的,我没记错的话是每次习题课都在后面随堂(在后排刷着手机的我一回头和老师对上眼神XD)。助教也很nice,习题课讲的很好,答疑回复很及时,课后都会上传讲义,巨大好评。
有关考试和给分,说实话老师还是很亲民的,本人期中暴毙,期末考完以为自己凉了,看到助教给出的总评之后脑子里只有一句话:感天动地赵立丰。这都能奶活,太狠了。
闲扯两句吧,这门课的作业很少(至少这学期如此),可能老师是想让我们把精力放在理解课堂内容上,所以课后还是要花一些功夫的。确实如果分部积分和散度定理学的不行的话,PDE课上很容易懵逼。其他的话,只要课上认真一点,考前爆肝复习,问题不大吧,考试的话老师关于理论部分的考察还是比较简单的, 毕竟这门课对于大多数同学的要求还是掌握计算即可,往往考的不好很可能是计算能力方面不过关。
最后的bb:求求了,换掉谷超豪吧,那上面各种记法真的接受不能XD
(有时间的话我会上传自己PDE课上的笔记,前提是我能找到
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:很多
老师本身是研究pde的,水平巨高;我们这届助教也不错,平易近人。 说课程本身,ode方面限制于课时,真的讲不了多少,主要还是靠自己课外巩固,老师和助教都非常尽力地想要带我们领略ode的美妙之处;pde方面,课本这玩意只是用来布置作业的,老师上课讲的真的很精彩!!!!!助教在习题课拓展的部分也非常有用!!!!!!任何一节课(包括习题课)都不能旷掉!!!!!! 然后就是考试和评分,两场考试对于大佬来说不成问题,对于普通学渣(比如本人)来说真的难到心态炸裂,最后喜提期中期末考均不及格的“好成绩”(都没过均分)结果总评还有2.7!老师调分力度真的很大!
总结:老师教的好,助教也好,学的很多,学不会的同学也不一定挂科。
- 课程难度:困难
- 作业多少:中等
- 给分好坏:超好
- 收获大小:一般
- 难度:困难
- 作业:中等
- 给分:超好
- 收获:一般
好难啊这门课😭😭😭微分方程II都比它容易😭😭😭我好垃圾😭😭😭
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:很多
老师很好,很负责,听老师上课听的很爽
- 课程难度:困难
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:中等
- 给分:超好
- 收获:很多
选课前听说赵立丰老师很奶,出分之后发现果然很奶
课程内容含量较大,包含ode和pde的一大部分内容,建议改为六学分(bushi)老师上课还是挺有条理的,各个定理的证明相对清晰,并且课后会给出上课的讲义,花费一定的时间还是可以理解的。
助教也是很负责的,有什么问题线上问助教都会熬夜解答(bushi)平时习题课也会补充一些内容(当然对期末考并不一定有用,但是能加深对内容的理解)
课程作业量不算大,有的周题目比较阴间就可能需要花费大量时间,有的周相对较好。期中考和往年的题目较为相似,这次期末考题目量大,对计算要求不高,主要考察对讲义中证明方法的理解。笔者期中表现不佳,但期末还行就被赵老师大力奶起来了
总结一下,极力推荐赵老师,赵老师yyds
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:很多
在赵立丰老师班上分析水平提升了很多!
给分也真的很好!
考试没有太为难人
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:很多
其他的前面的同学说的很全面了。老师真的挺善良的,作业大概是大二上三门必修课里面最少的,而且后面怕我们写不上来还布置了教材里的定理。
卷子出的也比较简单,期中一直说要考的Picard迭代的相关证明没有考,卷子上都是作业里讲过的方法(以及课上讲过的原题),往常卷子里会出的一道利用群的性质去做的压轴也没有。期末更是非常基础,有两个书里的定理,我完全没搞明白的截断函数的构造就完全没涉及,甚至简单的辅助函数的选取也没有考。真考了怕是只能空着了QAQ
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:很多
老师上课思路清晰,而且给人一种很亲近的感觉。
水平很高。让我们可以沿老师的思路理解一些抽象内容,就没有那么吃力了。
给分很好,好的要怀疑人生了。
很喜欢邵助教上习题课。金句频出。
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:很多
今年的评论,看楼上几位大佬就好,都是实话
我废话不多说,直接十分
感天动地赵立丰!
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:很多
我就不多说了,感觉楼上的大佬分析介绍得很充分了。
总之,赵立丰老师和三位助教非常棒,配得上这个十分。
- 课程难度:困难
- 作业多少:很少
- 给分好坏:超好
- 收获大小:一般
- 难度:困难
- 作业:很少
- 给分:超好
- 收获:一般
关于上课内容其他点评已经说得很清楚了,我就说说作为一个分析基础不是那么扎实的人的感受吧,前半学期ODE部分老师基本上按书(丁同仁《常微分方程》)讲,所以勉强还能跟上;后半学期PDE老师并不完全按照书上讲,而是有自己的节奏,导致跟上有点吃力,但是前几天复习的时候看着自己的笔记发现老师讲的确实很有条理,也确实看出了老师的专业水平扎实,助教也都很认真负责,习题课也准备的很充分,尤其是sf助教的习题课尤为精彩。只可惜我这学期也要兼顾其他课程,而且我对方程也没有过多的兴趣,所以并没有在这门课上过多花时间,也有点辜负了老师和助教吧。给分方面应该挺好的,期末卷子改的松,而且调分力度也挺大。总的来说,如果赵老师以后还开微分方程1的课,选就是了。