2023春 2022春 2021春 2020春 课程号:MATH300102
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
| 选课类别:计划 | 教学类型:理论课 |
| 课程类别:本科计划内课程 | 开课单位:数学科学学院 |
| 课程层次:专业核心 | 学分:3.0 |
教材:冯克勤《近世代数引论》
参考书:Thomas W.Hungerford: Algebra, GTM 73
课程内容:教材
- 课程难度:困难
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:中等
- 给分:超好
- 收获:很多
今天考完期末,这门课也刚好出分了,来详细点评一下。
张磊老师以往一直带代数几何和黎曼曲面这种升级的研究生课,没怎么带过本科生课,所以选的时候其实有各种方面的担心。比如怕老师把握不好本科生课的讲课进度,或者给得不好,像去年xjx一样给分杀的天昏地暗。不过一学期上下来之后感觉各方面体验还是很好的。
张老师平时上课用classin手写板书的形式,讲的内容挺多,把欧书的所有内容都涵盖了,还补充了一些模的内容。讲的还是很不错的,虽然说老师第一次带这门课有些地方进度把握的不是特别好(比如Sylow定理那一块感觉实在太快了,听了若干遍后才懂了一些敢上手写作业题),而且在classin系统上翻页的速度太快导致跟着记笔记经常记不完。不过总体而言思路很清晰,而且比教材通俗易懂很多。每次看教材看到实在看不懂的地方翻回看录屏都能很快弄懂。期末复习我也基本上没看教材,而是看平时上课记的笔记。
不过就我个人而言,近世代数是一门非常非常困难的课,难度远超同学期上的复分析和实分析。当然这个因人而异,我个人认为自己学代数课没啥感觉,两学期线性代数收获了主课的两个最低分,而且还没有上过大一上的代数学基础。再加上教材写的十分精(quan)简(tui),习题也不好做,导致在学的过程中受到了很大打击。当然估计很多同学也同样觉得吃力,张磊老师学期中特地给我们喂了一碗“鸡汤”来鼓励大家,给我的启发还很大的,虽然改变不了我被这门课打击的事实。建议跟我一样代数基础不怎么样的同学在学这门课看一些英文教材(比如rotman,dummit),那些书“废话”比较多,对初学者友好一些。对于作业题,也不用去太过于较劲,实在不行去近世代数300题上找答案。就算自己没想出来,如果能把它的做法记下来,收获其实也很大的。
这学期有一次期中考,期中在线上考,开卷,而且题目比较简单(平均分估计80)。期末考试也是放了洪水出卷,没有出任何技巧性强的题目。前面五选四的40分和后面Galois那题20分中的18分都几乎完全送分。但期末考试据说成绩还是不高,平均分刚刚及格(不过查完卷后很多人都加了不少分)。
最后给分老师是调了分的,按照平时期中期末334的比例来给,算是给的不错了。我自己这门课拿到的分也比之前两学期线性代数拿的高一些,已经很满意了。
最后还是把老师的鸡汤放上来

- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:很多
2023春学生,如果2024春老师还带可能会是助教(已和张老师说过)。
罗列一下这门课的重点(其实就是讲义的title)。
一.群论
子群,陪集(Lagrange定理),阶,循环群。
正规子群,商群,同构定理。
群作用(典型的例子左乘,共轭),Sylow定理。
自由群(注意泛性质),群表现。
有限生成自由Abel群。 有限生成Abel群结构定理。 小阶群分类。(8阶群,学有余力可以试试12阶群。)
二.环论
子环,零因子,单位,除环,域,整环
环同态,理想,商环,生成理想
环同构定理,特征,中国剩余定理,素理想和极大理想,分式域
整除与相伴,不可约与素元
UFD(三个等价性质),和PID的关系,ED
多项式环,UFD上多项式环的因子分解(本原多项式,Gauss引理)如何判断不可约元。
三.域扩张
(回顾:根的重数,Eisenstein判别法,不可约和极大理想的关系)
有限生成扩域,单扩张,超越元,代数扩张,超越扩张,有限扩张
(有限扩张是有限生成扩张,有限扩张是代数扩张,有限生成的代数扩张是有限扩张有限扩张的复合有限,代数扩张的复合代数)
代数闭域,代数闭包
有限域
--------------------分割线----------------
感觉这门课张老师上得很平易近人,(虽然我有仏班基础学过前面的群论,所以觉得不难),作业也比较基础,考察理解,有仏国遗风。虽然zl不调分但事实上最后优秀率还是打满了,强推。
助教之中,bkc爸爸对于袋鼠的理解很深刻,w17写习题讲义很尽职尽责(虽然我就偶尔看两眼不会的题顺便挑挑错,但是17真的顶),助教丙感觉高深莫测。
而且老师也很可爱,表情包很多。



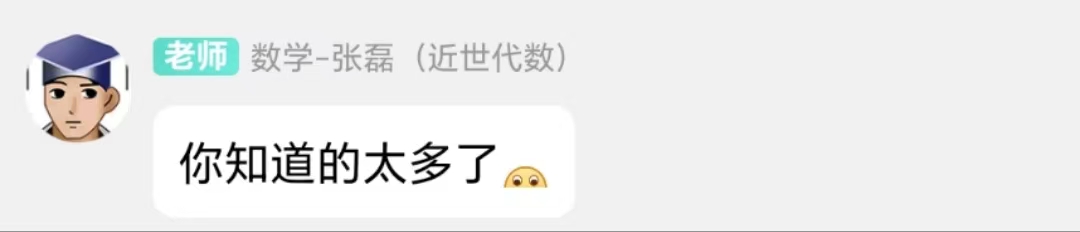



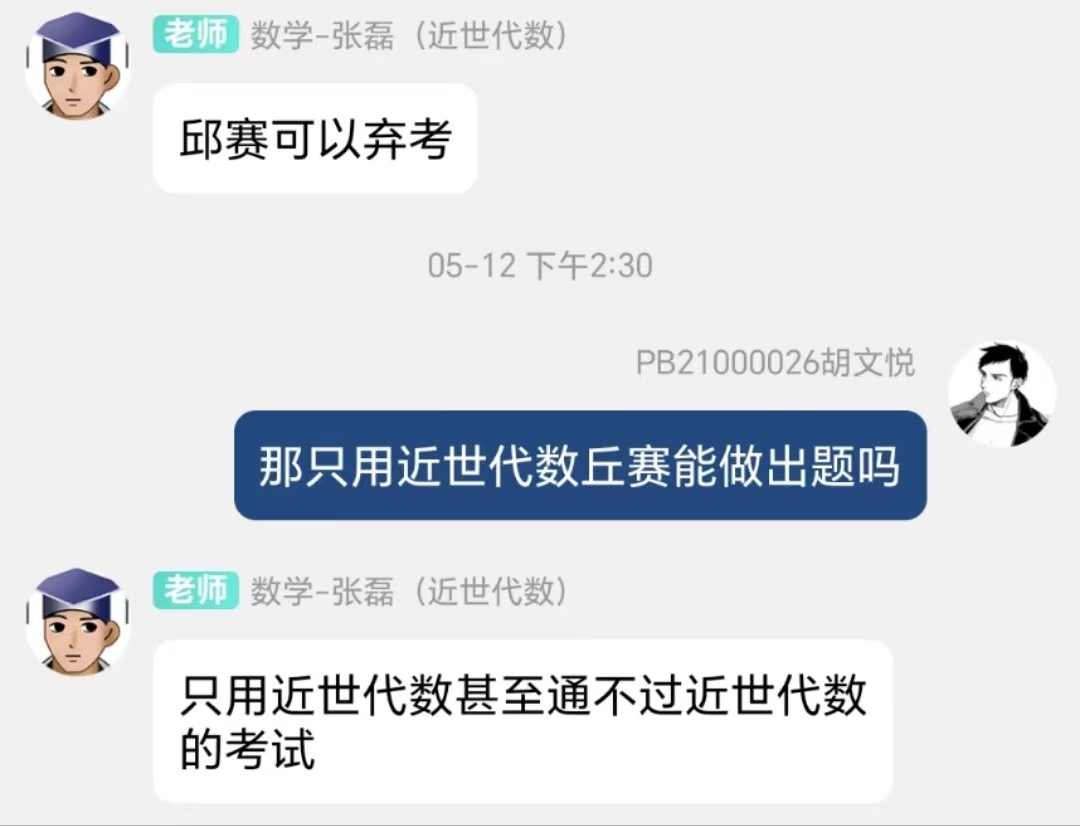
- 课程难度:困难
- 作业多少:中等
- 给分好坏:一般
- 收获大小:很多
- 难度:困难
- 作业:中等
- 给分:一般
- 收获:很多
这篇评课的后半部分是作者一时兴起写的随感. 想了解课程信息的读者可以直接略过不看.
----
(2023.07.17)
内容简介
教材主要分为三个大的章节: 群论, 环论与域论, Galois理论.
这门课不讲Galois理论部分. 今年域论好像也没有讲完 (或者说考试没有要求) , 有限域以及后面的一些部分似乎没有在考试题里出现.
·
讲课
关于张磊老师讲课的描述可以见后半部分的随笔.
这里补充一点: 张磊老师上课证明定理的时候喜欢不作准备, 当场推演, 结果时不时会出现证不出来的情境. 有趣的是这种挂黑板的情况并没有对授课带来障碍, 反倒让人觉得很亲民, 自己课下学习遇到困难时的心理压力也低了不少.
·
作业&考勤
作业题量不多不少, 难度上每次会有几道题需要深入思考. 不过这门课作业直到考试前都允许补交, 助教17还会每周收完作业按时更新答案. 所以实际上做不出来抄一遍交上去都行. 在此也再次mod17.
前几个星期点过名. 点名的目的据老师所说 "是为了认识一下同学" , 所以是按照名单上的学号顺序点的. 我的学号是11开头, 直到结课似乎也没有被点到过.
·
考试
期中题比较基础, 除了用到Sylow定理的一个小问都比较简单.
期末题综合性很强, 判断题的坑性就不用说了, 每道大题也时常需要在群论与环域论的知识之间跳转.
我期中92/100, 排名大概是前1/3处; 期末没太考好, 90/105, 排名反倒高了一些, 两张卷子的难度对比可见于此.
·
学习
这门课我自己学的时候比较吃力, 学习方法分享什么的就不献太多丑了.
课本是冯克勤 <近世代数引论> 第4版. 我因为此前自学代数结构的时候买了丘维声的书, 不想再买一本太重复的, 就白嫖了一个学期课群里的电子版 (不知道为什么扫出来字是很淡的灰色, 看一个学期能把人眼睛弄瞎) . 教材评价的话, 如果说隔壁 <代数结构> 是0分, 一本及格的教材是60分, 丘书是80分的话, 冯书大概介于及格与丘书之间 (当然也可能是因为我一开始用的丘书, 习惯影响了体验) . 看书自学的效果远不如听老师讲课.
张磊老师提到过我们班的作业与考试题难度都略低于三百题. 我想把这门课学好点, 于是两次考前都是以刷三百题的方式复习的. 从做题后的感觉来看, 刷三百题的作用并不主要在于能为考试卷多少分, 而是对理解知识有很大的辅助功能. 许多泛用性很高的简单推论 (比如子群的交还是子群, 含幺环) 都在三百题里被出成了证明题. 这些命题单独作为一道题拿出来让人证可能很容易, 但在做比较综合的题的时候, 初学者就很难自然地想到利用它们.
·
----
(2023.05.06)
刚学完群论, 还没期中考. 就自己目前的感受随便絮叨一点, 想到什么写什么 (以后会补通用格式的评课) .
2022年春季学期, 作为计科大一生的我修读了作为计科专业基础课的代数结构. 了解一点计科课程及对应风评的读者大概知道: 离散数学三部曲在计科向来是不受学生欢迎的存在, 其中又以代数结构为甚, 计科人们大多给其打上 "抽象" "复杂" "不说人话" "没有用处" 等标签. 与主流的情况不同, 我在学习代数结构的前4章时便感到十分有趣, 在接触到了群环域后更是惊叹于它们的美, 并 (很自然地) 对抽象代数产生了兴趣. 然而, 代数结构教材粗浅的知识与贫瘠的洞见显然不能满足一个学习者对知识的渴求, 而那时的我对本科数学学习也几乎没有什么了解, 不知道该去哪里寻找进一步的课程. 幸运的是, 从代数结构班上一名同学的只言片语中, 我听说了数学系的 "近世代数" 课程, 也产生了将来选修这门课的念头. 2022年秋季, 在图论课上的得心应手更使我觉得自己对 "抽象" 的数学分支有某种天赋, 也更坚定了我下一年选修近代的念头.
时间来到2023春. 开学时通过叠两对课+在课表上排华容道, 从计算机转大数据的我如愿以偿地在安排好了专业必修课的同时, 还能往课表中加进 "数理逻辑基础" "近世代数" 两门自己感兴趣的课程. 上近代课的实际体验与我当初的预期既有吻合也有不同. 符合预期之处在于的确接触到了许多更精彩的数学概念, 定理与思想: 自由群, 对有限生成Abel群的洞析, 如此等等都使我惊叹于几百年前的数学大师的洞见与巧思. 预期之外的部分可分为积极与消极两部分. 积极的地方在于有意料之外的发现: 数学系的学习方式与计科的是如此不同, 并且完美地符合我所理想的模式 (关于这点后文会详谈) .
消极的部分则可想而知: 近代的知识分支虽然与代结基本吻合, 但在广度, 深度与难度 (这个词有些宽泛, 更合适的说法或许是 "抽象程度" ) 上则远超后者. 而这种难度迅速地将我对自己所谓 "天赋" 的认知击得粉碎. 在其它课程中我当然也有过完全学不明白, 或者卡在某个证明的经历. 但那些情况要么出现在复变, 必修物理等自己完全不关心的课程或章节中, 要么也能在足够长时间的思考后逐渐找到能够说服自己的解释 (比如计科图论中连通性的一章) . 相比之下, 在学习近世代数这门本以为很适合自己的课程时, 自己竟然前进得举步维艰, 这对我实在可谓是一个巨大的打击. 我不得不学着接受并习惯于这样的情况: 每周的作业即时迟交也有一半的题做不出来, 做出来的那些也被助教指出的漏洞或伪证之处戳得千疮百孔. 偶尔在为作业中的必做题冥思苦想的同时, 我也会苦笑着用 "对数院学生来说或许也一样难吧" 这样的话安慰自己, 内心深处却始终难以接受自己水平不够的事实.
回到今天上午的此刻, 量子物理复习不下去的我打开电脑敲着这篇更像是杂文的评课, 不禁回想起去年今日那个在代数结构课上意气风发的自己. 尽管近代的难度十分劝退, 我依然认为选修这门课给我带来了重要, 乃至无可替代的收获, 无论是在知识之内还是之外. 而后一种收获或许甚至超出数学系的教授们对课程功能的预设. 正如前文所言, 选修的第一门数学课让我认识了数学系的学习模式, 而这种模式与我此前所设想的应有的学习模式十分吻合:
计科的许多专业虽然都与数学有所交叉 (例如程设进阶, 数据结构, 以及大数据的数据库) , 但在原理讲解上要么不做作要求, 要么一带而过, 要么只给出一个正确但 "诘屈聱牙" 的证明, 等着学生自己 "开悟" . 与之相应, 学生群体也无形中形成了排斥思考数学的观念, 认为研究方法背后的数学原理要么是大佬的闲趣, 要么是傻子才会浪费时间去做的亏本买卖. 这也使得我在遇到感兴趣的问题时往往没有可以讨论的同伴, 难以得到数学学习的体验. 像近世代数这样一门不仅对现实几乎没有应用 (其实就我所知在密码学中是有的) , 连对数学的其它常见分支也没有什么贡献的课程, 放在计科恐怕是最不受待见的一类. (就连张磊老师半真半假地承认 "近世代数没用" . ) 而为了学懂近世代数 (直白地说, 哪怕是为了能做出考试题) , 花大量时间反复咀嚼知识中的洞见又是必需的. 这种让大多数计科学生唯恐避之不及的过程, 与我而言却是享受, 甚至是计科课程枯燥无味的学习中唯一能给自己带来一点慰藉的时段. 这或许是因为所谓 "洞见" 大概算得上我眼里最为美丽之物, 而数学专业的学习在这点上恰好与我一拍即合. 这常使我想起Halmos在他的自传中所写:
"Don't just read it; fight it! Ask your own questions, look for your own examples, discover your own proofs. Is the hypothesis necessary? Is the converse true? What happens in the classical special case? What about the degenerate cases? Where does the proof use the hypothesis?"
时至今日我关于自己将来的去向仍旧犹疑不定, 不知是该在计算机或大数据继续走下去, 还是该考研时转去读数学. 但无论哪种情况, 我都愿意将这钟在近世代数学习中养成的思考与钻研的习惯保持下去.
最后闲聊几句关于老师和助教: 由于我不知道数学系老师讲课的模式如何, 无法评价张磊老师讲法的特点; 只能将其与此前遇到的计科老师的风格作比, 简单地说老师对证明中的洞见作了尽可能详细而平易近人的剖析 (当然这在数学专业课的教学中可能是很常见的) , 而不仅仅是抄书或复述一遍书上的句子 (计科的许多老师还真就这么讲课) . 至于助教, 我所在组的助教反馈风格可谓至简, 迅速而有效: 每次私聊交完图片版的作业, 都能很快地收到对作业中证明错误的指出, 除此之外很少有多余的话. 这样的说话方式或许使有些人觉得难以相处且 "没有人情" , 但很符合我对学习交流的预期. 尴尬的是我一直不知道这位助教的名字, 只能用其群昵称 "助教丙" 来称呼学期末评教的时候知道了.
- 课程难度:中等
- 作业多少:很少
- 给分好坏:一般
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:一般
- 收获:很多
6.23改:出分了。之前写的废话太多,自己现在看着都不好意思,删一些。
老师和助教以及课程本身都很优秀,前人之述备矣,所以五颗星雷打不动。
本人大一先修,同级巨佬大多数都去选隔壁H课了。提前选修的无外乎下面几类同学:
(1)自身实力超群,并且对近世代数感兴趣;
(2)对课程内容早已通晓,为以后选课腾出时间;
(3)其他(作死类)。
本人属于第三类,能力显然不超群(线代濒临挂科),也不可能通晓近世代数内容。
扯远了,回到正轨上来吧。。。
教学顺序是:群论全部——期中——环——域——域扩张,期中只考群论,期末以域扩张、有限域为主。
群论学习建议:(本人环论和域论学得很不扎实,没资格提建议)
群之非凡者三:群作用,Sylow定理,自由群。群作用若只看一本教材可能比较懵,然而本人亲测,把两本相差较大的教材的定义与例子比较着看,那么理解起来会轻松得多(比如冯克勤《近世代数引论》和丘维声的《近世代数》)。Sylow定理过于长篇大论,然而只要把《引论》上的定理1,即“对任意素数p和正整数r和有限群G,只要p^r整除G的阶,那么G的p^r阶子群的个数模p余1”这个结论把握好就OK,而且这个结论更强,同时也能顺便把群作用理解得更为充分。自由群方面,建议(最好根据老师讲解)把Dn的群表现搞清楚,由具体到抽象地理解。
说一下自己考试的体验,今年普班近代改成了3学分,15周每周两次两节课的时间(我们22春还因放假掉了好几次课为什么被冲的不是大雾实验),一学期学完压力比较大(据本人了解许多学校是两学期讲完抽代)。因此期中题目格外友好,(希望期末出题手下留情)而且期末大放水,然而不知为何两次平均分都不高。本人期中93(大约20名),期末85(大约25名),按照334差不多正好是总评92。期末因为偷懒跳步在严格的阅卷下被扣了5分(谈不上痛失4.3,即使加上也摸不上边)。个人认为高分段给分非常好,因为卷子实在太简单了,况且我这样的菜鸡期末考完了之后还傻傻地在群里问艾森斯坦判别法怎么用,期末还把直和与直积搞混了,还算出来2的三次方等于6都能被捞到4。
推荐明年学习近世代数的同学选张老师的课!
- 课程难度:中等
- 作业多少:中等
- 给分好坏:一般
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:一般
- 收获:很多
本人是22春该课的助教,,来小小锐评一下
虽然我感兴趣的方向也比较偏代数,但确实觉得该课程内容不是非常吸引人。因为是近世代数的入门课程,其课程内容只能是一些比较基础的概念,可能会让很多同学觉得内容繁复枯燥,很少有深刻奇妙的结论,事实上我早年学的时候也是如此,,可能也因此学代数的同学都比较少。
当然解决这个问题的方法就是多了解一些具体的例子,从例子出发理解每一个定义和命题才能感到其合理之处,并且有直观的感受,而不会觉得这些概念抽象需要死记硬背。(例如一开始学群论可能会觉得是抽象的数学小游戏,但其实在其他数学领域甚至物理中会发现群论最重要的部分是群作用,或者说对称性的刻画,在这之中正规子群,共轭等概念就会有比较具象的理解)因此张老师的课上也讲了不少书上没有的例子和相关计算,我习题课也试图补充了一些(讲了一些用群作用定义商空间的例子,多项式环的几何观点之类的)
但自己去查找所需要的例子对大多数同学并不容易,一方面中文教材经常写的过于简练缺少动机和直观,一方面很多例子需要其他领域的知识储备(比如几何、数论)。所以建议觉得上课讲的/教材写的难以理解的时候可以翻翻有名的英文教材(Rotman,Artin等等),不用从头看直接看对应章节就可以,,
这门课还有一个基础和重要的部分就是要把定义和证明写明白,,比如期末考试有个送分题证明ℤ[x]/(x^2+7)同构ℤ[sqrt(7)i],我改的时候似乎只有不到一半的同学写出了定义这个同构的映射,,这种同构在环论和域论里还是比较基本和重要,还是要记得吧。事实上这门课的环大致也只有整数环的“有限扩张”和多项式环的商这两类,(对应数论和几何)建议把基本的计算搞明白。
今年是第一年改3学分,,我的评价是出发点很好而结果不尽人意,,去掉Galois对应感觉也没让大伙轻松多少,反而对域论其他必考知识的理解不够到位了,考试的时候一个简单的域论题目也扣分比较多。我还是觉得应该尽量减少必修课,减到只有数分线代(暴论),毕竟对于很多同学学习60学时的近世代数几乎对其以后没有用(80学时的pde2也是如此,),纯纯的折磨学生,,
最后还是,如同前面说的,该课程内容只是代数的基本语言,更多深刻有趣的观点/结论可以在后续课程(作为近世代数的应用)看到,比如代数数论,交换代数,群表示论,代数几何等,学习更多知识后对该课程里的内容应该也会有更立体的理解,
给分应该是334算总评没怎么调(至少高分段),应该是因为高分段也比较多吧
- 课程难度:中等
- 作业多少:中等
- 给分好坏:一般
- 收获大小:一般
- 难度:中等
- 作业:中等
- 给分:一般
- 收获:一般
被捞了,给17和磊子磕一个 明天裸考完线性代数再评
学完这门课算是与代数做一个告别了,没有不舍,只有愉快(bushi)
强推张磊老师的近世代数
1. 张磊老师讲课非常清晰,而且讲课内容大多不难,听课感受很好。难的没听所以不知道啥感受。
2. 老师布置作业量不多不少,而且允许迟交,今年17写了一分作业答案而且允许迟交,所以期中之后作业都是等着17写完答案我直接copy,所以做作业从来没心态爆炸过,不和某些分析似的,每周作业抄不懂,不会写,写的想紫砂。
3. 张磊每周会发笔记和作业pdf,虽然不是很详细,但是是一个提纲,有助于对整体学习内容的把握。
如何准备考试?
想学好这门课的请移步其他大佬的评课,我学的不好,但是考的还好
有必要看三百题吗? 我的结论是除非4.3否则没必要,我反正没翻过
有必要看往年卷吗? 我的结论是除非4.3否则没必要,我反正没看过
有必要听习题课吗? 其实我也没去过,但是和助教多多交流绝对会有很多帮助!
我自己的复习基本平时就是听个课,每周课下的时间大约用半个小时左右稍微看看学了啥,等到所有课程结束之后基本上也不大会啥,期末复习大概就是先把所有作业抄完答案补交,还剩两三天的时候把课本重点知识整理了一遍(整理的时候只整理了重点的证明,其实过了一天就忘了),之后作业中的感觉比较重点的题目考前过了一遍,常用结论整理了一遍背了好几遍,过程中遇到不会的就直接甩给17然后17光速解答(磕头),耗时也就两天左右,考前只会背结论证明都忘光光,但是期中期末都90.
也算大二最后一门专业课,虽然学的不咋好,但是感觉只要把握住课程的主要结构和主线这门课就能考的差不多,一些繁杂的细节很缠人,但是,毕竟不是学代数的,搞清楚这门课的主线才是最重要的,细枝末节作为喜好看看就好(反正我不想看)。
哦,还有期末考试的 (mod 17) 下跪,磕头,直身,再磕头!
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:很多
期中占坑
今天出成绩了,分布很恐怖,近乎指数分布,不幸的是,我排在靠后的位置
感觉近世代数一直学的不明白
后续有待期末补充
7.25出分了,由于我期中倒数,最后总评只有83,很可惜
期末很简单,基本上没有为难大家的题目,最后总评公式据说是25 25 50,然而这样优秀率好像还是超了(
有个小插曲,期末考试的时候流鼻血了(,很担心自己写不完,结果zl正好延长了半小时,好耶!
后半学期和前半学期相比感觉更加适应了zl的讲课节奏,而且再复习了一边前半学期的内容之后,感觉并没有那么抽象
十分建议大家选择zl的班,你会收获一学期的快乐课堂
最后表白助教17,一学期的相处下来,17相比于助教,更像是朋友,他会为我们解答题目,为我们疏通心里问题,而且几乎时刻在岗,问问题几乎秒答,在另外两位助教不准备习题课讲义的情况下,他甚至写了一份所有作业的答案,他真的我哭死。
- 课程难度:中等
- 作业多少:中等
- 给分好坏:一般
- 收获大小:一般
- 难度:中等
- 作业:中等
- 给分:一般
- 收获:一般
四学分改三学分, 难度不高, 老师讲的很好, 最后因为期末少写了几个字, 痛失4.3.
最后334 貌似一分没调.
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:很多
老师很好,推荐大家来选
希望大家都做一个好学的人2333
- 课程难度:困难
- 作业多少:中等
- 给分好坏:超好
- 收获大小:一般
- 难度:困难
- 作业:中等
- 给分:超好
- 收获:一般
偶然想起之前做了个九宫格,在这里也放一下:

压线3.7,太感动了!
由于A1被wxm杀了,我A2润到了叶先生班。期末又被背刺,叶先生只给了我3.0,于是这学期就没往叶班换。现在来看,确实是个极其正确的选择。
本来打算最后一门代数课混混就过去了,于是期中月、期末月的时候,经常上课双线程,一边记笔记一边复习其他的,掉队了不少。后来概率论寄了,我只能靠近世代数给救一下,期末考前才开始补天。多亏zl的板书清晰、内容友好,以及助教高度完备化的答案,我才能勉勉强强给这门课理出一个脉络。
期中过于简单,导致了U型分布,期末难度也不是很大,于是按比例算出来——优秀率超了。
改算分公式后,算出自己77分可以拿3.7。然后一问分:76。(当场心肺骤停)
后来多亏17助教帮我从仏式大题中查回3分,侥幸3.7。
这应该是zl第一次给满优秀率(也可能超了)。
zl应该是我选过最好的代数老师了,没有之一。虽然以后就没有代数课了,还是很感谢zl能给我这么好的体验。
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:很多
老师讲课很好,把近世代数这门课讲得很有趣,即使程度不太好的同学也可以跟的上并且学到东西。
最难得的是老师对待同学的态度,非常非常亲切,没有架子,就像对待同学朋友一样。
有一段时间老师总喜欢点名,因为想认识更多的同学,避免在路上碰见打招呼的学生叫不出名字。
有时上课大家累了老师会分享自己的小故事,调节一下氛围,可以感受到老师对生活很有热情。
老师鼓励大家不要太看重成绩,大三了真的没办法不看重,压力很大,期末考的很差,去查卷,见到老师有点惭愧,老师还像对待朋友一样热心地讲解了每一处错误,才发现原来老师真的不看重成绩,只关心学生有没有把知识理解到位。
老师给分很奶,虽然考砸了,总评还是奶到可以接受的范畴。
都说近世代数很难,有老师领着学起来并没有很痛苦。
总结:课很好,老师很有人格魅力,给分很好,十分推荐。
- 课程难度:中等
- 作业多少:很少
- 给分好坏:超好
- 收获大小:一般
- 难度:中等
- 作业:很少
- 给分:超好
- 收获:一般
老师上课节奏较慢,学的很舒服,17助教超有趣,每次习题课都很快乐233333(17讲解K4的生成关系:怎么可能是三个元素,他们仨都地主去了谁管它呢)。适合普通班对代数不咋感兴趣,浑水摸鱼得过且过的人选。
- 课程难度:简单
- 作业多少:中等
- 给分好坏:一般
- 收获大小:一般
- 难度:简单
- 作业:中等
- 给分:一般
- 收获:一般
删掉了Galois理论的讲解,三学分的课程内容显得有点无聊,如果对代数感兴趣的话还是应该多看一点课外书籍,gtm73、gtm211的域论Galois理论我认为是合适的参考书。另外我认为代数的学习还是需要多做些习题来加深理解,gtm73以及张老师出的补充题都是不错的习题。(先做张老师的习题,有多余时间和精力的话可以做做gtm73的习题),具体的计算是有必要的,光看抽象理论容易沦为cjb(当然天赋异禀的话另说)。考试考察的内容比较基础,我考的不错,给分是平时期中期末334,别的不做评价。 张老师人非常和蔼可亲,有任何的学习上的问题和想法都可以向老师询问,他都会耐心解答。张老师还寻求创新,讲有限abel群结构定理的时候说想到了不同参考书上的更加简洁的证明,我在其提示下仍然思考了很久做不出来,最后在和他argue的时候发现果然是他伪证了,,,然后他也很快在课程群里面承认是自己想错了,,,
- 课程难度:困难
- 作业多少:很多
- 给分好坏:一般
- 收获大小:一般
- 难度:困难
- 作业:很多
- 给分:一般
- 收获:一般
可能是我最后一次学代数课了,代数学不懂,但不妨碍给张磊老师打高分。
张磊老师的课是十分平易近人的,适合看不懂书只能期望把课堂内容基本理解的咸鱼,老师的讲课方式也是和大家一起从原点一步一步走向知识深处。这门课也一样,即便完全没有其他课的基础,用张老师的话说,有了小学知识,便可以理解,听起来是玩笑话,但仔细想想在一定程度上确实如此。代数学基础,线性代数都不怎么会的前提下,上课专心听讲,把笔记全部抄下来下来仔细看几遍,也能理解老师讲的大部分内容。数学是需要反复学反复重复的,一遍看不懂,可以一天看一遍。做到这种程度的话,作业依旧是十分困难,虽然题目个数也不是特别多。到了后期就是用几个小时想再用几个小时把答案看懂抄上去的感觉,也不知道学会了啥。记得最艰难的几段,便是早上起来吃过早饭开始做近世代数作业,直到晚饭前才大概把答案看懂,不能理解深意。学习的过程中我也和不少同学和学长聊过,这门课到底应该怎么学,学过之后到底有什么用,也没有得到除了认真听讲做笔记复习之外的答案。
曾经听到过一个说法是近世代数这门课对于其他方向的同学完全没用,我认为有一定道理,但数学专业不学抽象代数还是有点说不过去。可能对于大部分以后不会从事代数相关研究的同学,这门课的定位就像是一个科普,让我们大概了解数学中最抽象的东西可以抽象成什么样,不同结构之间可以建立怎样神奇的关系,等到学期末,也不用要求太高,能自己画几个不那么简单的交换图出来,写几个同构,这门课的目的也就差不多达到了。老师对这门课的定位大概也是这样,不要求所有人学得多深多透,题目很多,也有很多选做题,感兴趣就做做,不感兴趣就算了,也没啥必要。考试也是如此,基本功扎实至少不会太差,涉及罕见技巧的题目完全不会也没事,作业抄一遍答案就够了。
张老师是一个比较纯粹的人,对于同学们的关心和对于所从事研究的热爱有目共睹,听说和他交流可以学到不少东西,社恐的我没有主动去和老师聊聊也有点遗憾吧。但这自然的也会有一些点,不能让所有人满意。如果你介意拖堂,介意卡绩点的话,张老师的班也许就不是最优选择。
当然,所有以上所讲是基于我自己,一个学不太懂代数的人的想法,也给和我有相似情况的学弟学妹,尤其是学习代数学基础和线性代数A系列与同时间其他数学课程相比感到极大困难一个参考。对于擅长或者热爱代数的同学,以上全是废话,不必多看。
- 课程难度:困难
- 作业多少:很少
- 给分好坏:杀手
- 收获大小:很多
- 难度:困难
- 作业:很少
- 给分:杀手
- 收获:很多
可能因为这学期改成三学分,两个老师都没仔细讲最后一章,也的确没考,老师出题还算比较放水了,两极分化过于严重(底子好的人比较多),讲课中规中矩,没啥特点,但是如果不会的话一定不要想着看讲义,因为老师讲义比较粗略,甚至会删掉一些不太重要的东西(但是我个人感觉这些遗漏对内容理解还是很有影响的,所以我都是靠自己笔记和书本复习),复习的时候我都是看隔壁讲义的,平时不点名,作业题也没有完整答案(隔壁作业多但是有全套答案,这件事见仁见智吧),习题课不听也没什么问题(反正考的和习题课没什么关系)。
至于给分,334,平时分作业交了就给满,根据一些同学的反映,优秀率大概率没给满,卡绩无论卡多少分也基本没怎么捞,也有部分人要补考,用老师自己的话来说,不要太在乎成绩,总结起来就是全靠自己,没有加分项,也没有减分项,你要是底子扎实,不需要听老师讲课靠自己考试就能拿高分那选这个班没什么太大问题,隔壁老师讲得很多,很细致也很快,就是作业太多,但是最后微调把优秀率给满了(隔壁的高分段实在太多),所以取决于你自己感受
虽然我觉得我对自己分数比较满意,但是我个人感觉今年给分对初学者还是挺不友好的,毕竟今年一般来说有四门数学硬课,如果没有一定的基础,这门课还是很折磨的,期中的时候老师只给了80分以上的人数,下面的老师说给了会制造焦虑,之后上课的人就越来越少了,老师呼吁过同学们来上课好几次,但是人数的确肉眼可见的变少了,平时群里讨论问题的人数,相比于这学期其他的课程的确太少了。只能说期中和平时课程难度很大程度上使得一些人放弃了这门课,混了个通过就不想再学了,同比于这学期实复分析,概率论,这门课难度过高,给分也的确不如另外三门,但是高分段比例却远胜其他三门(只能说这就是近世代数的特色:会的人轻描淡写,不会的人备受折磨)
- 课程难度:中等
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:中等
- 作业:中等
- 给分:超好
- 收获:很多
不可多得的好老师,如果再加上本学期的三位助教,简直完美!
每节课后老师都会上传讲义,讲义除了证明细节较少外都很详细,复习时看讲义足够了。助教的习题课准备很充分,答疑很快。
唯一的遗憾可能就是Galois理论只讲了一节课(可能是这门课由4学分改为3学分的原因吧)还是希望能多讲点这部分的内容(所以还是希望这门课能改回4学分)。
给分:334,不调分,本人期中98,期末87,总评正好94。没什么可说的,还是自己期末太烂了,痛失4.3,但作为一个大一少院人已经满足了。
- 课程难度:困难
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:中等
- 给分:超好
- 收获:很多
张磊老师人非常好,对同学非常亲切,就像对待朋友一样。
老师上课讲的非常细致,并且经常会在线上给同学答疑。
考试的话,期中和期末都很基础(难度低于作业选做题),正如老师所说,他不喜欢出技巧性强的题目,所以建议先把课上讲的内容多看看,300题是个比较好的参考题集,把基本内容理解透了以后可以参考一下300题。
强烈推荐大家选张老师的课!
- 课程难度:简单
- 作业多少:中等
- 给分好坏:超好
- 收获大小:很多
- 难度:简单
- 作业:中等
- 给分:超好
- 收获:很多
感觉卷子有点太简单导致最后是在拼细节,我就是考场上忘了两个公式导致拿了4😭
- 课程难度:简单
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:简单
- 作业:很少
- 给分:超好
- 收获:很多
张磊老师我吹爆
昨天考完最后一门,正好有时间写一下课程评价。近世代数这门课还是很基础的,主要内容就是群环域和Galois理论。受限于课程时间,张老师只讲了Galois基本定理,没有讲它的一些应用,不过张老师把他的笔记发到了课程群中供大家自学。如果想要在这门课上获得一个好成绩还是需要对这些内容有一定的理解。张老师给分的规定很严格,但是也很好,我期中考的比较差但张老师还是给了我一个不错的分数。
关于上课,张老师一般会先回顾一下上次课的内容然后开始讲新课,我感觉十分不错。张老师上课也是十分有意思,每次上课之前张老师都会在课程群里发消息提醒大家来上课。张老师留的作业不多,有些题是选做,不做也没关系,不过做了应该对学习有好处的。
总之,张老师的课非常好,建议都来选
- 课程难度:困难
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:很少
- 给分:超好
- 收获:很多
正如楼上所说的,老师真的是很好。期末查卷一个题一个题帮你分析错误之处和他的打分标准。老师的绩点有严格计算标准,因为分数刚好卡在某个节点,导致我要分时和老师有不小的争论。在我情绪激动的离开后,老师还给我发消息。哎,真的真的特别惭愧。
对于近世代数这门课,我觉得是极难的,虽然老师讲的很清晰很有条理,但在上群作用时,我体会到了”前面每节课都认真听,结果新的一节课完全听不懂的“的感觉。在此之后,近世代数对我就成了折磨。不过虽然如此,就考试而言,近视代数是少数的不需要技巧题、只通过考察对基本概念的掌握和简单应用情况就能有区分度的数学课,而老师也直言他不喜欢出技巧题。所以在一轮复习了解基本概念、解题套路后,其实近世代数某种意义上来说反而是比较轻松的。
正如老师所说的,近世代数定理证明每一步都是平凡,但结合在一起就是极不平凡的。在考试主要考察的内容里(不包含伽罗瓦),虽然我多数时间被折磨到吐,但现在回头来看,我觉得只有群作用、sylow定理那里是不平凡或者说是tricky的,其余的环、有限域其实都蛮平凡的。但另一方面,也许是我不擅长学代数吧,我觉得近世代数的平凡却是极难的,就像老师的期末期中考,虽然出的很简单,但我却会犯很多错,有些平凡的关系我也很难一下get到,甚至对于我,相较而言,我其实对cxw老师的那些套路题更有把握。
至于参考书,我觉得期中(群那块)刷300题,但也不必把太过计较于那些难题,学些思路就好(比如小阶群的分类),考试肯定出的比它简单。期末(环以后)300题意义不大,看书本把书本定理与部分课后习题弄透其实更好。
- 课程难度:困难
- 作业多少:中等
- 给分好坏:超好
- 收获大小:没有
- 难度:困难
- 作业:中等
- 给分:超好
- 收获:没有
代数实在是太难了
数感不好的学代数犹如学语文,不要理解它,尝试接受它。
作业导向型学习,复制完作业回头背一背解题过程。
在学懂程度不及20%的情况下靠着往年卷的原题惊险拿到了4+
- 课程难度:简单
- 作业多少:很少
- 给分好坏:一般
- 收获大小:很多
- 难度:简单
- 作业:很少
- 给分:一般
- 收获:很多
老师人不错讲课讲的很好,但是不调分有点顶
- 课程难度:中等
- 作业多少:中等
- 给分好坏:一般
- 收获大小:一般
- 难度:中等
- 作业:中等
- 给分:一般
- 收获:一般
关于课程:近世代数难度还是挺高的,尤其是最后讲到域扩张那边的时候,想要上课跟上压力都很大。因此比较建议提前预习。老师很和蔼,也很有意思,有时也会水群。同时,张老师上课讲的很细致,也很流畅,每节课后都会更新讲义,每周也会有习题课,老师和助教们都是相当负责的。 关于作业:包括书上的题和补充题,一周差不多十道左右,作业量和难度都比较合适。 关于考试:期中考群,期末是25%群,50%环,25%域,虽然课程难度比较高但考试却相当友善,基本都是上课讲过的内容,最难的域扩张也只考了最基础的部分。 关于给分:目测是334,然后纯四舍五入,不调分。
- 课程难度:困难
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:很少
- 给分:超好
- 收获:很多
张磊老师真的是很好的老师,其他同学已经说得很详细了。
这门课对我一个不是很开窍的人来说难点主要有这些
1.申必的蓝色薄教材,西罗定理和群作用那一部分看的迷糊。
2.宽松的作业政策,有选做题,阅读题,作业可以一次性补交不扣分。(不过考试难度低于选做题和阅读题)
3.可能是这门课的特点,张磊老师讲课经常会提起之前说过的结论,然后没有预习复习习惯的我后半学期与环的映射有关的我就上课跟着老师笑一笑,课下再看了。。
比较后悔后半学期没怎么认真学习,以至于后半期作业是一次性补交上去的,直到了考试的前头突击,才发现域扩张理论的美妙之处(从定义的代数,超越扩张的概念推出域同构,推出根与最小多项式的关系,自然的导出代数闭包与分裂域的概念等......)。
但老师的给分很不错,0.3平时+0.35期末+0.35期中(变动后),把我成功捞起。如果实在不想看英文教材的话,近世代数引论应付考试已经够了。
- 课程难度:困难
- 作业多少:很少
- 给分好坏:超好
- 收获大小:一般
- 难度:困难
- 作业:很少
- 给分:超好
- 收获:一般
超高校级的幸运
改天详述
来了:D
张老师人非常好。热心回答问题,上课态度认真,照顾有困难的同学。隔壁班的机油还来答疑蹭了一题hhh
虽然不像syh会弄出latex讲义,但是手写了讲义供我们使用。个人觉得这份讲义虽然内容平实,但条理清晰,面面俱到。在我看来,数院本科生基础课并不需要去拓展许多(这门课尤其如此),而更应该讲好课本的、大纲上的内容。故这份讲义是很适当的。第一次在科大带本科,张老师稳定控制了课程的难易度和进度,也没有为了炫技而整一些花活,是很难得的。
上课的时候,经常能听到张老师说,【啊这里我那会儿第一次想也想不出来,后来逐渐思考,才掌握了。】比起syh那种自信的腔调,这令我很心安。
课程的内容基本和蓝皮教材一样。我自己对这本书的评价要高于不少同学,仁者见仁吧。虽然如此,还是建议翻翻p大的书(一般p大书讲的比科大书要“稳”一些,适用于各种数学基础课。),再翻几本外国教材(如大佬们常说的Rotman),主要是完善知识体系和拓展看问题的角度,不需要细致阅读。近世代数课无论谁来上,都不会是一门软课,多看些书是有好处的。300题是好材料,给我们展示了这门课解题时的思考角度,对应试和理解知识很有帮助。
和教材不一样的是:张老师补充了PID上有限生成模的理论,并且给出了一条清晰的路来完成结构定理的证明,作为非考试内容。这倒是我感兴趣的地方,算是给自己线性代数A填坑吧。
这门课的观点将数学中“一般化”的思想体现的淋漓尽致,这一点十分吸引我。然而像我这种水平是不可能学好这种课的。。。
由于疫情的缘故,划了很久的水,考前一直在跟机油请教问题,想能补救一点是一点。如果按照往年那样考我必死,结果最后成绩也很意外,超高校级的幸运。。。不过我是觉得,这门课(非H)的考题,技巧越少越适当。
题外话:选张老师的课其实是为了避开syh。
上面有大佬发了张老师的鸡汤。这里附一张图。印象中我那阵子作业题根本憋不出,进度跟不上,就跟老师诉苦,结果居然得到老师这么长的回复。想必已经有不少同学找老师聊过了,当周老师就在群里发了上面的那份鸡汤。感动。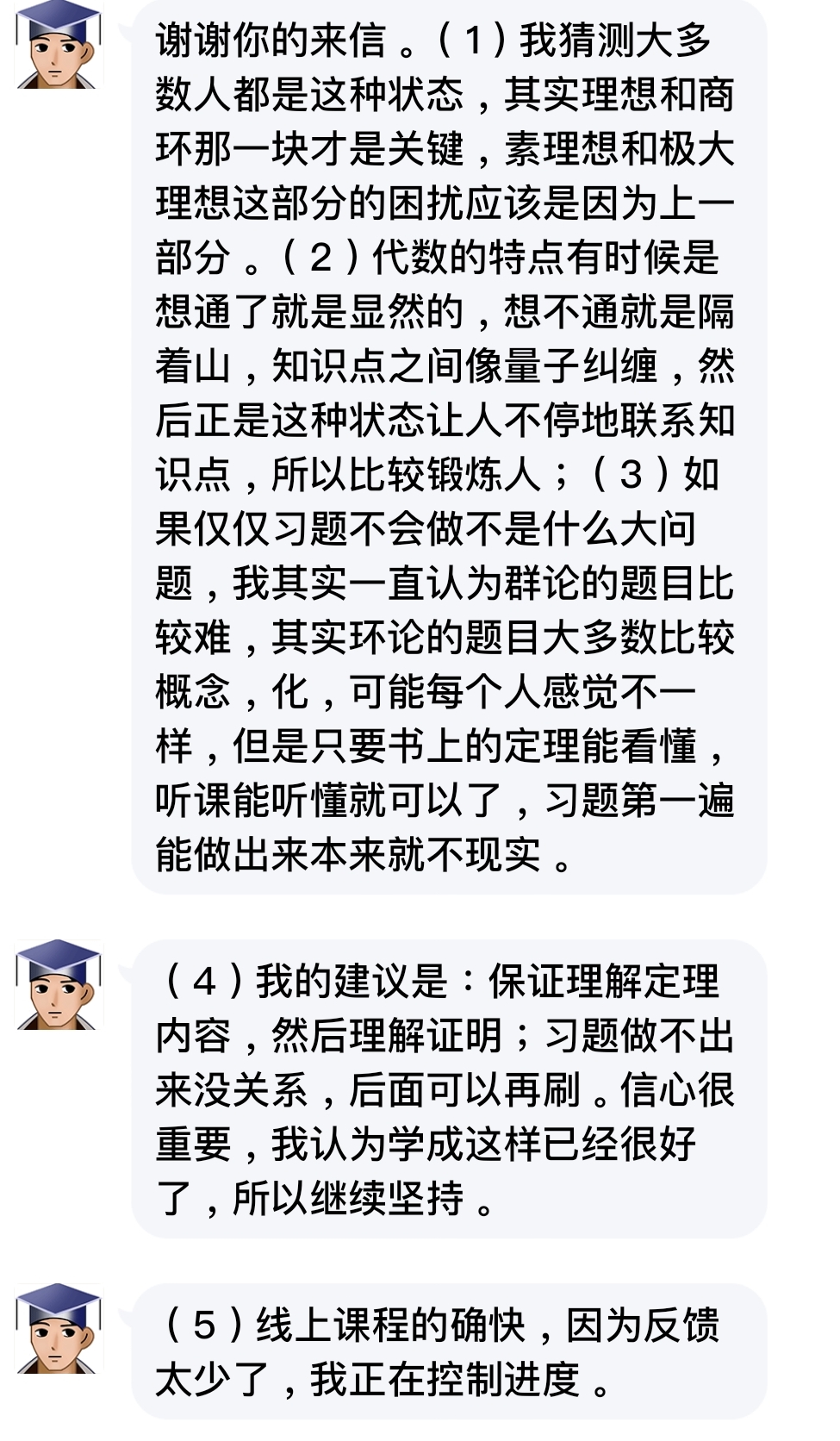
- 课程难度:中等
- 作业多少:中等
- 给分好坏:一般
- 收获大小:一般
- 难度:中等
- 作业:中等
- 给分:一般
- 收获:一般
张磊老师人很好,备课很认真,还时不时和学生交流,写写鸡汤什么的;考试还能整点活什么的。